அளவைகள் | இரண்டாம் பருவம் அலகு 2 | 7ஆம் வகுப்பு கணக்கு - வட்டத்தின் சுற்றளவு (Circumference of a Circle) | 7th Maths : Term 2 Unit 2 : Measurements
7ஆம் வகுப்பு கணக்கு : இரண்டாம் பருவம் அலகு 2 : அளவைகள்
வட்டத்தின் சுற்றளவு (Circumference of a Circle)
வட்டத்தின் சுற்றளவு (Circumference of a Circle)
அனைத்து வட்டங்களும், ஒன்றுக்கு ஒன்று வடிவொத்தவையாக உள்ளன. ஆகவே, அதன் சுற்றளவுக்கும், விட்டத்துக்கும் இடையேயான விகிதம் எப்போதும் ஒரு மாறிலியாக உள்ளது.
அதாவது, சுற்றளவு/ விட்டம் = மாறிலி [ π( pi ) என்க ]
ஆகவே, C/d = π இதன் தோராய மதிப்பு 3.14 ஆகும்.
விட்டம் என்பது ஆரத்தின் இரு மடங்கு (2r) என அறிவோம். எனவே, இந்தச் சமன்பாட்டை C/2r = π. என்றும் எழுதலாம்.
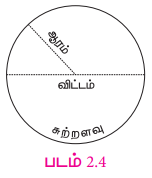
இவற்றிலிருந்து, வட்டத்தின் சுற்றளவுக்கான சூத்திரம் C = 2 πr அலகுகள் என அறிகிறோம்.
இப்போது, வட்டத்தின் சுற்றளவு C = π d மற்றும் d = 2r என்று அறிவோம். எனவே எந்த வட்டத்திற்கும், கொடுக்கப்பட்ட 'r' அல்லது 'd' இக்கு, நம்மால் C காண முடியும். இதேபோல், C கொடுக்கப்பட்டால் ‘r’ அல்லது 'd' ஐக் காணலாம்.
உங்களுக்குத் தெரியுமா?

1. π இன் தசம மதிப்புகளைக் கண்டறிவதில், கணித அறிஞர்களிடம் பலத்த போட்டி நிலவுகிறது.
2. உலகப் புகழ்பெற்ற எகிப்து பிரமிடுகளின் கட்டமைப்பில் π என்னும் மாறிலி பயன்படுத்தப்பட்டுள்ளது.
3. கணிதவியலாளர்கள், கணினி உதவியுடன் இதுவரை 12 லட்சம் கோடி (trillion) தசம மதிப்புகளுக்கு மேற்பட்டு π இன் மதிப்பைக் கண்டறிந்துள்ளனர்.
சிந்திக்க
சமப் பரப்பளவுள்ள அனைத்து மூடிய உருவங்களிலும், வட்டம்தான் மிகக் குறைந்த சுற்றளவு உடையது. இக்கூற்று உண்மையா எனச் சோதித்து அறிக.
எடுத்துக்காட்டு 2.1
படம் 2.5 இல் உள்ள வளையலின் சுற்றளவைக் கணக்கிடுக. ( π = 3.14 என்க)
தீர்வு
கொடுக்கப்பட்டது, d = 6 செ.மீ, ஆனால், d = 2r = 6 செ.மீ, r = 3 செ.மீ

வட்டத்தின் சுற்றளவு = 2πr அலகுகள்
= 2π × 3
= 18.8496 ≈ 18.84
எனவே, சுற்றளவு 18.84 செ.மீ ஆகும்.
எடுத்துக்காட்டு 2.2
ஆரம் 14 செ.மீ உடைய வட்டத் தகட்டின் சுற்றளவைக் காண்க. ( π = 22/7 என்க)
தீர்வு
வட்டத்தகட்டின் ஆரம் (r) = 14 செ.மீ
அதன் சுற்றளவு = 2πr அலகுகள்
= 2 × 22 / 7 × 14
= 88 செ.மீ
எடுத்துக்காட்டு 2.3
ஒரு வட்டத்தின் சுற்றளவு 132 மீ எனில், அதன் ஆரம் மற்றும் விட்டம் காண்க. ( π =22/7 என்க)

தீர்வு

எடுத்துக்காட்டு 2.4
கடிகாரத்தில், 56 மி.மீ நீளமுள்ள வினாடி முள்ளின் முனை ஒரு நிமிடத்தில் கடக்கும் தொலைவைக் கணக்கிடுக. (இங்கு π =22/7)

தீர்வு
இங்கு, வினாடி முள்ளின் முனை ஒரு நிமிடத்தில் கடக்கும் தொலைவு என்பது வட்டத்தின் சுற்றளவையும், வினாடி முள்ளின் நீளம் என்பது அவ்வட்டத்தின் ஆரத்தையும் குறிக்கிறது. மேலும் ஆரம் r = 56 மி.மீ.
வட்டத்தின் சுற்றளவு C = 2πr அலகுகள்
= 2× (22/7) ×56
= 2×22×8
= 352 மி.மீ
ஆகவே, வினாடி முள்ளின் முனை, 1 நிமிடத்தில் கடக்கும் தொலைவு 352 மி.மீ.
எடுத்துக்காட்டு 2.5
ஒரு டிராக்டர் வண்டிச் சக்கரத்தின் ஆரம் 77 செ.மீ எனில், அது 35 முறை சுற்றும்போது, கடக்கும் தொலைவைக் காண்க. (π =22/7 என்க)
தீர்வு

ஒரு சுழற்சியில் கடக்கும் தொலைவு = வட்டத்தின் சுற்றளவு
= 2πr அலகுகள்
= 2 × 22/7 × 77
= 2 × 22× 11
= 484 செ.மீ
எனவே, ஒரு சுற்றில் கடக்கும் தொலைவு = 484 செ.மீ
35 சுற்றில் கடக்கும் தொலைவு = 484 × 35 = 16940 செ.மீ
எடுத்துக்காட்டு 2.6
ஒரு விவசாயி, 420 மீ ஆரமுடைய வட்ட வடிவில் அமைந்திருக்கும் கோழிப் பண்ணையைச் சுற்றி, முள்வேலி அமைக்க விரும்புகிறார். அதற்கு ஒரு மீட்டருக்கு ₹ 12 வீதம் செலவாகும். அவரிடம் ₹ 30,000 உள்ளது எனில், அவரது பண்ணைக்கு முள்வேலி அமைக்க இன்னும் எவ்வளவு பணம் தேவைப்படும்? (இங்கு, π= 22/7 )
தீர்வு
கோழிப்பண்ணையின் ஆரம் = 420 மீ
தேவையான முள்வேலியின் நீளம் என்பது வட்டத்தின் சுற்றளவு ஆகும்.
வட்டத்தின் சுற்றளவு C = 2πr அலகுகள்
= 2 × 22/7 × 420
= 2 × 22 × 60
ஆகவே, தேவையான முள்வேலியின் நீளம் = 2640 மீ
மீட்டருக்கு ₹ 12 வீதம் பண்ணைக்கு முள்வேலி அமைக்க ஆகும் செலவு = 2640 × 12
= ₹ 31,680
அவனிடம் உள்ள தொகை ₹ 30,000 எனக் கொடுக்கப்பட்டுள்ளது.
ஆகவே, தேவையான தொகை = ₹ 31,680 - ₹ 30,000 = ₹ 1,680.
எடுத்துக்காட்டு 2.7
படம் 2.9 இல் உள்ள உருவத்தின் சுற்றளவு காண்க. (இங்கு, π = 22/7)
தீர்வு

இந்த உருவத்தில், செவ்வகத்தின் ஒவ்வொரு பக்கங்கள் மீதும் அமைந்த அரைவட்டங்களின் சுற்றளவைக் கணக்கிட வேண்டும். இவ்வுருவம், இரு வெவ்வேறு அளவுள்ள அரை வட்டங்களால் உருவாக்கப்பட்டுள்ளது. அந்த அரைவட்டங்களின் விட்டங்கள் 7 செ.மீ மற்றும் 14 செ.மீ.
வட்டத்தின் சுற்றளவு C = πd அலகுகள் என்று அறிவோம்.
எனவே, அரைவட்டத்தின் சுற்றளவு =1/2 πd அலகுகள்
7 செ.மீ விட்டமுள்ள அரைவட்டத்தின் சுற்றளவு = 1/2 × 22/7 × 7=11 செ.மீ
ஒரு சோடி (II மற்றும் IV) அரை வட்டங்களின் சுற்றளவு = 2×11 = 22 செ.மீ
இதேபோல், 14 செ.மீ விட்டமுள்ள அரை வட்டத்தின் சுற்றளவு =1/2 × 22/7 × 14 = 22 செ.மீ
ஒரு சோடி (I மற்றும் III ) அரை வட்டங்களின் சுற்றளவு = 2 × 22 = 44 செ.மீ
எனவே, கொடுக்கப்பட்ட உருவத்தின் சுற்றளவு = 22 + 44 = 66 செ.மீ
எடுத்துக்காட்டு 2.8
கண்ணன் என்பவர் 14 செ.மீ ஆரமுள்ள ஒரு வட்டத் தகட்டை நான்கு சமபாகங்களாகப் பிரிக்கிறார். அதன் ஒரு கால் வட்டத் தகட்டின் சுற்றளவு காண்க. (இங்கு, π = 22/7)
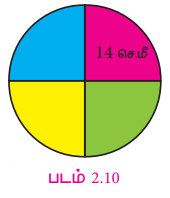
தீர்வு
கால் வட்டத் தகட்டின் சுற்றளவு காண, முதலில் அந்தக் கால்வட்டத்தின் வில்லின் சுற்றளவு காண வேண்டும்.
வட்டத்தின் ஆரம் (r) = 14 செ.மீ
வட்டத்தின் சுற்றளவு = 2πr அலகுகள்
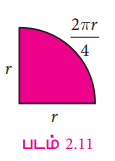
எனவே, கால்வட்டத்தின் வில்லின் சுற்றளவு =1/4 × 2πr
= πr/2
= 22/7 × 14/2
= 22 செ.மீ
கொடுக்கப்பட்ட வட்டத்தின் ஆரம் = 14 செ.மீ
ஆகவே, தேவையான உருவத்தின் சுற்றளவு, C =14+14+22
= 50 செ.மீ
சிந்திக்க
(i) ஓர் அரைவட்ட வில்லின் சுற்றளவும், அதே ஆரமுள்ள அரைவட்டத் தகட்டின் சுற்றளவும் சமமாகுமா? விவாதிக்க.
(ii) போக்குவரத்துக் கட்டுப்பாட்டு விளக்குகள் (traffic lights) வட்ட வடிவத்திலேயே இருக்கும். ஏன்?
(iii) தண்ணீர் தேங்கி நிற்கும் ஒரு குட்டையில், ஒரு கல்லை எறிந்தால், அதன் அதிர்வு அலைகள் வட்டமாகவே இருக்கும். ஏன்?