வட்டத்தின் பரப்பளவு (Area of the Circle)

வட்டத்தின் பரப்பளவு (Area of the Circle)

பின்வரும் சூழலைக் கருதுக.

ஒரு கம்பத்தில், ஒரு காளைமாடு கயிற்றால் கட்டப்பட்டுள்ளது. அந்த மாடு சுற்றி வந்து புல்லை மேய்கிறது எனில், அந்த மாடு மேயக்கூடிய அதிகபட்சப் பகுதி என்னவாக இருக்கும்?

இந்தச் சூழலில் நாம் கண்டறிய வேண்டியது பரப்பளவா அல்லது சுற்றளவா? ஆம். நாம் கண்டறிய வேண்டியது, வட்டப்பகுதியின் பரப்பளவு ஆகும்.

நாம் ஏற்கனவே கற்றறிந்த செவ்வகத்தின் பரப்பளவைக் காணும் முறையைப் பயன்படுத்தி, வட்டத்தின் பரப்பளவைக் காணலாம்.

1. தாளில் ஒரு வட்டம் வரைக.

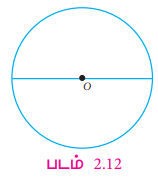
2. அதன் விட்டம் வழியே, அதனை இரண்டாக மடித்து, இரு அரைவட்டங்களாக்குக. அந்த வட்டத்தின் ஒரு பாதியை நிழலிடுக. (படம் 2.13)

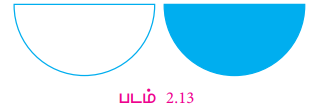
3. அந்த அரை வட்டத்தை மீண்டும் மடித்து, நான்கு கால்பகுதிகளாக்குக. (படம் 2.14) இல் வட்டமானது நான்கு கால் பகுதிகளாகப் பிரிக்கப்பட்டதைக் காட்டுகிறது. படம் 2.15 இல் உள்ள உருவம்போல, அந்த நான்கு கால்பகுதிகளையும் மாற்றி அமைக்கலாம்.

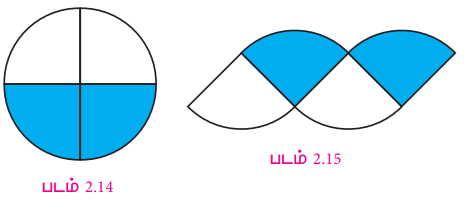
4. இச்செயலை மீண்டும் செய்வதன்மூலம் நான்கு பகுதிகள், எட்டுப் பகுதிகளாகப் படம் 2.16 இல் உள்ளவாறு சிறுபாகங்களாகும். படம் 2.17இல் உள்ளபடி, அச்சிறு பகுதிகளை மாற்றியமைத்துப் புதிய உருவத்தை அமைக்கலாம்.

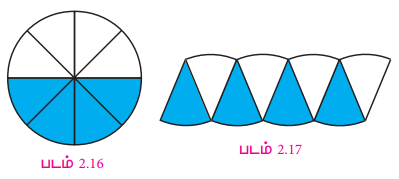
5. இவ்வாறு தொடர்ந்து செய்வதன்மூலம், அந்த வட்டம், 16 சமபாகங்களாகப் பிறகு 32 சம பாகங்களாக, உள்ளபடி பிரியும். சம பாகங்களின் எண்ணிக்கை அதிகரிக்க, அதிகரிக்க அதனை மாற்றி அமைப்பதால் உருவாகும் உருவம் படம் 2.19 இல் உள்ளது போல, ஏறத்தாழ, ஒரு செவ்வகமாகும்.

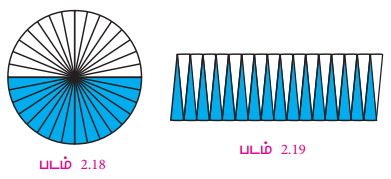
6. அந்தச் செவ்வகத்தின் மேல் மற்றும் அடிப்பக்கம், ஏறக்குறைய அந்த வட்டத்தின் சுற்றளவுக்குச் சமமாகும். எனவே, அதன் மேற்பக்க நீளம், வட்டத்தின் சுற்றளவில் பாதி ஆகும். அதாவது, πr ஆகும். அச்செவ்வகத்தின் உயரம் என்பது வட்டத்தின் ஆரத்திற்கு ஏறத்தாழச் சமமாகும். 

ஆகவே, சம பாகங்களின் எண்ணிக்கை மிக அதிகமாக இருக்கும்போது, அந்த வட்டத்தை நீளம் 'r' மற்றும் அகலம் ‘r’ உள்ள செவ்வகமாக மாற்றியமைக்க முடியும். இப்போது,

செவ்வகத்தின் பரப்பளவு =l × b ச. அலகுகள் 

= πr × r 

= πr2

= வட்டத்தின் பரப்பளவு

ஆகவே, வட்டத்தின் பரப்பளவு A = πr2 ச. அலகுகள்.

செயல்பாடு

ஒரு வரைபடத்தாளில், பல்வேறு அளவுகளில் வட்டங்கள் வரைக. அந்த வட்டங்களின் பரப்பளவை, அவ்வட்டம் உள்ளடக்கிய சதுரங்களை எண்ணுதல் மூலம் காண்க. சில சதுரங்கள் முழுமையாக வட்டத்திற்குள் அமையாது. எனவே, நாம் வட்டத்தின் பரப்பளவைத் தோராயமாகவே கண்டறிகிறோம்.

ஸ்பைரோகிராப் (spirograph) மூலம் பெறப்படும் வடிவங்கள் 

கீழே கொடுக்கப்பட்ட சில வடிவங்கள் ஸ்பைரோகிராப் (spirograph) பயன்படுத்தி உருவாக்கப்பட்டவை. இவ்வடிவங்களை உற்று நோக்கினால், ஒவ்வொன்றும் வெவ்வேறு வடிவமைப்பிலான வட்டங்களாக இருப்பதைக் காணலாம்.

சிந்திக்க

ஒரு வட்டத்தின் சுற்றளவும், பரப்பளவும் எண்ணளவில் சமம் எனில், அதன் ஆரத்தின் மதிப்பைக்  காண இயலுமா?

எடுத்துக்காட்டு 2.9  

ஆரம் 21 செ.மீ அளவுள்ள வட்டத்தின் பரப்பளவு காண்க. (π=3.14 என்க)

தீர்வு

ஆரம் (r) = 21 செ.மீ

வட்டத்தின் பரப்பளவு = πr2 ச. அலகுகள் 

= 3.14 × 21 × 21 

= 1384.74

= 1384.74 செ.மீ2   

எடுத்துக்காட்டு 2.10    

28 செ.மீ விட்டமுள்ள சாகச வளையத்தின் (hula loop) பரப்பளவைக் காண்க (π = 22 /7 என்க)

தீர்வு

கொடுக்கப்பட்ட விட்டம் (d) = 28 செ.மீ

ஆரம் (r) = 28/2 = 14 செ.மீ 

வட்டத்தின் பரப்பளவு = πr2 ச. அலகுகள்

= 22/7 × 14 × 14

ஆகவே, வட்டத்தின் பரப்பளவு = 616 செ.மீ2

எடுத்துக்காட்டு 2.11 

ஒரு வட்டத்தின் பரப்பளவு 2464 செ.மீ2. அதன் ஆரம் மற்றும் விட்டம் காண்க.

(π=22/7 என்க)

தீர்வு

வட்டத்தின் பரப்பளவு = 2464 செ.மீ2

πr2 = 2464

 22/7 × r2 = 2464

r2 = 2464 × 7/22

r2 = 112 × 7 = 784

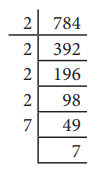
r2 =2×2×2×2×7×7

= 4×4×7×7

 = 42 ×72

 r2 = (4×7)2       [r×r = (4×7)×(4×7)]

 r = 4×7

 = 28 செ.மீ

 விட்டம்  (d) = 2 × r = 2 × 28 = 56 செ.மீ.

எடுத்துக்காட்டு 2.12

154 மீ சுற்றளவு உள்ள ஒரு வட்ட வடிவப் பூங்காவைச் சுற்றி ஒரு தோட்டக்காரர் நடக்கிறார். அதனைச் செப்பனிடச் சதுர மீட்டருக்கு ₹ 25 வீதம் ஆகும் மொத்த செலவு யாது? ( π = 22/7 என்க)

தீர்வு

அவர் நடந்த தொலைவு என்பது, அந்த வட்டத்தின் சுற்றளவுக்குச் சமமாகும். நடந்த தொலைவு 154 மீ எனக் கொடுக்கப்பட்டுள்ளது. எனவே,

வட்டத்தின் சுற்றளவு = 154 மீ

அதாவது, 2πr = 154

 2 × 22/7 × r = 154

 r =154 × (7/44)

 r = 3.5 × 7

 = 24.5

வட்ட வடிவப் பூங்காவின் பரப்பளவு = πr2 சதுர அலகுகள்

= (22/7) × 24.5 × 24.5

= 22 × 3.5 × 24.5

 = 1886.5 மீ2

ஒரு சதுர மீட்டர் பரப்பளவு பூங்காவைச் சமன்படுத்த ஆகும் செலவு = ₹ 25. 

எனவே, 1886.5 ச. மீ பூங்காவைச் சமன்படுத்த ஆகும் செலவு

= 1886.5 × 25 = ₹ 47,162.50

எடுத்துக்காட்டு 2.13  

கயிற்றால் கட்டப்பட்ட மாடு மேய்ந்த பகுதியின் பரப்பளவு 9856 ச.மீ எனில், கயிற்றின் நீளம் காண்க. ( π = 22/7)

தீர்வு

கொடுக்கப்பட்ட வட்டத்தின் பரப்பளவு = 9856 ச.மீ

 πr2 = 9856

 (22/7)  × r2 = 9856

 r2 = 9856 × 7/22

 r2  = 448 × 7 = 3136

 r2 = 2 × 2 × 2 × 2 × 2 × 2 × 7 × 7

 r2 = 8 × 8 × 7 × 7 = 82 × 72 = (8 × 7)2

 r = 8 × 7 = 56 மீ

ஆகவே, தேவையான கயிற்றின் நீளம் 56 மீ.

எடுத்துக்காட்டு 2.14 

ஒரு செவ்வகத்தின் இருபுறமும் அரைவட்டம் இணைந்த வடிவில் (படம் 2.21) ஒரு தோட்டம் அமைந்துள்ளது. அந்தச் செவ்வகத்தின் நீளம் மற்றும் அகலம் முறையே 16 மீ மற்றும் 8 மீ எனில், பின்வருவனவற்றைக் கணக்கிடுக.

(i) தோட்டத்தின் சுற்றளவு

(ii) தோட்டத்தின் மொத்தப் பரப்பளவு 

தீர்வு

(i) தோட்டத்தின் சுற்றளவு என்பது, செவ்வகத்தின் இரு நீளங்கள் 16 மீ மற்றும் இரு 8 மீ விட்டமுள்ள அரைவட்டங்களின் சுற்றளவு இணைந்தது.

அரைவட்டத்தின் சுற்றளவு = πd/2 அலகுகள்

= π ×8 / 2 = 4 π

= 4 × 3.14

= 12.56 மீ

ஆகவே, இரு அரைவட்டங்களின் சுற்றளவு = 2 × 12.56

= 25.12 மீ

தோட்டத்தின் சுற்றளவு = நீளம்+நீளம்+இரு அரை வட்டங்களின் சுற்றளவு

= 16 +16 + 25.12

= 32 + 25.12

= 57.12 மீ

(ii) தோட்டத்தின் மொத்தப் பரப்பளவு

= செவ்வகத்தின் பரப்பளவு + இரு அரை வட்டங்களின் பரப்பளவு

= செவ்வகத்தின் பரப்பளவு + வட்டத்தின் பரப்பளவு 

இங்குச் செவ்வகத்தின் பரப்பளவு = l × b ச. அலகுகள்

= 16×8

= 128 மீ2 ……(1)

வட்டத்தின் பரப்பளவு = πr2 ச. அலகுகள்

= 3.14 × 4 × 4

= 3.14 × 16

= 50.24 மீ2 ……(2)

(1) ,(2) லிருந்து தோட்டத்தின் மொத்தப் பரப்பளவு = 128 + 50.24

=178.24 மீ2

இவற்றை முயல்க

ஒரு வரைபடத் தாளில், வெவ்வேறு ஆரங்களுடைய வட்டங்கள் வரைக. அந்த வட்டத்திற்குள் அடைபடும் சதுரங்களை எண்ணி, அவ்வட்டத்தின் பரப்பளவைக் காண்க. மேலும் சூத்திரப்படி பரப்பளவைக் கணக்கிடுக.

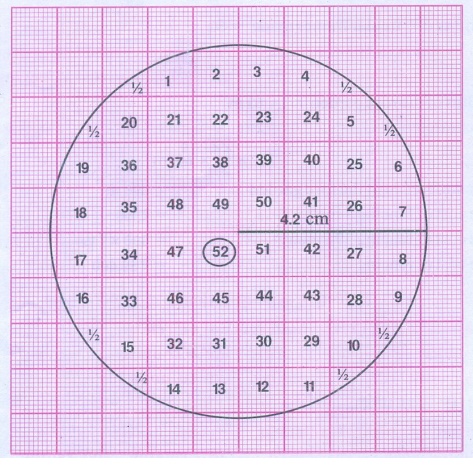
வட்டத்திற்குள் அடைபடும் சதுரங்களின் எண்ணிக்கை  = 52 + 8 × ½

 = 52 + 4 = 56

வட்டத்தின் ஆரம் r = 4.2 செ.மீ

வட்டத்தின் பரப்பளவு  = πr2

= 22/7 × 4.2 ⊂ 4.2 சதுர செ.மீ

= 55.44 சதுர செ.மீ

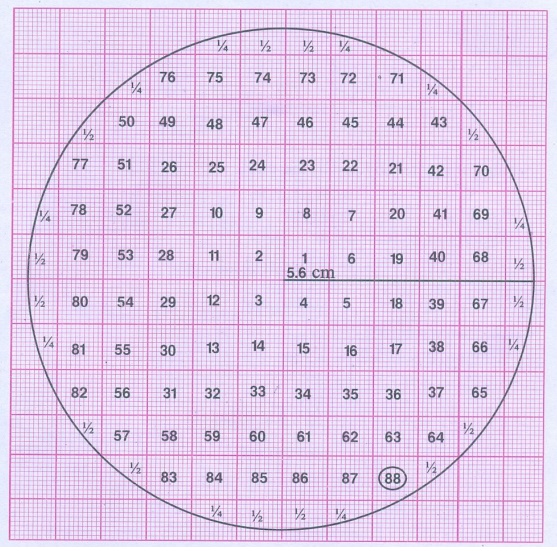
வட்டத்திற்குள் அடைபடும் சதுரங்களின் எண்ணிக்கை = 88 +16 × ½ +10 × ¼

 = 88 + 8 + 2 ½ = 98.5

வட்டத்தின் ஆரம் r = 5.6 செ.மீ

வட்டத்தின் பரப்பளவு  = πr2

= 22/7 × 5.6 ⊂ 4.2 சதுர செ.மீ

= 98.56 சதுர செ.மீ

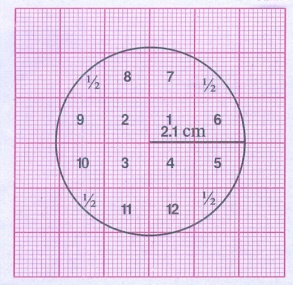
வட்டத்திற்குள் அடைபடும் சதுரங்களின் எண்ணிக்கை =12 + 4 × ½

 = 12 + 2 = 14

 வட்டத்தின் ஆரம் r = 2.1செ.மீ

வட்டத்தின் பரப்பளவு  = πr2

= 22/7 × 2.1 ⊂ 21 சதுர செ.மீ

= 13.86 சதுர செ.மீ

(i) 4.2 செ.மீ ஆரமுள்ள வட்டத்தின் பரப்பளவு காண்க. 

வட்டத்தின் ஆரம் r = 4.2 செ.மீ

வட்டத்தின் பரப்பளவு  = πr2

= 22/7 × 4.2 ⊂ 42 சதுர செ.மீ

= 55.44 சதுர செ.மீ

(ii) 28 செ.மீ விட்டமுள்ள வட்டத்தின் பரப்பளவு காண்க.

ஆரம் r = 14 cm

வட்டத்தின் பரப்பளவு = πr2

= 22/7 × 14 ⊂=14 சதுர செ.மீ

= 616 சதுர செ.மீ