உடன் தொடர்பின் வகைகள் - உடன்தொடர்புப் பகுப்பாய்வு | 12th Economics : Chapter 12 : Introduction to Statistical Methods and Econometrics
12ஆம் வகுப்பு பொருளாதாரம் : அத்தியாயம் 12 : புள்ளியியல் முறைகள் மற்றும் பொருளாதார அளவையியல் ஓர் அறிமுகம்
உடன்தொடர்புப் பகுப்பாய்வு
உடன்தொடர்புப் பகுப்பாய்வு (Y)
உடன்தொடர்புப் பகுப்பாய்வு என்பது இரண்டு அல்லது அதற்கு மேற்பட்ட மாறிகள் எவ்வாறு ஒன்றுடன் ஒன்று தொடர்பு கொண்டு மாறுகின்றன என்பதை பற்றி கணக்கிடுவது ஆகும். சர் ஃபிரான்சிஸ் கால்டன் என்பவர் இப்பகுப்பாய்வினைக் கண்டறிந்தார்.
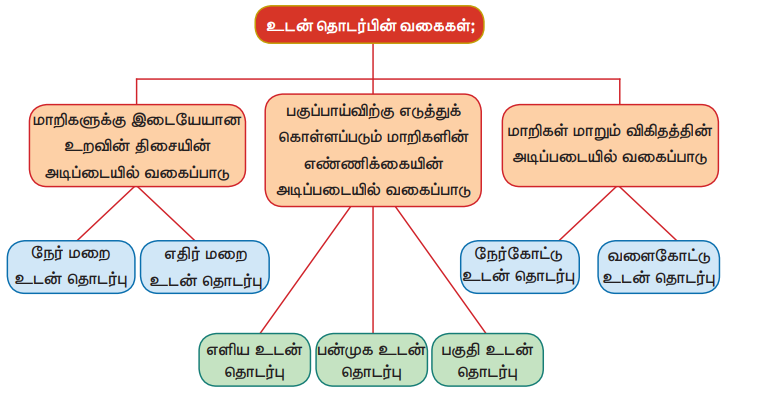
1. உடன் தொடர்பின் வகைகள்

உடன் தொடர்பை பலவாறு வகைப்படுத்தலாம் மாறிகளுக்கு இடையேயான உறவின் திசை, பகுப்பாய்வுக்கு எடுத்துக்கொள்ளும் மாறிகளின் எண்ணிக்கை, மற்றும் மாறிகளுக்கிடையேயான உறவின் தன்மை என்ற அடிப்படையில் நாம் அவைகளை வகைப்படுத்தலாம்.
I. மாறிகளுக்கு இடையேயான உறவின் திசை அடிப்படையில்
மாறிகள் ஒன்றுக்கொன்று நேர்மறையாகவோ அல்லது எதிர்மறையாகவோ உறவு கொண்டிருக்கும். அதன் அடிப்படையில் உடன் தொடர்பினை நேர்மறை உடன்தொடர்பு மற்றும் எதிர்மறை உடன்தொடர்பு என பாகுபடுத்தப்படுகின்றது.
நேர்மறை உடன்தொடர்பு
இரு மாறிகளின் மதிப்புகளும் ஒரே திசையில் நகர்ந்து சென்றால் அதனை நேர்முறை உடன்தொடர்பு என்கிறோம்.
உதாரணம் : வருமானம் அதிகரிக்கும் பொழுது செலவும் அதிகரிக்கிறது. ஆகவே வருமானம் மற்றும் செலவு மாறிகள் நேர்மறை உடன் தொடர்பைக் கொண்டிருக்கிறது என்கிறோம். உதாரணம் Y = a + bx
எதிர்மறை உடன்தொடர்பு
இரு மாறிகளின் மதிப்புகள் எதிர் எதிர் திசையில் நகர்ந்து சென்றால் அதனை எதிர்மறை உடன்தொடர்பு என்கிறோம்.
உதாரணம் : விலை அதிகரிக்கும்பொழுது பொருளுக்கான தேவை குறைந்து செல்கிறது. உதாரணம் Y = a – bx
II. பகுப்பாய்வுக்கு எடுத்துக்கொள்ளும் மாறிகளின் எண்ணிக்கையின் அடிப்படையில்:
உடன்தொடர்பு பகுப்பாய்வுக்கு எவ்வளவு எண்ணிக்கையிலான மாறிகளை எடுத்துக்கொள்கிறோம், அவற்றை எவ்வாறு பகுப்பாய்வுக்கு பயன்படுத்துகிறோம் என்ற வகையில் உடன் தொடர்பினை வகைப்படுத்தலாம். அவ்வகைகள்:
அ) எளிய உடன்தொடர்பு,
ஆ) பன்முக உடன்தொடர்பு
இ) பகுதி உடன்தொடர்பு
எளிய உடன்தொடர்பு
உடன்தொடர்பு பகுப்பாய்வில் ஒரு நேரத்தில் இரு மாறிகளை மட்டும் எடுத்துக்கொண்டால் அதனை எளிய உடன்தொடர்பு என்கிறோம். உதாரணம் Y = a + bx
பன்முக உடன்தொடர்பு
உடன் தொடர்பு பகுப்பாய்வில் இரண்டிற்கும் மேற்பட்ட காரணிகளை ஒருசேர எடுத்துக்கொண்டால் அது பன்முக உடன் தொடர்பு என்கிறோம். உதாரணத்திற்கு, தேவைக்கும், தேவையினை தீர்மானிக்கும் மாறிகளான குறிப்பிட்ட பொருளின் விலை, நுகர்வோரின் வருமானம், தொடர்புடைய பொருளின் விலை ஆகியவற்றை எடுத்து பகுப்பாய்வு செய்தால் அது பன்முக உடன்தொடர்பு ஆகும்.
உதாரணம்: Qd.= f (P, Pc, Ps, t, y) இதில் Qd பொருளின் தேவை
f - சார்பு
P - பொருளின் விலை
Pc - போட்டிப் பொருளின் விலை
Px - பதிலீட்டுப்பொருளின் விலை
t - நுகர்வோரின் விருப்பு வெறுப்புக்கள்
y - வருமானம்
பகுதி உடன்தொடர்பு
உடன்தொடர்பு பகுப்பாய்வில் இரண்டிற்கும் மேற்பட்ட காரணிகளை எடுத்துக்கொண்டாலும், அவற்றினில் இரண்டு காரணிகளை மட்டும் (மற்றவை மாறாமல் இருக்கும் என வைத்துக்கொண்டு) பகுத்தாய்ந்தால், அதனை பகுதி உடன் தொடர்பு என்கிறோம்.
III. பகுப்பாய்வுக்கு எடுத்துக்கொள்ளும் மாறிகளின் மாறும் விகித அடிப்படையில்
நாம் பகுப்பாய்வுக்கு எடுத்துக்கொண்ட மாறிகள் மாறும் விகிதம் ஒரே அளவில் இருக்கின்றதா, அல்லது மாறிக்கொண்டே இருக்கின்றதா என்பதன் அடிப்படையில் உடன்தொடர்பினை நேர்கோட்டு உடன்தொடர்பு, மற்றும் வளைகோட்டு உடன் தொடர்பு என வகைப்படுத்துகிறோம்.
நேர்கோட்டு உடன்தொடர்பு
இரு மாறிகளின் மாறும் விகிதங்கள் ஒரே அளவாக இருந்தால் அதனை நேர்கோட்டு உடன்தொடர்பு என்கிறோம். வரைபடைத்தில் அம்மாறிகளின் மதிப்புகளை குறித்து பார்த்தோமானால் அவை ஒரு நேர்கோட்டினை தரும். உதாரணம் Y = a + bx
வளைகோட்டு உடன்தொடர்பு
இரு மாறிகளின் மாறும் விகிதங்கள் ஒரே அளவாக இல்லாமல் குறைந்து வந்தாலோ, அல்லது அதிகரித்து வந்தாலோ அதனை வளைகோட்டு உடன் தொடர்பு என்கிறோம். மாறிகளின் மதிப்புக்களை வரைபடத்தில் குறித்து பார்த்தால் அவைகள் ஒரு வளைகோட்டினைத் தரும். உதாரணம் Y = a + bx2
உடன்தொடர்பினை அளவிடும் முறைகள்
உடன் தொடர்பினை அளவிடுதற்கு பல முறைகள் உள்ளன. அவைகள்:
1. சிதறல் விளக்கப்படம்
2. வரைபட முறை
3. கார்ல் பியர்சனின் உடன்தொடர்புக் கெழு முறை
4. மீச்சிறு வர்க்க முறை.
இம்முறைகளில் முதல் இரண்டும் வரைபட முறைகளாகும். அவை உடன்தொடர்பின் அளவினை பற்றி நமக்கு தோரயமான மதிப்பீட்டினை வழங்கும். பின்னர் சொல்லப்பட்ட இரண்டு முறைகளும், கணக்கீட்டின் அடிப்படையில் உடன்தொடர்பின் அளவினை நமக்கு துல்லியமாக வழங்கும்.
1. சிதறல் விளக்கப்பட முறை
கொடுக்கப்பட்ட மாறிகளின் (X,Y) மதிப்புக்களை வரைபடத்தில் குறித்து, அம்மதிப்புகள் எவ்வாறு சிதறியிருக்கின்றன, அவைகளின் தொடர்பின் போக்கு எவ்வாறு உள்ளது என ஆய்வதன் மூலம் நாம் உடன்தொடர்பினை கண்டறியலாம்.
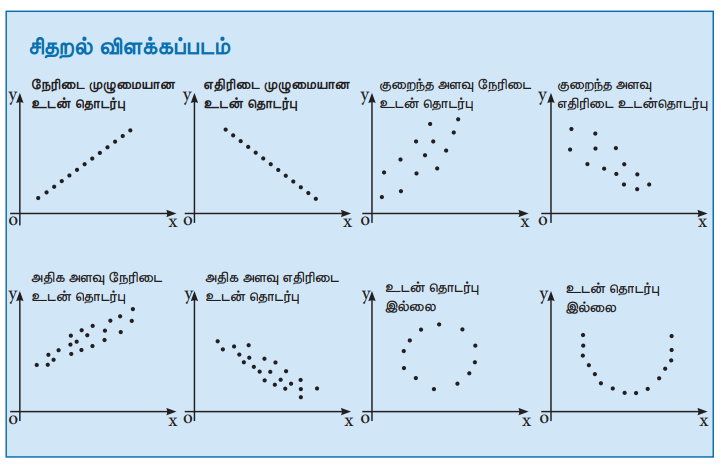
சிதறல் விளக்கப்பட முறையின் நன்மைகள்
(1) இது மிகவும் எளிமையான மற்றும் கணக்கீடுகளற்ற முறையாகும்.
(2) இது கடைநிலை மதிப்புக்களினால் பாதிக்கப்படுவதில்லை
(3)மாறிகளுக்கிடையேயான உடன்தொடர்பைக் கண்டறிவதில் இது ஒரு அடிப்படை நிலை.
சிதறல் விளக்கப்பட முறையின் குறைபாடுகள்
சிதறல் விளக்கப்பட முறையினை கொண்டு மாறிகளுக்கிடையேயான உடன் தொடர்பினை (ஒருசில சூழ்நிலைகளைத் தவிர) துல்லியமாக கணக்கிட முடியாது. அவைகளுக்கிடையேயான உறவு அதிகமாக இருக்கிறதா அல்லது குறைவாக இருக்கிறதா என்பதனை மட்டுமே நாம் கூற இயலும்.
2. வரைபட முறை
இம்முறையில் ஒரே வரைபடத்தில் நாம் உடன் தொடர்பை பகுப்பாய்வுக்கு எடுத்துக்கொண்ட மாறிகளின் மதிப்பினைக் குறித்து அந்தந்த மாறிகளின் மதிப்புகளை கோட்டினால் இணைக்க வேண்டும். இப்பொழுது இரு மாறிமதிப்புகளுக்கும் இரு தனித்தனியான கோடு கிடைக்கும். இப்பொழுது அக்கோடுகள் செல்லும் திசை, கோடுகளுக்கிடையேயான இணைந்த போக்கு ஆகியவற்றின் அடிப்படையில் நாம் உடன்தொடர்பினை தோராயமாகக் கூறலாம். கோடுகள் ஒரே திசையில் நகர்ந்தால் அவைகளுக்கு இடையே நேர்மறை உடன்தொடர்பு எனவும், எதிர் எதிர் திசையில் இருந்தால் எதிர்மறை உடன்தொடர்பு எனவும் காணலாம். கோடுகள் கிட்டத்தட்ட இணைகோடுகளாகஇருந்தால் அவைகளுக்கிடையேயான உடன் தொடர்பு அளவு அதிகம் எனலாம்.
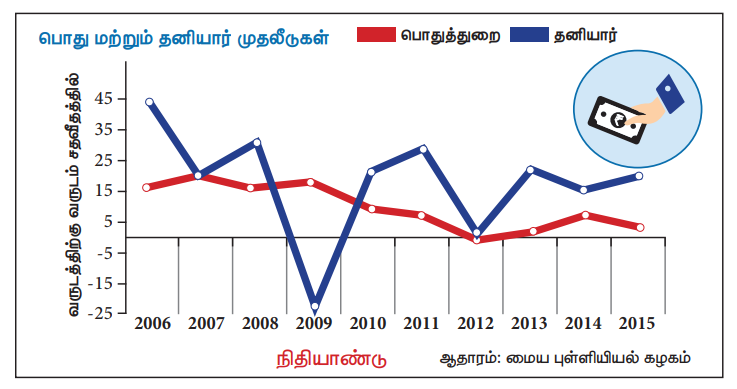
3. கார்ல் பியர்ஸனின் உடன்தொடர்புக் கெழு முறை
கார்ல் பியர்ஸனின் உடன்தொடர்புக் கெழு '' என குறிப்பிடப்படுகிறது. இக்கெழு இரண்டு மாறிகளுக்கு இடையேயான உறவின் அளவினையும், உறவின் திசையையும் குறிப்பிடுகிறது. இதைக் கணக்கிடுவதற்கான சூத்திரங்கள்:
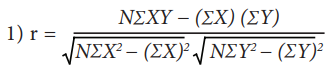
இம்முறையில் சராசரியிலிருந்தோ ஊக சராசரியிலிருந்தோ விலக்கங்களை கண்டுபிடிப்பதில்லை .
2) உண்மையான சராசரியிலிருந்து விலகல் முறை
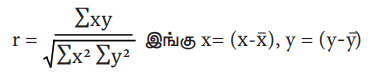
3) அனுமானிக்கப்பட்ட சராசரியிலிருந்து விலகல் முறை
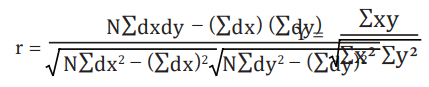
இங்கு ,
dx = (x-A) ஒவ்வொரு X ன் மதிப்பையும் அனுமானிக்கப்பட்ட சராசரியைக் கொண்டு கழிப்பது.
dy (y-B) ஒவ்வொரு y ன் மதிப்பையும் அனுமானிக்கப்பட்ட சராசரியைக் கொண்டு கழிப்பது.
∑dxdy = dx மற்றும் dy இரண்டையும் பெருக்கி வரும் கூட்டுத்தொகை.
∑dx2= ஒவ்வொரு dx -க்கான வர்க்கத்தின் கூட்டுத்தொகை
∑dy2 = ஒவ்வொரு dy -க்கான வர்க்கத்தின் கூட்டுத்தொகை
∑dx = (X - A) மதிப்பின் கூட்டுத்தொகை
∑dy = (Y - B) மதிப்பின் கூட்டுத் தொகை
சராசரியிலிருந்து விலக்க முறையில் கார்ல் பியர்ஸனின் உடன் தொடர்புக் கெழுவினை கண்டறியும் நிலைகள்
* படி-1 X மற்றும் Y மாறிகளின் கூட்டுச் சராசரிகளைக் கணக்கிடவும்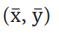
* படி-2 X மற்றும் Y மதிப்புக்கள் அதனதன் சராசரி மதிப்பிலிருந்து உள்ள விலக்கத்தைக் கணக்கிடவும் 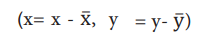
* படி-3 x விலக்கங்களின் வர்க்கத்தைக் (x2) கணக்கிட்டு கூட்டவும் (∑x2). இதுபோல் y விலக்கங்களின் வர்க்கத்தைக் (y2) கணக்கிட்டு கூட்டவும் (∑y2)
* படி-4 ஒவ்வொரு X மதிப்பு விலக்கத்தையும் அதனுடைய y மதிப்பு விலக்கத்தையும் பெருக்கி (xy) அம்மதிப்புக்களைக் கூட்டவும் ∑xy.
* படி-5 இக்கூட்டல் மதிப்புக்களை என்ற 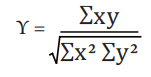 சூத்திரத்தில் பிரதியிட்டு Y மதிப்பு கணக்கிடவும்.
சூத்திரத்தில் பிரதியிட்டு Y மதிப்பு கணக்கிடவும்.
காரல் பியர்சன் ஒட்டுறவு கெழு வகைப்படுத்தப்படாத புள்ளி விவரம்
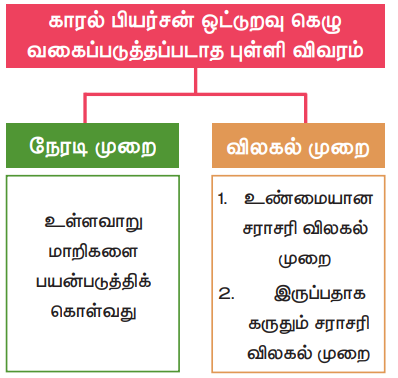
1. கூட்டுச்சராசரி விலக்கமுறை
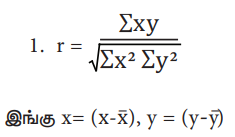
சுருக்குமுறை
2. உறுப்பு மதிப்புக்களை நேரடியாக பயன்படுத்தும் போது
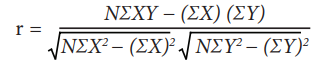
3. ஊகச் சராசரி விலக்க முறை
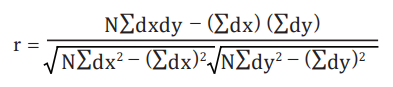
dx= (X-A) மற்றும் dy = (Y-B)
A, B ஊகச் சராசரிகள்
Y ஆதிப்புள்ளி மாற்றத்தால் பாதிக்கப்படுவதில்லை
Y அளவிடும் அலகு மாற்றத்தால் பாதிக்கப்படுவதில்லை
-1 ≤ r ≤ + 1
உடன் தொடர்பினைக் கணக்கிடும் முறை
நேரடி முறை
உதாரணம் 1 : பின்வரும் விவரங்களுக்கு ஒட்டுறவுக் கெழுவினை கண்டறிந்து அதனை விளக்கவும்.
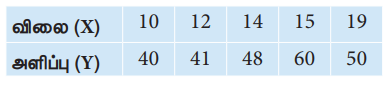
தீர்வு உறுப்பு மதிப்புக்களை நேரிடையாகப் பயன்படுத்தும் முறை
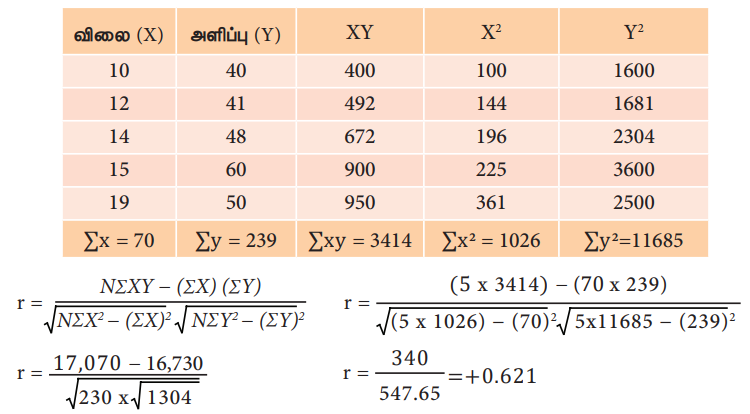
மேற்கண்ட உதாரணத்தில் உடன்தொடர்புக் கெழுவின் அளவு 0.0621 என்றிருக்கிறது. ஆகவே, பொருளின் விலைக்கும், அளிப்பிற்கும் நேரடி மற்றும் குறிப்பிடத்தகுந்த அளவுக்கு உறுதியான உறவும் உள்ளது.
உண்மைச் சராசரியின் அடிப்படையில் ஒட்டுறவினை கண்டறிதல்
உதாரணம் 1 : பின்வரும் விவரங்களுக்கு உண்மைச் சராசரியை பயன்படுத்தும் சூத்திரத்தினை பயன்படுத்தி கார்ல் பியர்ஸனின் ஒட்டுறவுக் கெழுவினை கண்டறிக
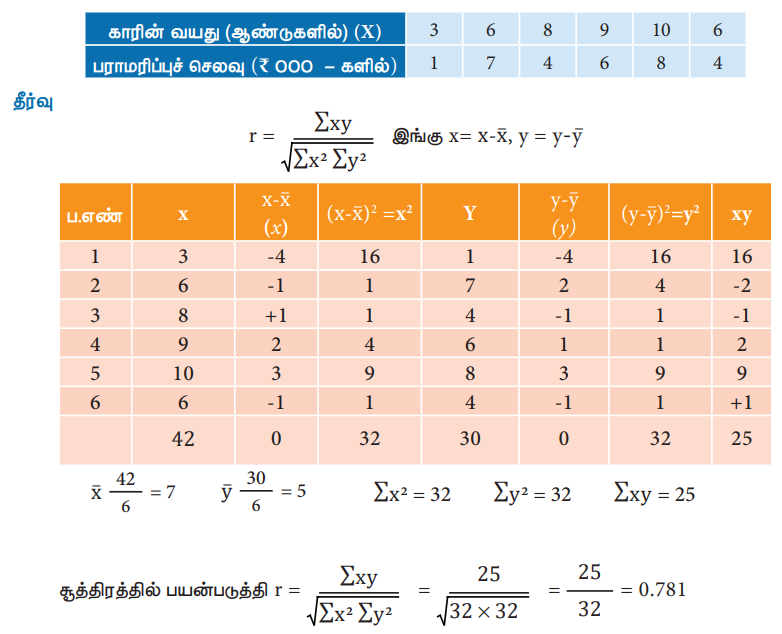
r = 0.781, உடன் தொடர்புக் கெழு மிக அதிகமாகவும் நேரிடையாகவும் உள்ளது. ஆகவே, காரின் வயதிற்கும், பராமரிப்புச் செலவிற்கும் நேரடித் தொடர்பு, மிக அதிக அளவில் உள்ளது.
ஊக சராசரியினை பயன்படுத்தும் சூத்திரத்தினை கொண்டு உடன்தொடர்பு கணக்கிடுதல்:
உதாரணம் 1; பின்வரும் விவரங்களுக்கு கார்ல் பியர்ஸனின் உடன்தொடர்புக் கெழுவினை கண்டறிக.
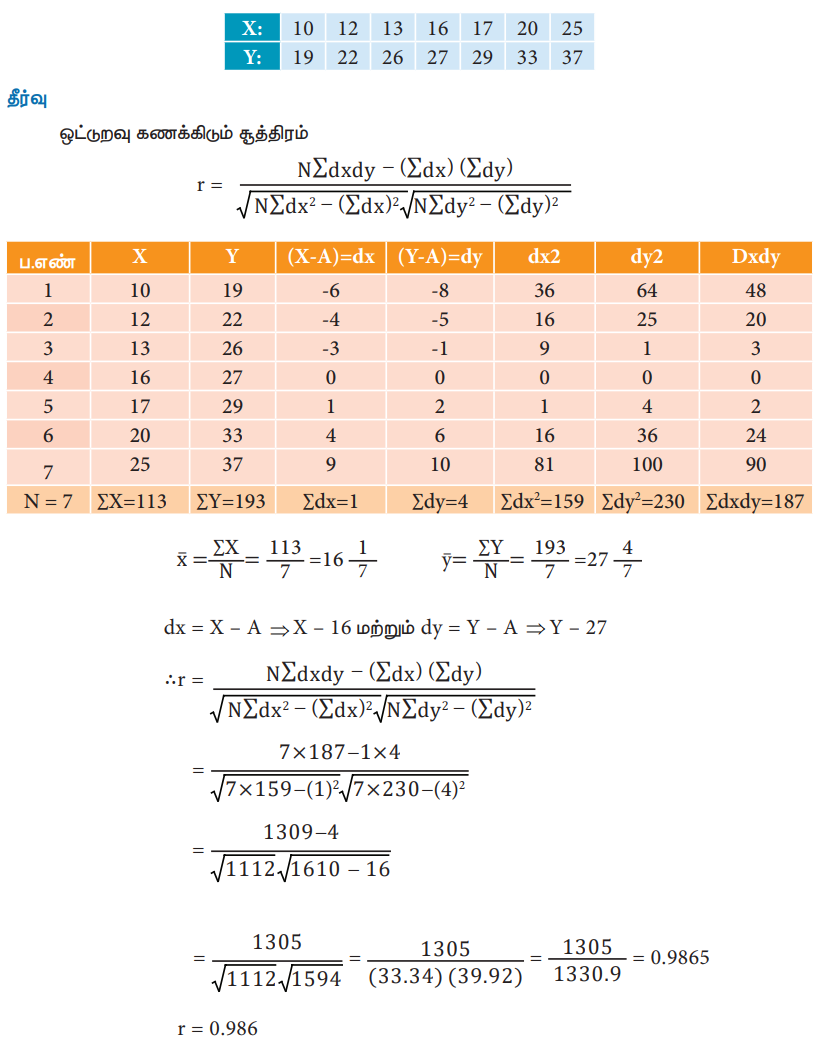 மேற்கண்ட உடன்தொடர்பு பகுப்பாய்வில் X மற்றும் Y காரணிகளுக்கிடையே நேரிடையான மிக அதிக உடன் தொடர்பு இருக்கின்றது.
மேற்கண்ட உடன்தொடர்பு பகுப்பாய்வில் X மற்றும் Y காரணிகளுக்கிடையே நேரிடையான மிக அதிக உடன் தொடர்பு இருக்கின்றது.