Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«»Я«▓Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«│Я»Ї Я«фЯ«цЯ«┐Я«▓Я»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»ЂЯ«ЋЯ«│Я»Ї | Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї | Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЁЯ«ЪЯ»ѕЯ«»Я«ЙЯ«│Я««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЂЯ«цЯ«▓Я»Ї (Decimal Representation to Identify Irrational Numbers) | 9th Maths : UNIT 2 : Real Numbers
9 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 2 : Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї
Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЁЯ«ЪЯ»ѕЯ«»Я«ЙЯ«│Я««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЂЯ«цЯ«▓Я»Ї (Decimal Representation to Identify Irrational Numbers)
6. Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЁЯ«ЪЯ»ѕЯ«»Я«ЙЯ«│Я««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЂЯ«цЯ«▓Я»Ї (Decimal Representation to Identify Irrational Numbers)
Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ«џЯ«« Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«хЯ»ѕ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ««Я«▓Я»ЂЯ««Я»Ї, Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕ Я«ЄЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»ЂЯ««Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ«цЯ»ѕ Я«еЯ«ЙЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї. Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, ¤ђ Я«ЄЯ«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЕЯ«цЯ»Ђ 3.14159265358979... Я«јЯ«ЕЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«┐, Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я«▒Я»ЇЯ«▒Я«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, ¤ђ Я«ЄЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«цЯ»Ї Я«цЯ»ЂЯ«▓Я»ЇЯ«▓Я«┐Я«»Я««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒ Я««Я»ЂЯ«ЪЯ«┐Я«»Я«ЙЯ«цЯ«цЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«ЋЯ«│Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї.
(i) 0.1011001110001111...
(ii) 3.012012120121212...
(iii) 12.230223300222333000...
(iv) Рѕџ2 = 1.4142135624...
Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«Й Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«Й? Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕ.... Я«ЁЯ«хЯ»ѕ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«хЯ»ЂЯ««Я«┐Я«▓Я»ЇЯ«▓Я»ѕ, Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕ Я«ЅЯ«ЪЯ»ѕЯ«»Я«ЕЯ«хЯ»ЂЯ««Я«┐Я«▓Я»ЇЯ«▓Я»ѕ . Я«јЯ«ЕЯ«хЯ»Є, Я«ЁЯ«хЯ»ѕ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓. Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ p/q, (p, q, Рѕѕ Рёц Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї qРЅа0) Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«ц Я«ЄЯ«»Я«▓Я«ЙЯ«цЯ»Ђ. Я«ЁЯ«хЯ»ѕ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.8
Рѕџ3 Я«ЄЯ«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ

Я«јЯ«ЕЯ«хЯ»Є, Я«еЯ»ђЯ«│Я»Ї Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐, Рѕџ3 = 1.7320508...
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я««Я»ЂЯ«┤Я»Ђ Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ««Я«▒Я»ЇЯ«▒ Я««Я«┐Я«ЋЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ««Я»ѓЯ«▓Я««Я»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ«▒Я«┐Я«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Рѕџ2, Рѕџ3, Рѕџ5, Рѕџ6, Рѕџ7, ... Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«хЯ«┐Я«цЯ«┐Я««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Є.
Рѕџ2 = 1.414, Рѕџ3 = 1.732, ¤ђ = 3.141, Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«ЁЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«ЪЯ«┐Я«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї. Я«ЁЯ«хЯ»ѕ Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Є, Я«цЯ»ЂЯ«▓Я»ЇЯ«▓Я«┐Я«»Я««Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ«▓Я»ЇЯ«▓. ¤ђ Я«ЄЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕ 22/7. 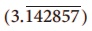 Я«јЯ«Е Я«еЯ«ЙЯ««Я»Ї Я«ЁЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«ЪЯ«┐ Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ«хЯ»ѕ Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЄЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЕЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я«▒Я»ЇЯ«▒Я«цЯ»Ђ. Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»ЂЯ«▓Я»ЇЯ«▓Я«┐Я«»Я««Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕ .
Я«јЯ«Е Я«еЯ«ЙЯ««Я»Ї Я«ЁЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«ЪЯ«┐ Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЁЯ«хЯ»ѕ Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЄЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЕЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я«▒Я»ЇЯ«▒Я«цЯ»Ђ. Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»ЂЯ«▓Я»ЇЯ«▓Я«┐Я«»Я««Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕ .
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.9
Я«ЋЯ»ђЯ«┤Я»ЂЯ«│Я»ЇЯ«│Я«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«хЯ«ЋЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«Ћ.
(i) Рѕџ10 (ii) Рѕџ49 (iii) 0.025 (iv) ![]() (v) 2.505500555... (vi) Рѕџ2/2
(v) 2.505500555... (vi) Рѕџ2/2
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
(i) Рѕџ10 Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї (Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї 10 Я«њЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»ЂЯ«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ Я«јЯ«БЯ»Ї Я«ЁЯ«▓Я»ЇЯ«▓).
(ii) Рѕџ49 = 7 = 7/1, Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї (49 Я«њЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»Ђ Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ Я«јЯ«БЯ»Ї).
(iii) 0.025 Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї (Я«ЄЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«јЯ«БЯ»Ї).
(iv) ![]() = 0.7666.... Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї (Я«ЄЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«џЯ«« Я«јЯ«БЯ»Ї).
= 0.7666.... Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї (Я«ЄЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«џЯ«« Я«јЯ«БЯ»Ї).
(v) 2.505500555.... Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї (Я«ЄЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я«▒Я»ЇЯ«▒ Я«цЯ«џЯ«« Я«јЯ«БЯ»Ї)
(vi) 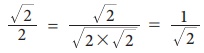 Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї (2 Я«њЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»Ђ Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ Я«јЯ«БЯ»Ї Я«ЁЯ«▓Я»ЇЯ«▓).
Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї (2 Я«њЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»Ђ Я«хЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ Я«јЯ«БЯ»Ї Я«ЁЯ«▓Я»ЇЯ«▓).
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.10
0.12 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 0.13 Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«јЯ«хЯ»ѕЯ«»Я»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
0.12, 0.13 Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ 3 Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї 0.12010010001.... , 0.12040040004...., 0.12070070007...
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ:
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.9, (vi) Я«ЄЯ«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ѕЯ«цЯ»Ї Я«цЯ«хЯ«▒Я»ЂЯ«цЯ«▓Я«ЙЯ«Ћ p/q Я«хЯ«ЪЯ«┐Я«хЯ««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«ЙЯ«цЯ»Ђ. Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї p Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї q Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»ЄЯ«»Я»іЯ«┤Я«┐Я«» Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«ЙЯ«цЯ»Ђ.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ:
Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ«┐Я«▓Я»Ї Я«хЯ»ѕЯ«цЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«» Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«» Я««Я»ЂЯ«ЪЯ«┐Я«хЯ«┐Я«ЕЯ»ѕ (Я««Я»єЯ«»Я»ЇЯ«фЯ»ЇЯ«фЯ«┐Я«ЕЯ»ЇЯ«▒Я«┐) Я«еЯ«ЙЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Рђўa' Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Рѕџb Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Є:
(i) a + Рѕџb; (ii) a Рѕњ Рѕџb; (iii) aРѕџb; (iv) a/Рѕџb (v) Рѕџb/a
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї 4 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї Рѕџ5 Я«љ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї 4 +Рѕџ5 , 4 Рѕњ Рѕџ5 , 4Рѕџ5 , 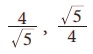 РђдРђд Я«ЄЯ«хЯ»ѕ Я«јЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Є.
РђдРђд Я«ЄЯ«хЯ»ѕ Я«јЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Є.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.11
0.5151151115, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 0.5353353335.... Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ѕЯ«»Я»Є Я«јЯ«хЯ»ѕЯ«»Я»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«ЄЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ѕЯ«»Я»Є Я«ЅЯ«│Я»ЇЯ«│ Я«ЄЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї 0.5152 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 0.5352 Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.12
Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«БЯ»ЇЯ«ЪЯ«хЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»Ї x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«Й Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«Й Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
(i) a = 2+Рѕџ3 , b = 2 Рѕњ Рѕџ3 ; x = a + b, y = a Рѕњ b
(ii) a = Рѕџ2+7, b = Рѕџ2 Рѕњ 7; x = a + b, y = a Рѕњ b
(iii) a = Рѕџ75, b = Рѕџ3 ; x = ab, y = a/b
(iv) a = Рѕџ18 , b = Рѕџ3; x = ab, y = a/b
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
(i) a = 2+Рѕџ3, b = 2 Рѕњ Рѕџ3 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
x = a + b = (2 + Рѕџ3) + (2 Рѕњ Рѕџ3) = 4, Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї.
y = a Рѕњ b = (2 + Рѕџ3) Рѕњ (2 Рѕњ Рѕџ3) = 2Рѕџ3 Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї.
(ii) a = Рѕџ2 +7 , b = Рѕџ2Рѕњ7 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
x = a + b = (Рѕџ2 +7 ) +(Рѕџ2Рѕњ7) = 2Рѕџ2 Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї.
y = a Рѕњ b = (Рѕџ2 +7 ) Рѕњ (Рѕџ2Рѕњ7) = 14 Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї.
(iii) a = Рѕџ75, b = Рѕџ3 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
x = ab = Рѕџ75 ├Ќ Рѕџ3 = Рѕџ[75 ├Ќ 3] = Рѕџ[5├Ќ5├Ќ3├Ќ3] = 5├Ќ3=15 Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї.
y = a/b = Рѕџ75 / Рѕџ3 = Рѕџ[75/3] = Рѕџ25 = 5 Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї.
(iv) a = Рѕџ18, b = Рѕџ3 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ»Ђ.
x = ab = Рѕџ18├ЌРѕџ3 = Рѕџ[18├Ќ3] = Рѕџ[6├Ќ3├Ќ3] = 3Рѕџ6 Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї.
y = a/b = Рѕџ18/Рѕџ3 = Рѕџ[18/3] = Рѕџ6 Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї.
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ:
Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЄЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї, Я«ЋЯ«┤Я«┐Я«цЯ»ЇЯ«цЯ«▓Я»Ї, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї, Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«єЯ«ЋЯ«┐Я«»Я«Е Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«ЋЯ«хЯ»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«ЋЯ«хЯ»І Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»єЯ«│Я«┐Я«хЯ«ЙЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
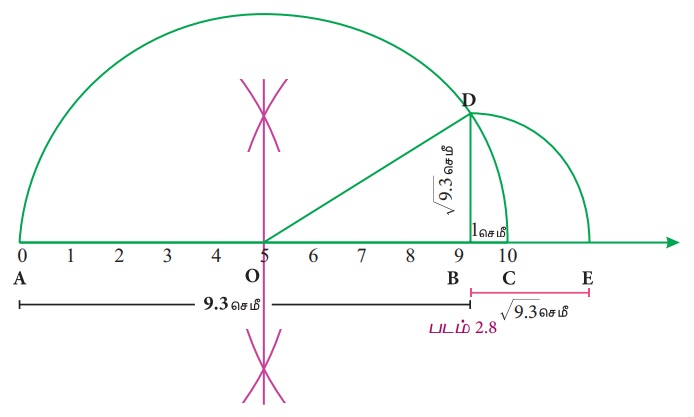
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.13
Рѕџ9.3 Я«љ Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
Рђб Я«њЯ«░Я»Ђ Я«еЯ»ЄЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«цЯ«┐Я«▓Я»Ї A Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Рђб AB = 9.3 Я«џЯ»єЯ««Я»ђ Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ B Я«јЯ«ЕЯ»ЇЯ«▒ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Рђб BC = 1 Я«џЯ»єЯ««Я»ђ Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЁЯ«▓Я«ЋЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«цЯ»ѕ РђўC' Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Рђб ACРѕњЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ѕЯ«»Я«ЋЯ»Ї Я«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я»ѕЯ«»Я«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕ O Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї.
Рђб O Я«љ Я««Я»ѕЯ«»Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї OC = OA Я«љ Я«єЯ«░Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЁЯ«░Я»ѕ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«»Я«хЯ»ЂЯ««Я»Ї.
Рђб ABРѕњЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ«Ћ B Я«ЄЯ«▓Я»Ї BD Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЋЯ»ІЯ«ЪЯ»Ђ Я«хЯ«░Я»ѕЯ«»Я«хЯ»ЂЯ««Я»Ї.
Рђб Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ, BD = Рѕџ9.3 Я«ЄЯ«цЯ»ѕ Я«јЯ«БЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї BE = BD = Рѕџ9.3 Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.