நினைவு கூர்வதற்கான கருத்துகள்

நினைவு கூர்வதற்கான கருத்துகள்

• p/q, q≠0 என்ற வடிவில் உள்ள எண்ணின் தசம விரிவானது முடிவு பெறும் எனில், p/q இன் தசம விரிவு முடிவுறு தசமவிரிவு (Terminating decimal expansion) எனப்படும். முடிவுறு தசம விரிவினைக் கொண்ட எண் முடிவுறு தசம எண் எனப்படும் 

• p/q, q ≠ 0 என்ற எண்ணின் தசம விரிவு காணும்போது எந்நிலையிலும் மீதி பூச்சியமாகவில்லை எனில், ஈவில் மீண்டும் மீண்டும் வரும் இலக்கங்களின் தொகுதி கிடைக்கும். இந்நிலையில் p/q இன் தசம விரிவு முடிவுறாச் சுழல் தசம விரிவு (Non terminating and recurring decimal expansion) எனப்படும். முடிவுறாச் சுழல் தசம விரிவினைக் கொண்ட எண் முடிவுறாச் சுழல் தசம எண் எனப்படும்.

• p/q, q ≠ 0 வடிவில் உள்ள விகிதமுறு எண்ணை p / [2m × 5n] (p∈ℤ மற்றும் m, n ∈ W) என்ற வடிவில் எழுத முடியுமானால், அந்த விகிதமுறு எண் முடிவுறு தசம விரிவினைப் பெற்றிருக்கும். அவ்வாறில்லையெனில், அந்த விகிதமுறு எண் முடிவுறாச் சுழல் தசம விரிவினைப் பெற்றிருக்கும் 

• ஒரு விகிதமுறு எண்ணினை முடிவுறு தசம விரிவாகவோ அல்லது முடிவுறாச் சுழல் தசம விரிவாகவோ குறிப்பிடலாம்.

• முடிவுறாச் சுழல் தன்மையற்ற தசம விரிவினைக் கொண்ட எண் ஒரு விகிதமுறா எண் ஆகும். எனவே, ஒரு விகிதமுறா எண்ணை p/q (p, q முழுக்கள் மற்றும் q ≠ 0) என்ற வடிவில் எழுதமுடியாது. 

• மெய்யெண்களின் கணமானது விகிதமுறு மற்றும் விகிதமுறா எண்களின் சேர்ப்புக் கணமாகும்.

• ஒவ்வொரு மெய்யெண்ணும் ஒரு விகிதமுறு எண்ணாகவோ அல்லது விகிதமுறா எண்ணாகவோ இருக்கும். 

• ஒரு மெய்யெண் விகிதமுறு எண் அல்ல எனில், அது ஒரு விகிதமுறா எண்ணாகும்.

• a என்பது மிகை விகிதமுறு எண், n ஒரு மிகை முழு மற்றும் n√a ஒரு விகிதமுறா எண் எனில், n√a என்பது ஒரு முறுடு எனப்படும்.

•  m, n என்பன மிகை முழுக்கள், a, b என்பன மிகை விகிதமுறு எண்கள் எனில்,

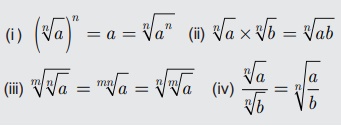
• ஒரு முறுடை மற்றொரு முறுடால் பெருக்கி விகிதமுறு எண்ணைப் பெறும் செயல்முறை விகிதப்படுத்துதல் எனப்படும்.

• N என்ற எண்ணை N = a×10n என எழுதலாம். இங்கே , 1 ≤ a < 10, (n ஒரு முழு ) என்றவாறு குறித்தல் அறிவியல் குறியீடு எனப்படும்.

இணையச் செயல்பாடு−1

இறுதியில் கிடைக்கப்பெறும் படம்

படி−1 கீழே கொடுக்கப்பட்டிருக்கும் உரலியைத் தேடுபொறியில் தட்டச்சு செய்க அல்லது துரிதத் துலங்கள் குறியீட்டை ஸ்கேன் செய்க.

படி−2 “Real Numbers” என்று GeoGebra பக்கத்தில் தோன்றும். இப்பக்கத்தில் பல பணித்தாள்கள் காணப்படும். புதிய கணக்குகளைச் செய்து பார்க்க “Square root spiral − 1st part” என்பதைச் சொடுக்கவும்.

படி−3 Steps எனும் நழுவலை இழுக்கவும். படிப்படியாக 2,3,4,5 என்ற எண்களின் வர்க்கமூல வடிவம் தோன்றும்.

படி−4 "Unit segment” எனும் நழுவலை இழுப்பதால் வர்க்கமூல வடிவத்தைப்பெரிதாகவும் தெளிவாகவும் காணலாம்.

செயல்பாட்டிற்கான உரலி : வர்க்க மூலம் : https://www.ggbm.at/m6GQc6mQ

இணையச் செயல்பாடு−2

செயல்பாட்டின் இறுதியில் கிடைக்கப்பெறுவது

படி − 1: கீழ்க்காணும் உரலி / விரைவுக் குறியீட்டைப் பயன்படுத்தி GeoGebra வின் "Real Numbers" என்னும் பணித்தாளின் பக்கத்திற்குச் செல்க. இப்பணித்தாளில் 

1. Rationalising the denominator for surds 

2. Law of exponents ஆகிய இரண்டு செயல்பாடுகள் கொடுக்கப்பட்டிருக்கும்.

முதல் செயல்பாட்டில், காரணிப்படுத்துவதற்கான வகுத்திகளும் எடுத்துக்காட்டுகளும் கொடுக்கப்பட்டிருக்கும். மேலும் கொடுக்கப்பட்டிருக்கும் கட்டங்களில் a மற்றும் b இன் மதிப்புகளை உள்ளீடு செய்தோ மதிப்புகளை மாற்றியோ காரணிகளின் மதிப்புகளை அறிக.

படி − 2 : இரண்டாம் செயல்பாட்டில் அடுக்கு விதி கொடுக்கப்பட்டிருக்கும். மேலும் வலப்பக்கத்தில் எடுத்துக்காட்டுகள் கொடுக்கப்பட்டிருக்கும். மதிப்புகளை மாற்றுவதற்கு m மற்றும் n நழுவல்களை நகர்த்தி, விடைகளைச் சரிபார்க்கவும்

செயல்பாட்டிற்கான உரலி : https://ggbm.at/BYEWDpHU or Scan the QR Code.