Я«хЯ«░Я»ѕЯ«»Я«▒Я»Ђ, Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ, Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ | Я«ЋЯ«Б Я««Я»іЯ«┤Я«┐ | Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї (Irrational Numbers) | 9th Maths : UNIT 2 : Real Numbers
9 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 2 : Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї
Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї (Irrational Numbers)
Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї (Irrational Numbers)
Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЂЯ«░Я«┐Я«» Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї, Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«фЯ»Ї Я«фЯ«БЯ»ЇЯ«фЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«»Я»ЂЯ««Я»Ї Я«еЯ»ђЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«ЕЯ»ЇЯ«фЯ»Є Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я»ђЯ«░Я»ЇЯ«ЋЯ«│Я»Ї. Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ЂЯ««Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«еЯ«┐Я«░Я«фЯ»ЇЯ«фЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│Я«ЕЯ«хЯ«Й? Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ»ЄЯ«▒Я»Ђ Я«јЯ«хЯ»ѕЯ«»Я»ЄЯ«ЕЯ»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«Е Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«ЕЯ«хЯ«Й Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«еЯ«ЙЯ««Я»Ї Я«єЯ«░Я«ЙЯ«»Я»ЇЯ«хЯ»ІЯ««Я»Ї.
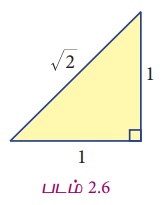
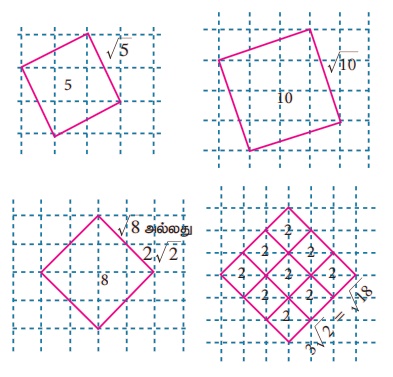
Я«ЊЯ«░Я»Ї Я«ЁЯ«▓Я«ЋЯ»Ђ Я«ЁЯ«│Я«хЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«њЯ«░Я»Ї Я«ЄЯ«░Я»ЂЯ«џЯ««Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ«џЯ»Ї Я«џЯ»єЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«Б Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ІЯ«БЯ«цЯ»ЇЯ«цЯ»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ»ІЯ««Я»Ї. Я«фЯ«┐Я«цЯ«ЙЯ«ЋЯ«░Я«ИЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ«░Я»ЇЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я«цЯ»ЇЯ«цЯ»ѕ Рѕџ[12 + 12] = Рѕџ2 (Я«фЯ«ЪЯ««Я»Ї 2.6 ) Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї. Я«ЋЯ«┐Я«░Я»ЄЯ«ЋЯ»ЇЯ«ЋЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Рѕџ2 Я«љ Я«њЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ»ЂЯ««Я«▓Я»ЇЯ«▓, Я«џЯ«ЙЯ«цЯ«ЙЯ«░Я«БЯ«фЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ««Я»ЂЯ««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓ Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«┐Я«ЪЯ«┐Я«цЯ»ЇЯ«цЯ«ЕЯ«░Я»Ї. Я«јЯ«БЯ»ЇЯ«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«Е Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»Ђ Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«» Я«еЯ««Я»ЇЯ«фЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ Я«ЄЯ«цЯ«ЕЯ«ЙЯ«▓Я»Ї Я«цЯ«ЋЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ«цЯ»Ђ. Рѕџ2 Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Я«ЄЯ«░Я»Ђ Я««Я»ЂЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я«ЙЯ«Ћ Я«јЯ«┤Я»ЂЯ«ц Я«ЄЯ«»Я«▓Я«ЙЯ«ц Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Є Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї,
1. Рѕџ2 Я«љЯ«цЯ»Ї Я«цЯ«хЯ«┐Я«░, Я«ЁЯ«цЯ»ѕЯ«фЯ»ЇЯ«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»ЇЯ«БЯ«▒Я»ЇЯ«▒ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ: Рѕџ5 , Рѕџ7, 2Рѕџ3 ,...
2. ¤ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я«│Я«хЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї, Я«ЁЯ«цЯ«ЕЯ»Ї Я«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЊЯ«░Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
3. e Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«єЯ«»Я»ЇЯ«▓Я«░Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»Ї Я«јЯ«Е Я«ЁЯ«▒Я«┐Я«»Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»ЂЯ«хЯ»ЂЯ««Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЊЯ«░Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
4. Я«цЯ«ЎЯ»ЇЯ«Ћ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ«ЎЯ»ЇЯ«Ћ Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«цЯ«ЎЯ»ЇЯ«ЋЯ«фЯ»Ї Я«фЯ«┐Я«░Я«┐Я«хЯ»Ђ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
Я«љЯ«ЎЯ»ЇЯ«ЋЯ»ІЯ«БЯ««Я»Ї, Я«љЯ«ЎЯ»ЇЯ«ЋЯ«░Я««Я»Ї, Я«цЯ«џЯ«« Я«ЋЯ»ІЯ«БЯ««Я»Ї, Я«фЯ«ЕЯ»ЇЯ«ЕЯ«┐Я«░Я»ЂЯ««Я»ЂЯ«ЋЯ«┐ Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«јЯ«│Я«┐Я«» Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї Я«цЯ»ѓЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ«цЯ»Ї Я«цЯ«ЪЯ»ЂЯ««Я«ЙЯ«▒Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«цЯ«ЎЯ»ЇЯ«Ћ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЄЯ«цЯ»ЂЯ«хЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«цЯ«ЎЯ»ЇЯ«Ћ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї (1 : 1.6)
Я«цЯ«ЎЯ»ЇЯ«Ћ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЋЯ«▓Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«ЪЯ»ЇЯ«ЪЯ«ЪЯ«ЋЯ»Ї Я«ЋЯ«▓Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«џЯ«┐Я«▒Я«еЯ»ЇЯ«ц Я«ЁЯ«▒Я»ЇЯ«фЯ»ЂЯ«ц Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ»ІЯ«▒Я»ЇЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
(a + b) Я«еЯ»ђЯ«│Я««Я»ЂЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»ѕ Я«ЄЯ«░Я»Ђ Я«цЯ»ЂЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Ћ (a Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b) Я«фЯ«┐Я«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї. Я«ЁЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«фЯ«┐Я«░Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, (a + b)РѕњЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї aРѕњЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»Ї aРѕњЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї bРѕњЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я»ЄЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«џЯ««Я««Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї.
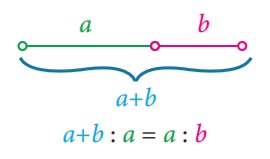
a + b : a = a : b
Я«ЄЯ«цЯ»ѕ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ«џЯ»Ї Я«џЯ««Я««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒Я«▓Я«ЙЯ««Я»Ї. (a+b) / a = a/b
Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ a Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ a + b Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї b Я«ЄЯ«ЕЯ»Ї Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
1. Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї (Irrational Numbers on the Number Line)
Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«░Я«┐Я«» Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я»Ї Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«јЯ«ЎЯ»ЇЯ«ЋЯ»ЂЯ«│Я»ЇЯ«│Я«Е?
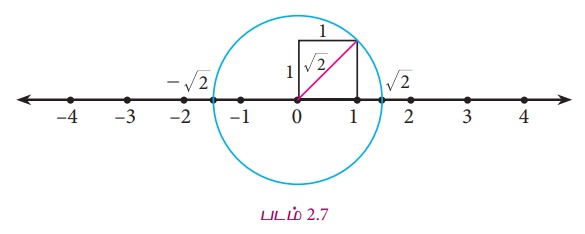
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ, Рѕџ2 Я«љ Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«ЄЯ«цЯ»Ђ Я«јЯ«│Я«┐Я«цЯ»Ђ.
Рѕџ2 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЊЯ«░Я«▓Я«ЋЯ»Ђ Я«еЯ»ђЯ«│Я««Я»ЂЯ«ЪЯ»ѕЯ«» Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я»ѕЯ«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«еЯ»ђЯ«│Я««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«Ћ. (Я«јЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐?) Я«ЄЯ«еЯ»ЇЯ«ц Я«ЁЯ«│Я«хЯ«┐Я«▓Я»Ї Я«ЊЯ«░Я»Ї Я«јЯ«│Я«┐Я«» Я«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ»ѕ Я«хЯ«░Я»ѕЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я»ѕЯ«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕ Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕЯ«ЋЯ»Ї (Я«фЯ«ЪЯ««Я»Ї 2.7) Я«ЋЯ«ЙЯ«БЯ«▓Я«ЙЯ««Я»Ї.
Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«▓Я»Ї 0 Я«љ Я««Я»ѕЯ«»Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї, Я«џЯ«цЯ»ЂЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я»ѕ Я«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ»ѕ Я«єЯ«░Я««Я«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«њЯ«░Я»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«Ћ. Я«ЁЯ«цЯ»Ђ Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«ЄЯ«░Я»Ђ Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. 0 Я«хЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«▓Я«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я«ЙЯ«Ћ Рѕџ2 Я«хЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я««Я«ЙЯ«Ћ РѕњРѕџ2 Я«хЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«хЯ»єЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ«хЯ»ЂЯ««Я»Ї. (Рѕџ2 Я«љЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«цЯ»Ї Я«цЯ»ЂЯ«хЯ«ЎЯ»ЇЯ«ЋЯ«┐ Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї РѕњРѕџ2 Я«љЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«цЯ»ЇЯ«цЯ«ЙЯ«ЋЯ«┐ Я«хЯ«┐Я«ЪЯ»ЇЯ«ЪЯ«цЯ»Ђ)
Я«ЄЯ«»Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«▓Я»Ї Я«цЯ»ЂЯ«хЯ«ЎЯ»ЇЯ«ЋЯ«┐ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«░Я»ѕ Я«хЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐, Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї. Я«ЄЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«хЯ«┐Я«░Я«┐Я«хЯ»ЂЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐, Я«хЯ»ЄЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«Б Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я«Й? Я«єЯ««Я»Ї. Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«ЅЯ«»Я«░Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЋЯ«▒Я»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«цЯ»Ї Я«цЯ«џЯ«« Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«цЯ»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«хЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«ЅЯ«цЯ«хЯ«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«еЯ«ЙЯ««Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«ЪЯ«┐Я«хЯ«цЯ»ЇЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
2. Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї (Decimal Representation of a Rational Number)
Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ»ѕЯ«фЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ««Я«ЙЯ«Ћ Я«јЯ«┤Я»ЂЯ«цЯ«┐Я«ЕЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«цЯ«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«ЪЯ«┐Я«хЯ»ѕ Я«еЯ»ђЯ«│Я»ЇЯ«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«фЯ»єЯ«▒Я«▓Я«ЙЯ««Я»Ї. Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«јЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»ЂЯ««Я»Ї Я««Я»ђЯ«цЯ«┐ 0 Я«хЯ«░Я»ЂЯ«хЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЂЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї:
Я«хЯ«░Я»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ«цЯ»Ї Я«цЯ«ЙЯ«│Я«┐Я«▓Я»Ї Я«џЯ«цЯ»ЂЯ«░Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕ Я«хЯ«░Я»ѕЯ«еЯ»ЇЯ«цЯ»Ђ Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я«ЁЯ«│Я«хЯ«┐Я«▓Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«ЅЯ«░Я»ЂЯ«хЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я«џЯ«┐Я«▓ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ,

Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«џЯ»єЯ«»Я«▓Я«ЙЯ«ЕЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я«ЙЯ«Е Я«цЯ«џЯ«« Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»ЂЯ««Я»Ї. Я«ЄЯ«хЯ»ѕ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЕЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ««Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я«Й? Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї (Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я««Я«▒Я»ЇЯ«▒ Я««Я»ђЯ«цЯ«┐Я«ЋЯ«│Я»Ї) Я«ЄЯ«цЯ»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ«ЙЯ«Е Я«цЯ»єЯ«│Я«┐Я«хЯ»ѕ Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.2
Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ«хЯ«ЕЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«цЯ»Ї Я«цЯ«џЯ««Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«Ћ. (i) Рѕњ4/11 (ii) 11/75
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ

Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ:
Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЕЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»Ђ Я«фЯ»єЯ«▒Я«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ. Я««Я»ђЯ«цЯ«┐ Я«хЯ«░Я»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я»ђЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я««Я»ђЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«░Я»ЂЯ««Я»Ї. Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«ц Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.
Я«јЯ«ЕЯ«хЯ»Є, Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«ЕЯ«цЯ»Ђ,
(i) Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»ЂЯ««Я»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ«хЯ»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ
(ii) Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЋЯ«хЯ»І Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«цЯ«ЕЯ»Ї Я««Я«▒Я»ЂЯ«цЯ«▓Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я»Є. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, Я«ЊЯ«░Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«ЕЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»ЇЯ«▒Я»І Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ«ЙЯ«ЋЯ«хЯ»І Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«ЁЯ«хЯ»ЇЯ«хЯ»єЯ«БЯ»Ї Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
3. Я«цЯ«џЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЙЯ«▓Я««Я»ЂЯ«▒Я»ѕЯ««Я»ѕ (Period of Decimal)
Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ«џЯ««Я«хЯ«┐Я«░Я«┐Я«хЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«» Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»Є Я«ЁЯ«хЯ»ЇЯ«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЕЯ»Ї Я«цЯ«џЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЙЯ«▓ Я««Я»ЂЯ«▒Я»ѕЯ««Я»ѕ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ,
(i) 
Я«ЄЯ«цЯ«ЕЯ»Ї Я«ЋЯ«ЙЯ«▓ Я««Я»ЂЯ«▒Я»ѕЯ««Я»ѕ = 6
(ii) = 
Я«ЄЯ«цЯ«ЕЯ»Ї Я«ЋЯ«ЙЯ«▓ Я««Я»ЂЯ«▒Я»ѕЯ««Я»ѕ = 2
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.3
1/3 Я«ЄЯ«ЕЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ 1/27 Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЕЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ. Я«ЄЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ 59/27 Я«ЄЯ«ЕЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«Ћ.
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
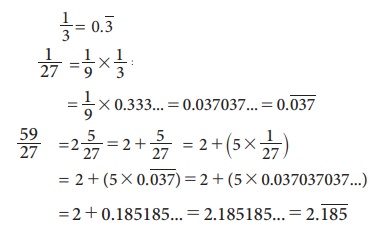
Я«ЄЯ«»Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ«▓Я»ѕЯ«ЋЯ»ђЯ«┤Я«┐Я«ЋЯ«│Я»Ї Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Є. Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«ЪЯ«┐Я«хЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«єЯ«░Я»ЇЯ«хЯ««Я»ѓЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«фЯ«хЯ»ѕ. Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я««Я»ЂЯ«цЯ«▓Я»Ї Я«фЯ«цЯ»ЇЯ«цЯ»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
4. Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«цЯ«▓Я»Ї (Conversion of Terminating Decimals into Rational Numbers)
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Е 2.945Я«љ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«Е Я«хЯ«ЪЯ«┐Я«хЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я««Я«ЙЯ«▒Я»ЇЯ«▒ Я««Я»ЂЯ«»Я«▓Я»ЇЯ«хЯ»ІЯ««Я»Ї.

(Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▓Я»Ї Я«еЯ»ЄЯ«░Я«ЪЯ«┐Я«»Я«ЙЯ«Ћ 2.945 = 2945/1000 Я«јЯ«Е Я«јЯ«┤Я»ЂЯ«ц Я«ЄЯ«»Я«▓Я»ЂЯ««Я«Й?)
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.4
Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«цЯ«џЯ«« Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ p/q (pЯ««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї q Я««Я»ЂЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї q РЅа 0) Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я««Я«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«Ћ:
(i) 0.35 (ii) 2.176 (iii) Рѕњ 0.0028
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
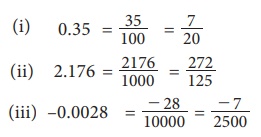
5. Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«џЯ«« Я«јЯ«БЯ»ЇЯ«БЯ»ѕ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«цЯ«▓Я»Ї (Conversion of NonРѕњterminating and recurring decimals into Rational Numbers)
Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«јЯ«БЯ»ЇЯ«БЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѕЯ«»Я«ЙЯ«│Я»ЂЯ«хЯ«цЯ»Ђ Я«јЯ«│Я«┐Я«цЯ»Ђ. 2.4Я«љЯ«фЯ»Ї Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«цЯ«џЯ«« Я«јЯ«БЯ»Ї Я«хЯ«░Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ«џЯ««Я«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«»Я»ѕ Я«еЯ»ђЯ«ЋЯ»ЇЯ«Ћ Я«ЁЯ«еЯ»ЇЯ«ц Я«јЯ«БЯ»ЇЯ«БЯ»ѕ 10Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЁЯ«цЯ«ЙЯ«хЯ«цЯ»Ђ, 2.4 = 24/10, Я«ЄЯ«цЯ»ѕЯ«џЯ»Ї Я«џЯ»ЂЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ«ЙЯ«▓Я»Ї 12/5 Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«цЯ»Є Я«цЯ«џЯ«« Я«јЯ«БЯ»Ї ![]() Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«▒Я»ЇЯ«▒ Рђю4РђЮ Я«хЯ«░Я»ЂЯ«хЯ«цЯ«ЙЯ«▓Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ«▒Я»ЇЯ«▒ Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«░Я»ЂЯ««Я»Ї.
Я«јЯ«Е Я«ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«▒Я»ЇЯ«▒ Рђю4РђЮ Я«хЯ«░Я»ЂЯ«хЯ«цЯ«ЙЯ«▓Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ«▒Я»ЇЯ«▒ Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«░Я»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ,
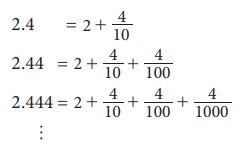
Я«јЯ«БЯ»ЇЯ«БЯ«▒Я»ЇЯ«▒ "4" Я«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Ђ Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѕЯ«»Я«ЙЯ«│Я»ЂЯ«хЯ«цЯ»Ђ Я«ЋЯ«ЪЯ«┐Я«ЕЯ««Я»Ї. Я«ЄЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«▒Я»ЇЯ«▒ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«░Я»ЂЯ«хЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«јЯ«хЯ»ЇЯ«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я«ЙЯ«хЯ«цЯ»Ђ Я«еЯ«ЙЯ««Я»Ї Я«хЯ«┐Я«ЪЯ»ЂЯ«фЯ«Ъ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«ЄЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«њЯ«ЕЯ»ЇЯ«▒Я»Ђ, Я«ЄЯ«░Я«БЯ»ЇЯ«ЪЯ»Ђ, Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«еЯ»ђЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ«ЙЯ«▓Я»ЂЯ««Я»Ї Я«ЁЯ«цЯ»ЇЯ«цЯ»іЯ«ЪЯ«░Я»І, Я«ЁЯ«цЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»І Я««Я«ЙЯ«▒Я«ЙЯ«цЯ»Ђ. Я«ЁЯ«цЯ»Є Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«цЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я«ЙЯ«Ћ Я«ЁЯ«цЯ»Ђ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.

(Я«ЄЯ«цЯ»ѕ 10 Я«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«цЯ«џЯ««Я«фЯ»Ї Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐ Я«ЊЯ«░Я»Ї Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«хЯ«▓Я«фЯ»ЇЯ«фЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«еЯ«ЋЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»ЂЯ««Я»Ї Я«ЄЯ«ЕЯ»ЇЯ«ЕЯ««Я»ЂЯ««Я»Ї 4 Я«јЯ«ЕЯ»ЇЯ«▒ Я«јЯ«БЯ»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ).
(2) Я«ЄЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ (1) Я«љЯ«ЋЯ»Ї Я«ЋЯ«┤Я«┐Я«ЋЯ»ЇЯ«Ћ,

x = 22/9, Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«цЯ»Є Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«фЯ«▒Я»ЇЯ«▒Я«┐ Я«јЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ««Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«▓Я«ЙЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.5
Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«цЯ«џЯ«« Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕ p/q (p,q Рѕѕ Z Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї q РЅа 0) Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я««Я«ЙЯ«▒Я»ЇЯ«▒Я»ЂЯ«Ћ.
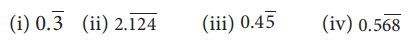
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
(i) x =![]() = 0.3333... Я«јЯ«ЕЯ»ЇЯ«Ћ (1)
= 0.3333... Я«јЯ«ЕЯ»ЇЯ«Ћ (1)
(Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«ЋЯ«ЙЯ«▓ Я««Я»ЂЯ«▒Я»ѕЯ««Я»ѕ = 1 Я«јЯ«ЕЯ«хЯ»Є, (1) Я«љ 10 Я«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«Ћ)
10 x = 3.3333... (2)
(2) Рѕњ (1): 9x = 3 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ x = 1/3
(ii) x = ![]() = 2.124124124... (1)
= 2.124124124... (1)
(Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«џЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЙЯ«▓ Я««Я»ЂЯ«▒Я»ѕЯ««Я»ѕ 3 Я«цЯ«џЯ«« Я«фЯ»ЂЯ«│Я»ЇЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«│Я»ЇЯ«│ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є (1) Я«љ 1000РѕњЯ«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«Ћ.)
1000 x = 2124.124124124... (2)
(2) Рѕњ (1): 999 x = 2122
x = 2122/999
(iii) x = ![]() = 0.45555... (1)
= 0.45555... (1)
(Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ (1) Я«љ 10РѕњЯ«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«Ћ.)
10 x = 4.5555... (2)
(Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«џЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЙЯ«▓ Я««Я»ЂЯ«▒Я»ѕЯ««Я»ѕ 1, Я«јЯ«ЕЯ«хЯ»Є (2) Я«љ 10 Я«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«Ћ.)
100 x = 45.5555... (3)
(3) Рѕњ (2): 90 x = 41 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x = 41/90
(iv) x = ![]() = 0.5686868..... (1)
= 0.5686868..... (1)
(Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ (1) Я«љ 10РѕњЯ«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«Ћ.)
10 x = 5.686868.... (2)
(Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ Я«цЯ«џЯ««Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ«ЙЯ«▓ Я««Я»ЂЯ«▒Я»ѕЯ««Я»ѕ 2, Я«јЯ«ЕЯ«хЯ»Є (2) Я«љ 100РѕњЯ«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«Ћ.)
1000 x = 568.686868... (3)
(3) Рѕњ (2): 990 x = 563 Я«ЁЯ«▓Я»ЇЯ«▓ Я«цЯ»Ђ x = 563/990
Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ»Ђ
(i) Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«ЪЯ«┐Я«хЯ««Я»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«Й Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«Й Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«Й Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«хЯ«┐Я«цЯ«┐Я«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЁЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї.
(ii) Я«њЯ«░Я»Ђ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї p/q, qРЅа0 Я«љ 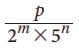 Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«ц Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї, Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ p Рѕѕ Z Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї m, n Рѕѕ W, Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«хЯ»ЇЯ«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«ц Я«ЄЯ«»Я«▓Я«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«» Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«ц Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї, Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ p Рѕѕ Z Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї m, n Рѕѕ W, Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«хЯ«┐Я«ЋЯ«┐Я«цЯ««Я»ЂЯ«▒Я»Ђ Я«јЯ«БЯ»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«јЯ«БЯ»ЇЯ«БЯ«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЁЯ«хЯ»ЇЯ«хЯ«ЪЯ«┐Я«хЯ«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«ц Я«ЄЯ«»Я«▓Я«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ Я«јЯ«ЕЯ«┐Я«▓Я»Ї Я«ЁЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«» Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.6
Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЙЯ««Я«▓Я»Ї Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«»Я»ЂЯ«ЪЯ»ѕЯ«»Я«Е Я«јЯ«Е Я«хЯ«ЋЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«Ћ:
(i) 13/64 (i) Рѕњ71/125 (iii) 43/375 (iv) 31/400
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
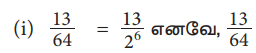 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
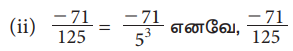 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї..
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї..
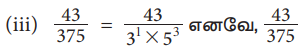 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«џЯ»Ї Я«џЯ»ЂЯ«┤Я«▓Я»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
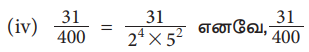 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї...
Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЇЯ«▒Я«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї...
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»Ђ 2.7
Я«џЯ«░Я«┐Я«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«Ћ ![]()
Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ
x =![]() = 0.99999... (1)
= 0.99999... (1)
(Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ (1) Я«љ 10 Я«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ)
10 x = 9.99999... (2)
(2) Я«ЄЯ«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ (1) Я«љЯ«ЋЯ»Ї Я«ЋЯ«┤Я«┐Я«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї
9x = 9 Я«ЁЯ«▓Я»ЇЯ«▓ Я«цЯ»Ђ x =1
![]() = 1
= 1
1 = 0.9999...
7 = 6.9999...
3.7 = 3.6999....
Я«ЄЯ«хЯ»ЇЯ«хЯ«ЪЯ«┐Я«хЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ, Я«јЯ«еЯ»ЇЯ«цЯ«хЯ»іЯ«░Я»Ђ Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я»Ђ Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я««Я»ЂЯ«ЪЯ«┐Я«хЯ»ЂЯ«▒Я«ЙЯ«цЯ»Ї Я«цЯ«џЯ«« Я«хЯ«┐Я«░Я«┐Я«хЯ«ЙЯ«Ћ Рђю9РђЮ Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»іЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Ћ Я«јЯ«┤Я»ЂЯ«ц Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«ЁЯ«▒Я«┐Я«»Я«▓Я«ЙЯ««Я»Ї.