எடுத்துக்காட்டு கணக்குகள் - வகைமை (வகையிடல் தன்மை) மற்றும் தொடர்ச்சி (Differentiability and Continuity) | 11th Mathematics : UNIT 10 : Differential Calculus: Differentiability and Methods of Differentiation

11 வது கணக்கு : அலகு 10 : வகை நுண்கணிதம் வகைமை மற்றும் வகையிடல் முறைகள் DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION

வகைமை (வகையிடல் தன்மை) மற்றும் தொடர்ச்சி (Differentiability and Continuity)

ஒரு சார்புக்கு ஒரு புள்ளியில் தொடர்ச்சித் தன்மை உள்ளதாலேயே அச்சார்பு அப்புள்ளியில் வகைமையாக இருக்கும் எனக் கூற இயலாது.

விளக்க எடுத்துக்காட்டு 10.3

x = 2 என்ற புள்ளியில் ƒ(x) = |x - 2| எனும் சார்பின் வகைமைத் தன்மையைச் சோதிக்க.

தீர்வு

இச்சார்பு x = 2-ல் தொடர்ச்சியானது என்பதை அறிவோம். ஆனால்,

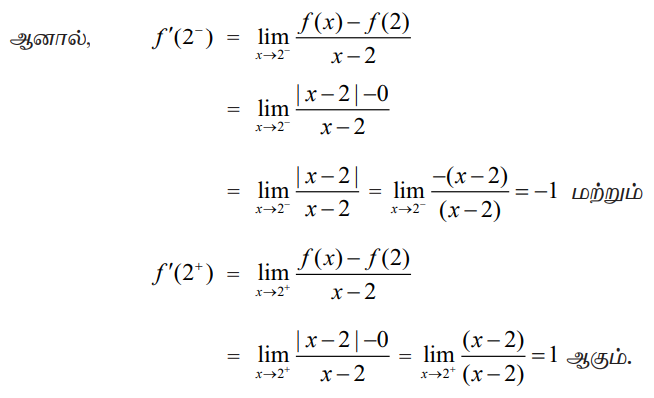
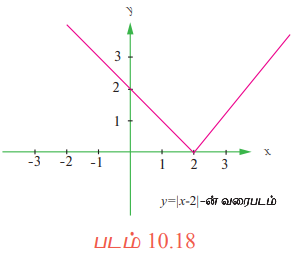
இங்கு இடப்பக்க மற்றும் வலப்பக்க வகைக்கெழுக்களான ƒ′(2-) மற்றும் ƒ'(2+) ஆகியவை சமமற்றவை என்பதால், ƒ′ (2) கிடைக்கப்பெறாது. அதாவது, x = 2-ல் ƒ என்ற சார்பு வகையிடத்தக்கதல்ல. ஏனைய புள்ளிகளில் சார்பு வகைமையானது (வகையிடத்தக்கது) ஆகும்.

மேலும் x0 ≠ 2 எனும் மற்ற புள்ளிகளில்

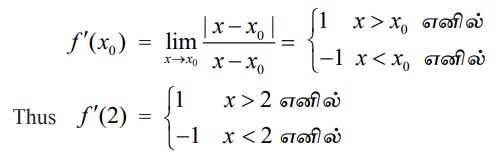
உண்மையில், ƒ′ (2) கிடைக்கப் பெறாது எனும் கருத்து வடிவியல் ரீதியாக வளைவரை y = |x - 2| -க்கு (2, 0) என்ற புள்ளியில் தொடுகோடு இல்லை என்பதன் மூலம் புலனாகிறது. மேலும் (2, 0) புள்ளியில் வளைவரை கூர்முனை கொண்டுள்ளதைக் கவனிக்க.

விளக்க எடுத்துக்காட்டு 10.4

x = 0 என்ற புள்ளியில் ƒ(x) = x1/3 -ன் வகைமைத் தன்மையைக் காண்க.

தீர்வு

ƒ(x) = x1/3 என்க. இச்சார்பின் வளைவரையில் எவ்வித துவாரமோ (அல்லது) உடைப்போ இல்லை என்பதால் சார்பகத்தில் உள்ள அனைத்துப் புள்ளிகளிலும் சார்பு தொடர்ச்சியாக இருக்கும்.

ƒ'(0) கிடைக்கப் பெறுமா எனச் சோதித்துப் பார்ப்போம்.

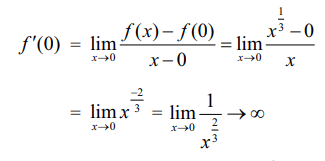
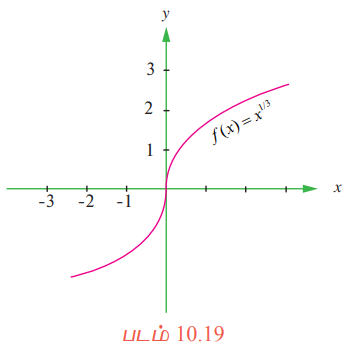
எனவே, x = 0-ல், ƒ(x)-க்கு வகைமை இல்லை, மேலும் x = 0-ல் தொடுகோடு செங்குத்துக் கோடாக உள்ளது (படம் 10.19). எனவே, x = 0-ல் ƒ-க்கு வகைமை இல்லை.

எடுத்துக்காட்டு 10.3

விளக்க எடுத்துக்காட்டு 10.5

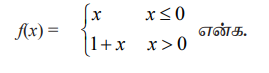
ƒ'(0) கிடைக்கப்பெறின் அதனைக் காண்க.

தீர்வு

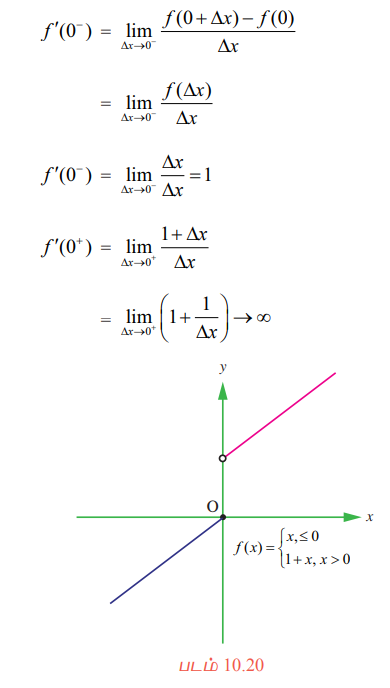
எனவே ƒ′ (0) கிடைக்கப்பெறாது.

இங்கு x = 0-ல் ƒ -க்கு ஒரு துள்ளல் (jump) உள்ளது. அதாவது x = 0 என்பது ஒரு துள்ளல் தொடர்ச்சியின்மையாகும்.

மேற்கண்ட விளக்க எடுத்துக்காட்டுகள் மற்றும் உதாரணங்கள் ஆகியவற்றிலிருந்து பின்வரும் முடிவகளைத் தொகுக்கலாம்.

ஒரு சார்பு ƒ ஆனது சார்பகத்திலுள்ள ஒரு புள்ளி x0-ல் கீழ்க்காணும் ஏதாவது ஒரு நிகழ்வு மெய் எனில், ƒ அப்புள்ளியில் வகைமையாகாது.

(i) x = x0 என்ற புள்ளியில் ƒ -க்கு செங்குத்துத் தொடுகோடு அமைகிறது.

(ii) x = x0 என்ற ஒரு கூர்முனைப்புள்ளியில் சந்திக்கிறது. (கூர்மையான V வடிவம் அல்லது கூர்மையான உச்சி Λ)

(iii) x = x0 என்ற புள்ளியில் ƒ ஆனது தொடர்ச்சியற்றது.

கீழ்க்காணும் நிகழ்வுகளில் ஒரு சார்பு வகைமை ஆகாது :

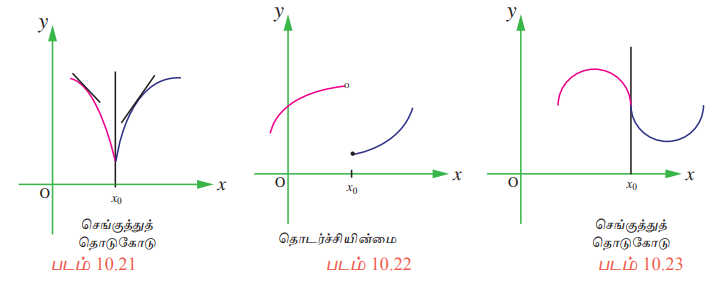
விளக்க எடுத்துக்காட்டு 10.3 மற்றும் 10.4-ல் சார்பு ƒ(x) = | x -2 | மற்றும் ƒ(x) = x1/3 முறையே x = 2 மற்றும் x = 0-ல் தொடர்ச்சியாகவும் ஆனால் அந்த இடங்களில் ƒ வகைமையற்றதாகவும் உள்ளது.

அதே நேரத்தில் 10.3 உதாரணத்திலும் 10.5 விளக்க எடுத்துக்காட்டிலும் உள்ள சார்புகள்

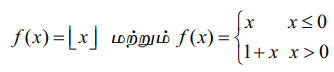ஆகும். முறையே எந்தவொரு முழு எண் x = n-க்கும் மற்றும் x = 0 -ல் தொடர்ச்சியற்றும் வகைமையில்லாமலும் அமைகின்றது. மேற்கண்ட ஆய்வைப் பின்வரும் வகையில் சுருக்கமாகக் கூறலாம் : தொடர்ச்சியின்மை வகைமையின்மையை கொடுக்கிறது.

தேற்றம் 10.1 (வகைமைத் தொடர்ச்சியை கொடுக்கிறது) (Differentiability implies continuity)

x = x0 என்ற புள்ளியில் ƒ வகைமையானால் அப்புள்ளியில் ƒ தொடர்ச்சியானதாக இருக்கும்.

நிரூபணம்

x0 எனும் புள்ளியைக் கொண்ட (a, b) என்ற இடைவெளியில் ƒ(x) வகைமையானது என்க. எனவே, 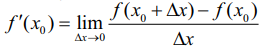கிடைக்கப்பெற்று ƒ'(x0) என்பது ஒரு முடிவுறு எண் என்பது புலனாகிறது

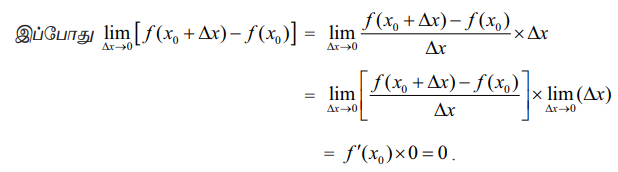
இதிலிருந்து x = x0 -ல் ƒ தொடர்ச்சியாக இருக்கிறது என்பது உண்மையாகிறது.

முதல் கொள்கையிலிருந்து வகைக்கெழு காணல் (Derivatives from first principle)

வகைக்கெழு வரையறைகளில் எடுத்துரைக்கப்பட்ட நிபந்தனைகளைப் பயன்படுத்தி ஒரு சார்பின் வகைக்கெழு காணும் வழிமுறையே முதல் கொள்கையிலிருந்து வகைக்கெழு காணல் என அழைக்கப்படுகிறது.

Tags : Solved Example Problems, Exercise | Mathematics எடுத்துக்காட்டு கணக்குகள்.

11th Mathematics : UNIT 10 : Differential Calculus: Differentiability and Methods of Differentiation : Differentiability and Continuity Solved Example Problems, Exercise | Mathematics in Tamil : 11th Standard Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 11 வது கணக்கு : அலகு 10 : வகை நுண்கணிதம் வகைமை மற்றும் வகையிடல் முறைகள் DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION : வகைமை (வகையிடல் தன்மை) மற்றும் தொடர்ச்சி (Differentiability and Continuity) - எடுத்துக்காட்டு கணக்குகள் : 11 ஆம் வகுப்பு புத்தகம் கேள்விகள் மற்றும் பதில்கள்.