11 Я«хЯ«цЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 10 : Я«хЯ«ЋЯ»ѕ Я«еЯ»ЂЯ«БЯ»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ««Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«ЪЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION
Я«хЯ«ЋЯ»ѕ Я«еЯ»ЂЯ«БЯ»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ««Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«ЪЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION
Я«ЁЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«ЙЯ«»Я««Я»Ї 10
Я«хЯ«ЋЯ»ѕ Я«еЯ»ЂЯ«БЯ»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ««Я»ѕ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«ЪЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»Ї
DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION

"Я«цЯ»ЄЯ«хЯ»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»Ї, Я«џЯ»єЯ«»Я»ЇЯ«хЯ«Е Я«џЯ»єЯ«»Я»Ї, Я«ЁЯ«ЪЯ»ѕЯ«»Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«»Я«цЯ»ѕ Я«ЁЯ«ЪЯ»ѕЯ«хЯ«ЙЯ«»Я»ЇРђЮ РђЊ Я«▓Я«┐Я«фЯ«┐Я«ЕЯ«┐Я«ЪЯ»ЇЯ«ИЯ»Ї
Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ««Я»Ї (Introduction)
Я«ЄЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐Я«»Я«┐Я«▓Я»Ї Я«хЯ«ЋЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«»Я«▓Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«»Я»ЂЯ««Я»Ї, Я«ЁЯ«цЯ«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ«ЙЯ«Е Я«ЄЯ«цЯ«░ Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«єЯ«░Я«ЙЯ«»Я»ЇЯ«хЯ«цЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«ЁЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«Ъ Я«хЯ«ЙЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«џЯ«хЯ«ЙЯ«▓Я»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«Б Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї. Я«ЄЯ«цЯ«ЕЯ»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«ЙЯ«Ћ Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«ЅЯ«цЯ«ЙЯ«░Я«БЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«цЯ»ѓЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЪЯ«ЋЯ»ЇЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я»ЂЯ«БЯ«░Я»ЇЯ«хЯ»Ђ Я««Я»ѓЯ«▓Я««Я»Ї Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«хЯ»ЄЯ«Ћ Я«хЯ»ђЯ«цЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«ЄЯ«»Я«▓Я»ЇЯ«фЯ»Ђ Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ Я«ЁЯ«ЕЯ»ѕЯ«хЯ«░Я«┐Я«ЪЯ««Я»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«цЯ»Ђ. Я«џЯ«ЙЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«Ћ Я«њЯ«░Я»Ђ Я««Я«БЯ«┐ Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«фЯ»ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 60 Я«ЋЯ«┐.Я««Я»ђ. Я«цЯ»ѓЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЪЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї Я«ЁЯ«фЯ»ЇЯ«фЯ»ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«цЯ»Ї Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я»Ї Я««Я«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ 60 Я«ЋЯ«┐.Я««Я»ђ. Я«јЯ«Е Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«фЯ«»Я«БЯ«цЯ»Ї Я«цЯ»ѓЯ«░Я««Я»Ї Я««Я»ЂЯ«┤Я»ЂЯ«хЯ«цЯ»ЂЯ««Я»Ї 60 Я«ЋЯ«┐.Я««Я»ђ. Я«јЯ«ЕЯ«џЯ»Ї Я«џЯ»ђЯ«░Я«ЙЯ«Е Я«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»ЄЯ«»Я»Є Я«фЯ»ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ Я«ЄЯ«»Я«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я«ЙЯ«цЯ»Ђ. Я«ЈЯ«ЕЯ»єЯ«ЕЯ«┐Я«▓Я»Ї Я«еЯ«ЋЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ»ЂЯ«▒Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«џЯ«▒Я»ЇЯ«▒Я»Є Я«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ Я«ЋЯ»ЂЯ«▒Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«фЯ«┐Я«▒ Я«хЯ«ЙЯ«ЋЯ«ЕЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«хЯ»ЂЯ««Я»Ї Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї. Я«хЯ»ЄЯ«▒Я»Ђ Я«џЯ»іЯ«▒Я»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«џЯ»іЯ«▓Я»ЇЯ«хЯ«цЯ»єЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«▓Я»Ї, Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«фЯ»ЇЯ«фЯ»іЯ«▒Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ»Ї Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я»Ї Я««Я«ЙЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«ЕЯ«▓Я«ЙЯ««Я»Ї.

Я«њЯ«░Я»Ђ Я«фЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«хЯ«░Я«цЯ»ЇЯ«цЯ»Ђ Я«еЯ«┐Я«▒Я»ЂЯ«хЯ«ЕЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ»ЇЯ«ЪЯ«хЯ«БЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«њЯ«░Я»Ђ Я«фЯ»ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЊЯ«░Я»Ї Я«іЯ«░Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ІЯ«░Я»Ї Я«іЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«▓ Я«њЯ«░Я»Ђ Я««Я«БЯ«┐ Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї 60 Я«ЋЯ«┐.Я««Я»ђ. Я«ЋЯ«ЪЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»єЯ«ЕЯ«┐Я«▓Я»Ї Я«фЯ»ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«»Я«БЯ«фЯ»ЇЯ«фЯ«ЙЯ«цЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«єЯ«ЎЯ»ЇЯ«ЋЯ«ЙЯ«ЎЯ»ЇЯ«ЋЯ»Є Я«ЈЯ«▒Я»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«еЯ»ЄЯ«░ Я«хЯ«┐Я«░Я«»Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«»Я»ЂЯ««Я»Ї, Я«хЯ»ЄЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я»ѕЯ«хЯ«┐Я«ЕЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЈЯ«ЕЯ»ѕЯ«» Я«ЄЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«ѕЯ«ЪЯ»ЂЯ«џЯ»єЯ«»Я»ЇЯ«» Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЕЯ»ѕ Я«ЊЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«еЯ«░Я»Ї Я«ЅЯ«БЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Є Я«фЯ»ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ Я«ЄЯ«»Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«▒Я«ЙЯ«░Я»Ї. Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«цЯ»Ї Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я»Ї Я««Я«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»Ђ 60 Я«ЋЯ«┐.Я««Я»ђ. Я«јЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»ЂЯ««Я»Ї, Я«њЯ«░Я»Ђ Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЇЯ«Ъ Я«цЯ«░Я»ЂЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«фЯ»ЄЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«ЕЯ«хЯ»єЯ«ЕЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«хЯ«┐Я«ЪЯ»ѕЯ«»Я«ЙЯ«Ћ Я«ЁЯ««Я»ѕЯ«»Я«ЙЯ«цЯ»Ђ.
Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Ћ, Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«цЯ»Ї Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«еЯ«ЋЯ«░Я»ЂЯ««Я»Ї Я«фЯ»іЯ«░Я»ЂЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«хЯ»ЄЯ«ЋЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЄЯ«ЪЯ«фЯ»ЇЯ«фЯ»єЯ«»Я«░Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«┐Я«ЕЯ»Ї Я«еЯ»ЄЯ«░ Я«хЯ»ђЯ«цЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«хЯ«░Я»ѕЯ«»Я«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ.
vave = Я«фЯ«»Я«Б Я«цЯ»ѓЯ«░Я««Я»Ї / Я«фЯ«»Я«Б Я«еЯ»ЄЯ«░Я««Я»Ї
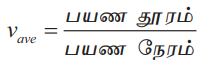
Я«њЯ«░Я»Ђ 10 Я«ЋЯ«┐.Я««Я»ђ Я«фЯ«еЯ»ЇЯ«цЯ«»Я«цЯ»Ї Я«цЯ»ѓЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ Я«ЊЯ«░Я»Ї Я«ЊЯ«ЪЯ»ЇЯ«ЪЯ«фЯ»Ї Я«фЯ«еЯ»ЇЯ«цЯ«» Я«хЯ»ђЯ«░Я«░Я»Ї Я«еЯ«┐Я«▒Я»ѕЯ«хЯ»Ђ Я«џЯ»єЯ«»Я»ЇЯ«» Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«еЯ»ЄЯ«░Я««Я»Ї 1 Я««Я«БЯ«┐ 15 Я«еЯ«┐Я««Я«┐Я«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (1.25 Я««Я«БЯ«┐) Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї.
Я«ЄЯ«еЯ»ЇЯ«ц Я«ЊЯ«ЪЯ»ЇЯ«ЪЯ«фЯ»Ї Я«фЯ«еЯ»ЇЯ«цЯ«»Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЁЯ«хЯ«░Я»ЂЯ«ЪЯ»ѕЯ«» Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐Я«цЯ»Ї Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ««Я»Ї Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«хЯ»ЄЯ«ЋЯ««Я»Ї
vave = 10/1.25 = 8 Я«ЋЯ«┐.Я««Я»ђ. / Я««Я«БЯ«┐ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї.
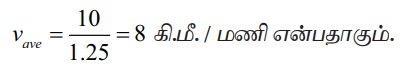
Я«фЯ«еЯ»ЇЯ«цЯ«»Я«цЯ»ЇЯ«цЯ»ѓЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«фЯ«ЙЯ«цЯ«┐Я«цЯ»ЇЯ«цЯ»ѓЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЪЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«цЯ«░Я»ЂЯ«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЊЯ«ЪЯ»ЂЯ«фЯ«хЯ«░Я«┐Я«ЕЯ»Ї Я«хЯ»ЄЯ«ЋЯ««Я»Ї v-Я«»Я«┐Я«ЕЯ»ѕЯ«цЯ»Ї Я«цЯ»ЂЯ«▓Я»ЇЯ«▓Я«┐Я«»Я««Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«Ъ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ»ЂЯ«хЯ»ІЯ««Я»Ї. 0 Я««Я«БЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 0.5 Я««Я«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«еЯ»ЄЯ«░ Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«цЯ»ѓЯ«░Я««Я»Ї 5 Я«ЋЯ«┐.Я««Я»ђ. Я«јЯ«ЕЯ«┐Я«▓Я»Ї, vave = 5/0.5 Я«ЋЯ«┐.Я««Я»ђ/Я««Я«БЯ«┐ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЁЯ«цЯ»Є Я«џЯ««Я«»Я««Я»Ї, Я«ЁЯ«░Я»ѕ Я««Я«БЯ«┐ Я«еЯ»ЄЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЊЯ«ЪЯ»ЂЯ«фЯ«хЯ«░Я«┐Я«ЕЯ»Ї Я«хЯ»ЄЯ«Ћ Я«хЯ»ђЯ«цЯ«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ«ЙЯ«Е Я«ЋЯ«БЯ«еЯ»ЄЯ«░ Я«хЯ»ђЯ«цЯ««Я»Ї v-Я«љ Я«џЯ«┐Я«▒Я«еЯ»ЇЯ«ц Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ«ЙЯ«Ћ Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я«хЯ«┐Я«ЪЯ»ѕЯ«»Я»ѕ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│ Я«ЄЯ«»Я«▓Я«ЙЯ«цЯ»Ђ. Я«цЯ»іЯ«ЪЯ«ЋЯ»ЇЯ«Ћ Я«ЄЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 5.7 Я«ЋЯ«┐.Я««Я»ђ Я«цЯ»ѓЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї 0.6 Я««Я«БЯ«┐Я«»Я«┐Я«▓Я»Ї Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я«ЙЯ«░Я»Ї Я«јЯ«ЕЯ«цЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ««Я«ЙЯ«ЕЯ«┐Я«цЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, 0 Я««Я«БЯ«┐Я«»Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ 0.6 Я««Я«БЯ«┐ Я«хЯ«░Я»ѕЯ«»Я»ЂЯ«│Я»ЇЯ«│ Я«џЯ«░Я«ЙЯ«џЯ«░Я«┐ Я«хЯ»ЄЯ«ЋЯ««Я»Ї vave = 5.7/0.6 РђЊ 0.5 = 7 Я«ЋЯ«┐.Я««Я»ђ./Я««Я«БЯ«┐ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЋЯ«ЪЯ»ѕЯ«џЯ«┐Я«»Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ»єЯ«▒Я«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ v-Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕ Я«џЯ«▒Я»ЇЯ«▒Я»ЄЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«▒Я»ѕЯ«»Я«џЯ»Ї Я«џЯ«░Я«┐Я«»Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ђЯ«ЪЯ«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї. Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«▓ Я«ЄЯ«ЪЯ»ѕЯ«хЯ»єЯ«│Я«┐Я«»Я»ѕ 0.5 Я««Я«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«│Я»Ї РђўЯ«ЋЯ»ЂЯ«▒Я»ѕЯ«фЯ»ЇЯ«фЯ«цЯ«ЕЯ»Ї Я««Я»ѓЯ«▓Я««Я»ЂЯ««Я»Ї' Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЄЯ«▒Я»ЇЯ«ф 5 Я«ЋЯ«┐.Я««Я»ђ. Я«цЯ»ѓЯ«░Я«цЯ»ЇЯ«цЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«њЯ«фЯ»ЇЯ«ф Я«еЯ»ЄЯ«░ Я«ЁЯ«│Я«хЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЊЯ«ЪЯ»ЂЯ«фЯ«хЯ«░Я«┐Я«ЕЯ»Ї Я«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕ Я«ЁЯ«░Я»ѕЯ««Я«БЯ«┐Я«»Я«┐Я«▓Я»Ї Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«џЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ«ЙЯ«Е Я«цЯ»ІЯ«░Я«ЙЯ«» Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ«░ Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї.

Я«цЯ«┐Я«џЯ»ѕЯ«хЯ»ЄЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ«хЯ«цЯ»Ђ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ y = књ(x) Я«јЯ«ЕЯ»ЂЯ««Я»Ї Я«фЯ»іЯ«цЯ»ЂЯ«хЯ«ЙЯ«Е Я«фЯ«ЋЯ»ЂЯ««Я»ЂЯ«▒Я»ѕЯ«џЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ«┐Я«ЕЯ«цЯ»Ђ Я«ЋЯ«БЯ«┐Я«ц Я««Я«ЙЯ«цЯ«┐Я«░Я«┐Я«»Я«┐Я«ЕЯ»Ї Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«ЪЯ»ЂЯ«цЯ«▓Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«ЪЯ»ЂЯ«хЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«ЄЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЁЯ«цЯ«ЕЯ»Ї Я«хЯ«┐Я«│Я»ѕЯ«хЯ«ЙЯ«Ћ Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ІЯ«│Я»ЇЯ«ЋЯ«│Я»ѕЯ«»Я»ЂЯ««Я»Ї, Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«ЙЯ«Ћ Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«ЪЯ»ЂЯ«цЯ«▓Я«┐Я«ЕЯ»Ї Я«фЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ«ЙЯ«»Я»ЇЯ«хЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«»Я»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї.
Я«ЋЯ«▒Я»ЇЯ«▒Я«▓Я«┐Я«ЕЯ»Ї Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї
Я«ЄЯ«фЯ»ЇЯ«фЯ«ЙЯ«ЪЯ«фЯ»ЇЯ«фЯ«ЋЯ»ЂЯ«цЯ«┐ Я«еЯ«┐Я«▒Я»ѕЯ«хЯ»ЂЯ«▒Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я««Я«ЙЯ«БЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ«┐Я«»Я«хЯ»ѕЯ«ЋЯ«│Я«ЙЯ«Ћ
Рђб Я«фЯ«┐Я«ЕЯ»ЇЯ«ЕЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«јЯ«▓Я»ЇЯ«▓Я»ѕЯ«»Я«ЙЯ«Ћ Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»ѕ Я«ЁЯ«▒Я«┐Я«цЯ«▓Я»Ї
Рђб Я«хЯ«ЪЯ«┐Я«хЯ«┐Я«»Я«▓Я»Ї Я«░Я»ђЯ«цЯ«┐Я«»Я«ЙЯ«Ћ Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЂЯ«цЯ«▓Я»Ї
Рђб Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЁЯ«│Я«хЯ»ђЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▓Я«ЙЯ«Ћ Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ«цЯ«▓Я»Ї
Рђб Я«хЯ«│Я»ѕЯ«хЯ«░Я»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»ђЯ«цЯ«ЙЯ«Е Я«цЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ІЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ«ЙЯ«»Я»ЇЯ«хЯ«ЙЯ«ЋЯ«хЯ»ЂЯ««Я»Ї/Я««Я«ЙЯ«▒Я»ЂЯ«хЯ»ђЯ«цЯ««Я»Ї Я«єЯ«ЋЯ«хЯ»ЂЯ««Я»Ї Я«хЯ«ЋЯ»ѕЯ«»Я»ђЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ»ѕ Я«ЅЯ«БЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ«цЯ«▓Я»Ї
Рђб Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«ЪЯ»ЂЯ«цЯ«▓Я«┐Я«ЕЯ»Ї Я«фЯ«▓Я»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я»ѕ Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ«цЯ«▓Я»Ї
Рђб Я«ЁЯ«ЕЯ»ЇЯ«▒Я«ЙЯ«Ъ Я«еЯ«┐Я«ЋЯ«┤Я»ЇЯ«хЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«хЯ«┐Я«»Я«ЙЯ«Ћ Я«хЯ«ЋЯ»ѕ Я«еЯ»ЂЯ«БЯ»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї. Я«єЯ«ЋЯ«┐Я«»Я«хЯ»ѕ Я«јЯ«цЯ«┐Я«░Я»ЇЯ«фЯ«ЙЯ«░Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е.