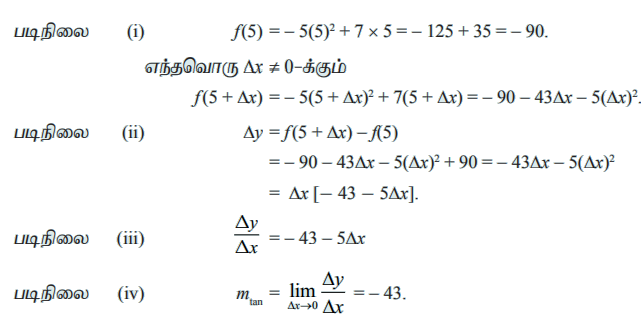தொடுகோடுக் கணக்கு (The tangent line problem) - வகையிடுதலின் கருத்தாக்கம் (The concept of derivative)

தொடுகோடுக் கணக்கு (The tangent line problem)

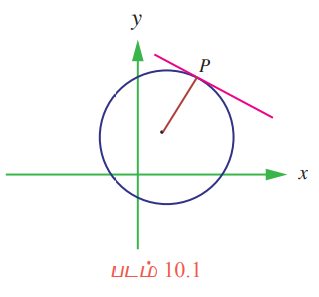
ஒரு வளைவரையில் குறிப்பிட்ட ஒரு புள்ளியில் ஒரு நேர்க்கோடு தொடுகோடாக அமைகின்றது என்பதன் பொருள் என்ன? ஒரு வட்டத்தில் ‘P' எனும் புள்ளியின் மீது தொட்டுச் செல்லும் தொடுகோடு என்பது படம் 10.1-ல் கண்டுள்ளவாறு 'P' எனும் புள்ளியைச் சந்திக்கும் ஆரக்கோட்டிற்குச் செங்குத்துக் கோடாக (radial line) அமையும்.

ஆனால் பொதுவான வளைவரையாக இருந்தால் தொடுகோட்டைக் கண்டறிவது மிகக் கடினமான செயலாகும். எடுத்துக்காட்டாக கீழ்க்காணும் 10.2-லிருந்து 10.4 வரையிலான படங்களில் உள்ளவற்றிற்குத் தொடுகோடுகளை எவ்வாறு வரையறுக்க இயலும்?

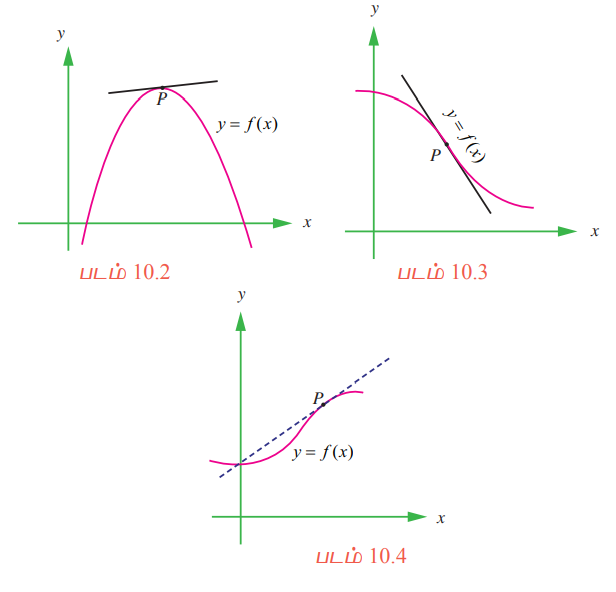
‘P’ எனும் புள்ளியில் வளைவரையை வெட்டிச் செல்லாமல் தொட்டுச் செல்லும் கோடுதான் தொடுகோடாக அமையும் எனக் கூற முனையலாம். இந்த வரையறை படம் 10.2-ல் உள்ளது போன்ற வளைவரைக்குப் பொருந்தும், ஆனால் 10.3-ல் உள்ள வளைவரைக்குப் பொருந்தாது, அல்லது ஒரு வளைவரைக்கு ஒரு கோடு தொடுகோடாக அமைய வேண்டுமெனில், கோடும் வளைவரையும் ஒரே ஒரு புள்ளியில் தொட்டுச் செல்லவோ அல்லது சந்திக்கவோ வேண்டும். ஆனால் இந்த வரையறை வட்டத்திற்குப் பொருந்தக் கூடும். ஆனால் படம் 10.4-ல் உள்ளது போன்ற பொதுவான வளைவரைகளுக்கு இந்த வரையறை பொருந்தாது.

அடிப்படையில் ‘P' எனும் புள்ளியில் உள்ள தொடுகோட்டைக் கண்டறிய முயல்வது ‘P’ எனும் புள்ளியில் தொடுகோட்டின் சாய்வினைக் கண்டறிவதாக மாறுகிறது.

இச்சாய்வினை, தொடுவரைப்புள்ளி (point of tangency) மற்றும் வளைவரையின் மீதான மற்றொரு புள்ளி வழியாகச் செல்லும் வெட்டுக் கோட்டின் சாய்வுக்குத் தோராயமாகப் படம் 10.5ல் காண்பதுபோல் காணலாம்.

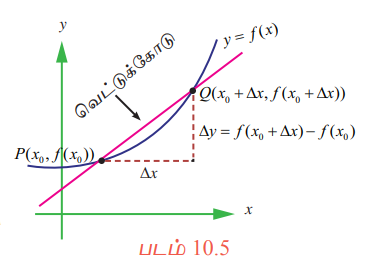
தொடுவரைப்புள்ளியாக P(x0, ƒ(x0)) எனவும் இரண்டாவது புள்ளியாக Q(x0 + ∆x, ƒ(x0 + ∆ x)) எனவும் கருதுவோம்.

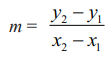 எனும் சாய்வு விதியில் பிரதியிடுவதன் மூலம் இரு புள்ளிகள் வழியாகச் செல்லும்  வெட்டுக் கோட்டின் சாய்வைப் பெற இயலும்.

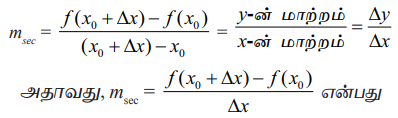
வெட்டுக்கோட்டின் சாய்வாக அமையும்.

இந்தச் சமன்பாட்டின் வலப்பக்கம் இருப்பது வேறுபாட்டுப் பின்னம் (Difference quotient) ஆகும்.

பகுதி ∆ x என்பது x-ன் மாற்றம் (x-ன் அதிகரிப்பு) மற்றும் தொகுதி ∆y = ƒ(x0 + ∆ x) - ƒ(x0) என்பது y-ன் மாற்றம் ஆகும்.

தொடுவரைப்புள்ளிக்கு மிக அருகே புள்ளிகளைத் தேர்ந்தெடுப்பதன் மூலம் தொடுகோட்டின் சாய்விற்கான சிறந்த தோராய மதிப்பினைப் பெற இயலும் என்பதே இம்முறையின் சிறப்பம்சம் ஆகும்.

விளக்க எடுத்துக்காட்டு 10.1

ƒ(x) = x2 எனும் வளைவரைக்கு (1,1) என்ற புள்ளியில் தொடுகோட்டின் சாய்வினைக் கண்டறிவோம்.

முதலில் ∆x = 0.1 எனக் கருதுவோம். (1, 1) மற்றும் (1.1, (1.1)2) புள்ளிகள் வழியாகச் செல்லும் வெட்டுக்கோட்டின் சாய்வினைக் கண்டறிவோம்.

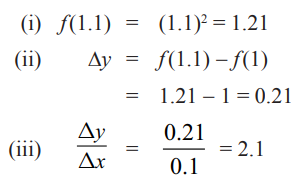
1-க்கு வலப்பக்கமும் இடப்பக்கமும் அமையும் அடுத்தடுத்த மதிப்புகளைக் கீழ்க்காணும் வகையில் அட்டவணைப்படுத்துவோம்.

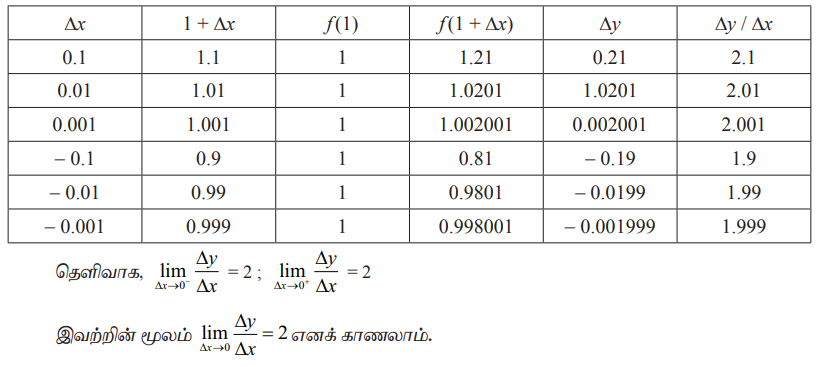
எனவே, y = x2 எனும் வளைவரையின் தொடுகோட்டின் சாய்வு (1, 1) எனும் புள்ளியில் mtan = 2 என அமையும்.

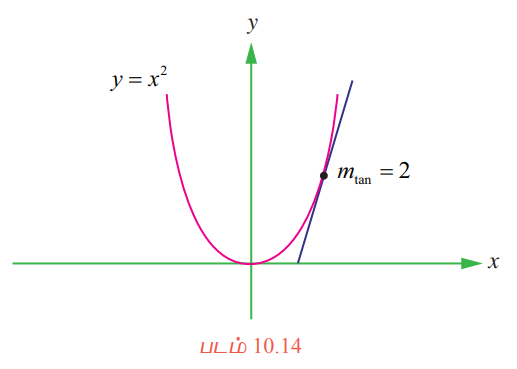
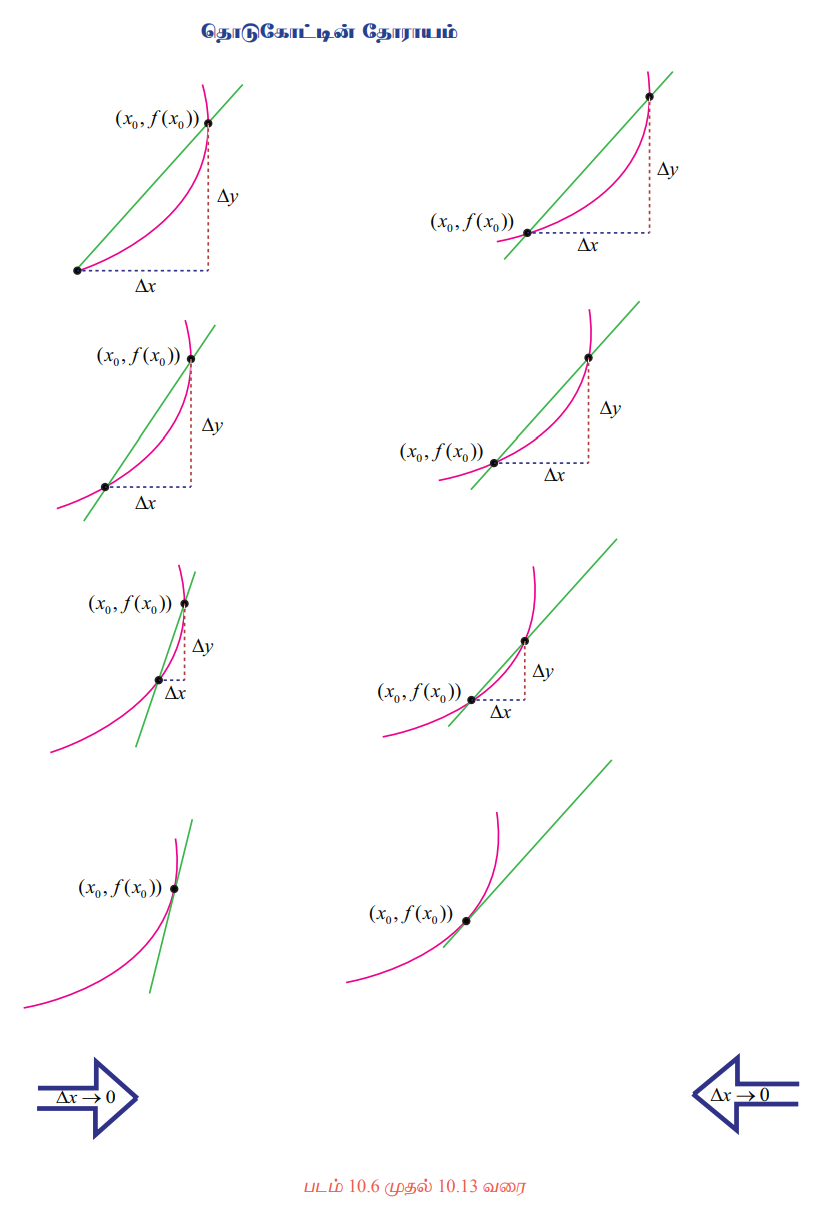
படங்கள் 10.6 முதல் 10.13, விளக்க எடுத்துக்காட்டு 10.1 மற்றும் நமது உள்ளுணர்வின் வாயிலாக, “P எனும் புள்ளியில் y = ƒ(x) எனும் வளைவரையின் ‘L’' எனும் தொடுகோடு, Q → P (∆x → 0) எனுமாறு P மற்றும் Q-ன் வழியாகச் செல்லும் வெட்டுக்கோடு PQ -ன் எல்லை என எடுத்துரைக்க இயலும்'. மேலும் L-ன் சாய்வு mtan என்பது ∆x → 0 எனும்போது msec -ன் எல்லை மதிப்பாக அமையும். இதனையே பின்வருமாறு தொகுத்துக் கூறலாம்:

வரையறை 10.1 (சாய்வு m உள்ள தொடுகோடு) (Tangent line with slope m)

x0 என்ற புள்ளி அமைந்துள்ள திறந்த இடைவெளியில் ƒ என்ற சார்பினை வரையறுப்போம்.

மேலும், 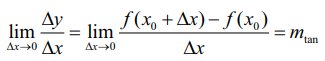 கிடைக்கப்பெற்றால், m எனும் சாய்வுடன் (x0, ƒ(x0)) புள்ளி வழியாகச் செல்லும் கோடு, (x0, ƒ(x0)) எனும் புள்ளியில் ƒ எனும் வளைவரையின் தொடுகோடாக அமையும்.

(x0, ƒ(x0)) என்ற புள்ளியில் வரையப்பட்ட தொடுகோட்டின் சாய்வு, அப்புள்ளியில் வளைவரையின் சாய்வு எனவும் அழைக்கப்படுகிறது,

வரையறையின் மூலம் ஒரு வளைவரை (x0, ƒ(x0)) என்ற புள்ளியில் ஒரு தொடுகோட்டினைத் தருமாயின் அது தனித்ததாக இருக்கும். ஏனெனில் கொடுக்கப்பட்ட ஒரு புள்ளி மற்றும் சாய்வு வழியாக ஒரே ஒரு கோட்டினையே வரைய இயலும்.

வளைவரையின் சாய்வைக் காண்பதற்கான நிபந்தனைகளை 4 படி நிலைகளாக எழுதலாம்.

(i) x0 மற்றும் x0 + ∆x என்ற புள்ளிகளில் ƒ-ன் மதிப்புகளைக் காண்க. அதாவது, ƒ(x0) மற்றும் ƒ(x0 + ∆x)  ஆகியவற்றைக் காண்க.

(ii) ∆y கணக்கிடுக: அதாவது ∆y = ƒ(x0 + ∆x) - ƒ(x0) - ஐ காண்க.

(iii) ∆y- ஐ ∆x ≠ 0 ஆல் வகுக்க : அதாவது, 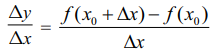  -ஐ காண்க.

(iv) ∆x  → 0 (∆x ≠ 0) எனும்போது: ∆y/∆x  -ன் எல்லையைக் காண்க. அதாவது,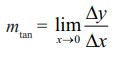

விளக்க எடுத்துக்காட்டு10.1-ல் உள்ள வளைவரையின் சாய்வினைக் காண்பதை எளிமைப்படுத்த வரையறைகள் பயன்படுவதைக் காணலாம்.

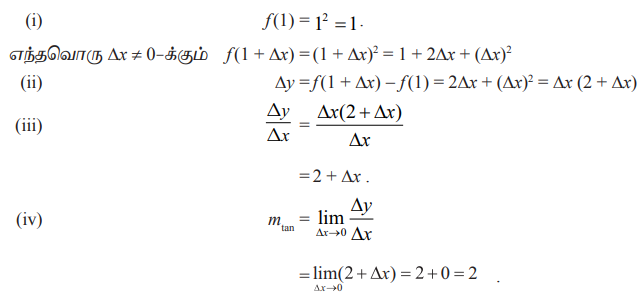
எடுத்துக்காட்டு 10.1

ƒ(x) = 7x + 5 எனும் வளைவரைக்கு (x0,ƒ(x0)) எனும் புள்ளியில் தொடுகோட்டின் சாய்வினைக் காண்க.

தீர்வு

படிநிலை (i) ƒ(x0) = 7x0 + 5

எந்தவொரு ∆x ≠ 0 –க்கும்,

ƒ(x0 + ∆x) = 7(x0 + ∆x) + 5

= 7x0 + 7∆x + 5

படிநிலை (ii) ∆x = ƒ(x0 + ∆x)- f(x0)

= (7x0 + 7∆x + 5) – (7x0 + 5)

= 7∆x

படிநிலை (iii) ∆y/∆x = 7

எனவே, ƒ(x) = 7 x + 5 எனும் வளைவரையில் உள்ள எந்தவொரு புள்ளிக்கும்,

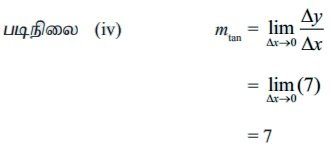
ஒரு நேரிய வளைவரைக்கு, ∆y / ∆x என்பது x0 மற்றும் ஏற்ற மதிப்பான ∆x ஆகியவற்றை சாராமல் ஒரு மாறிலியாக இருக்கும் என்பதனைக் கவனத்தில் கொள்ளவும்.

எடுத்துக்காட்டு 10.2

ƒ(x) = -5x2 + 7x எனும் வளைவரைக்கு (5,ƒ(5)) என்ற புள்ளியில் தொடுகோட்டின் சாய்வினைக் காண்க.

தீர்வு