11 வது கணக்கு : அலகு 10 : வகை நுண்கணிதம் வகைமை மற்றும் வகையிடல் முறைகள் DIFFERENTIABILITY AND METHODS OF DIFFERENTIATION
வகையிடல் விதிகள் (Differentiation Rules)
வகையிடல் விதிகள் (Differentiation Rules)
I எனும் திறந்த இடைவெளியில் மெய்மாறிக்கு வரையறுக்கப்படும் மெய் மதிப்புடைய சார்பு ƒ மற்றும் y = ƒ(x) என்பது x -ன் வகைமைச் சார்பு எனில், 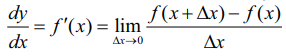 ஆகும்.
ஆகும்.
பொதுவாக முதல் கொள்கையைப் பயன்படுத்தி வகையிடல் காணும் முறை பல இடங்களில் கடினமாகவும் நேர விரயத்தை ஏற்படுத்துவதாகவும் உள்ளது. ஆனால் அனைத்து அடிப்படையான மூலச்சார்புகளுக்கான வகையிடலை அறிந்து, மேலும் சார்புகளின் கணிதச் செயல்பாடுகளைக் கொண்டு வகையிடல் முறையையும், சார்பின் மீதான சார்புகள் முறையையும் அறிந்திருந்தால் ஒவ்வொரு முறையும் எல்லைச் செயலைப் பயன்படுத்தாமல் அனைத்திற்கும் வகையிடல் கண்டறிய இயலும். எனவே வகையிடல் மீதான செயல்பாடுகளை நேரடியாகவே செய்து விடலாம். இப்போது சார்புகளின் கூடுதல், பெருக்கல் மற்றும் வகுத்தலுக்கான வகையிடல் விதிகளின் மீது கவனத்தைச் செலுத்துவோம்.
தேற்றம் 10.2
இரண்டு (அல்லது இரண்டிற்கு மேற்பட்ட) வகைமையான சார்புகளின் கூடுதலின் வகையிடலும் அச்சார்புகளின் தனித்தனியான வகையிடலின் கூடுதலும் சமமாக இருக்கும். அதாவது u மற்றும் v என்பவை இரு வகையிடத்தக்க சார்புகள் எனில் 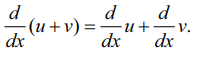
நிரூபணம்
I ⊆ ℝ எனும் திறந்த இடைவெளியில் வரையறுக்கப்பட்ட வகைமையான இரு மெய் மதிப்புடைய சார்புகள் u மற்றும் v என்க. y = u + v எனில் y = ƒ (x) என்பது I-ல் வரையறுக்கப்பட்ட சார்பாகும். அனுமானத்தின்படி,

இதனை முடிவுறு எண்ணிக்கையிலான வகைமையான u1,u2,...,un ஆகிய சார்புகளுக்கும் விரிவுபடுத்தலாம். (u1 + u2 + ...+ un)' = u1’ + u2 ’ + …… un’
தேற்றம் 10.3
u மற்றும் v என்பவை இரு வகையிடத்தக்க சார்புகள் எனில் 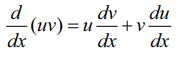
நிரூபணம்
u மற்றும் v என்பன கொடுக்கப்பட்ட இரு வகைமையான சார்புகள் ஆதலால்,

மேலும் இதனை முடிவுறு எண்ணிக்கையிலான வகைமையான u1,u2,...,un சார்புகளுக்கு நீட்டித்து, கணிதத் தொகுத்தறிதல் மூலம் கீழ்வருமாறு பெறலாம் :
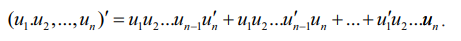
தேற்றம் 10.4 (வகுத்தல் விதி) (Quotient Rule)
u மற்றும் v வகையான இரு சார்புகள், v(x) ≠ 0. எனில் 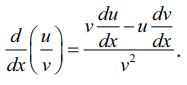
நிரூபணம்

தேற்றம் 10.5 (இணைப்பு விதி / சார்புகளின் சேர்ப்பின் விதி / சார்பின் சார்பு விதி) (Chain Rule / Composite Function Rule or Function of a Function Rule)
y = ƒ(u) என்பது u-ன் சார்பாகவும் மேலும் u = g(x) என்பது x -ன் சார்பாகவும் இருப்பின்
y = ƒ (g(x)) = (fog)( x) . இப்போது 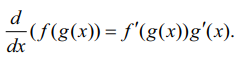
நிரூபணம்
y = ƒ (g(x)) = (fog)( x)
மேற்கண்ட சார்பில் u = g(x) என்பது உட்சார்பு எனவும், ƒ என்பது வெளிப்புறச் சார்பு எனவும் அழைக்கப்படுகிறது.
முத்தாய்ப்பாக y என்பது x -ன் சார்பாகும்.
இப்போது Δu = g(x+Δx) - g(x)
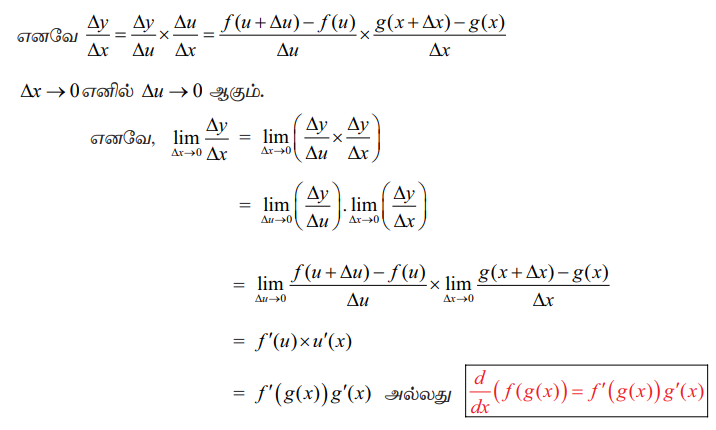
எனவே y = ƒ = (g(x)) எனும் சார்பினை வகையிட g(x) = u என்பதைப் பொறுத்து வெளிப்புறச்சார்பு ƒ-ன் வகையிடலைச் சாரா மாறி x -ஐ பொறுத்து உட்புறச் சார்பின் வகையிடலுடன் பெருக்க வேண்டும். இங்கு u என்பது இடைப்பட்ட மாறி என அழைக்கப்படுகிறது.
தேற்றம் 10.6
ƒ(x) என்ற சார்பு வகைமையானதாகவும், y = kf(x), k ≠ 0 எனில் d/dx (kf(x)) = k(d/dx) f(x) 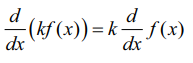
நிரூபணம்
ƒ(x) என்பது வகைமையான சார்பு என்க. y = kf(x), k ≠ 0 என்க.

1. அடிப்படைச் சார்புகளின் வகைக்கெழு (Derivatives of basic elementary functions)
அனைத்து அடிப்படைச் சார்புகளின் வகையிடல் முறையை காண்போம். முதலில் மாறிலிச் சார்பினை எடுத்துக் கொள்வோம்.
(1) மாறிலிச் சார்பின் வகையிடல் பூஜ்ஜியமாகும்
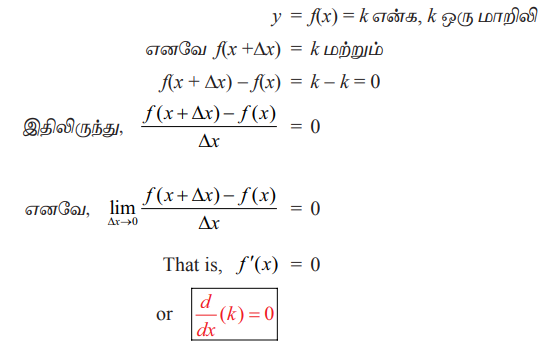
(2) y= x" எனும் அடுக்குச் சார்பு, n > 0 என்பது ஒரு முழு எண்
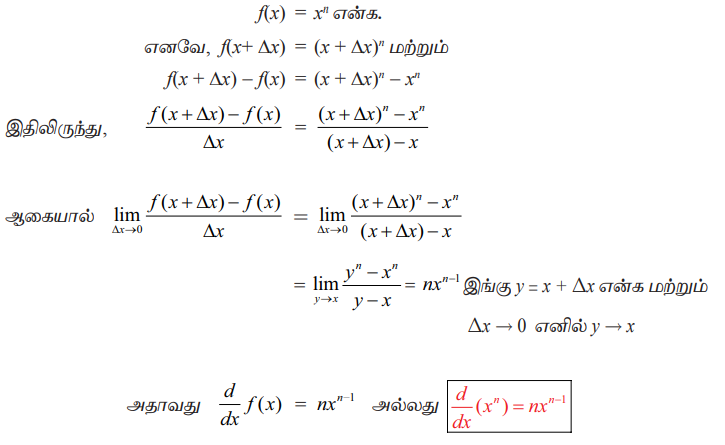
கிளைத்தேற்றம் 10.1
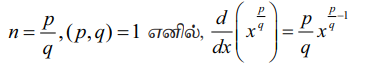
கிளைத்தேற்றம் 10.2
a என்பது ஏதேனும் ஒரு மெய்யெண் எனில், d/dx(xa) = axa-1
சில உதாரணங்கள்


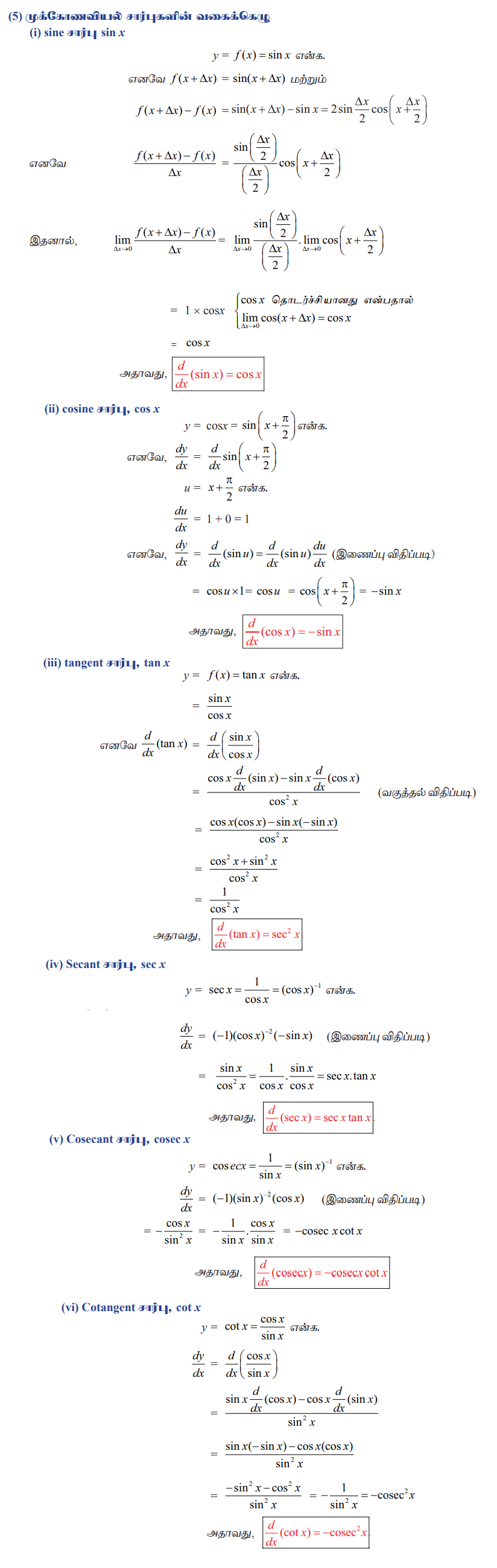


2. சார்பின் சார்பினது வகைக்கெழு (இணைப்பு விதி) எடுத்துக்காட்டுகள்

