வகையிடுதலின் கருத்தாக்கம் (The concept of derivative)

வகையிடுதலின் கருத்தாக்கம் (The concept of derivative)

பதினேழாம் நூற்றாண்டில் கணிதவியலாளர்கள் தீர்வு காண முயன்ற நான்கு முக்கியமான கணக்குகளிலிருந்து வகைநுண் கணிதம் தோன்றி வளர்ச்சி பெற்றது. அவை

(1) தொடுகோடுக் கணக்கு

(2) திசைவேகம் மற்றும் முடுக்கக் கணக்கு

(3) சிறுமம் மற்றும் பெருமக் கணக்கு

(4) பரப்பளவுக் கணக்கு.

முதலிரண்டு கணக்குகளைப் பற்றி இப்பாடப்பகுதியில் காண்போம். ஏனைய இரண்டினைப் பின்னர் வரும் பாடப்பகுதியில் காணலாம்.

1. தொடுகோடுக் கணக்கு (The tangent line problem)

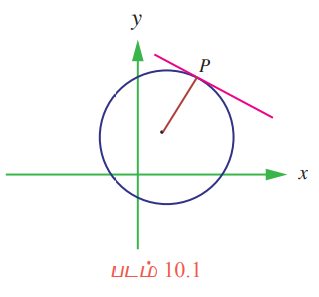
ஒரு வளைவரையில் குறிப்பிட்ட ஒரு புள்ளியில் ஒரு நேர்க்கோடு தொடுகோடாக அமைகின்றது என்பதன் பொருள் என்ன? ஒரு வட்டத்தில் ‘P' எனும் புள்ளியின் மீது தொட்டுச் செல்லும் தொடுகோடு என்பது படம் 10.1-ல் கண்டுள்ளவாறு 'P' எனும் புள்ளியைச் சந்திக்கும் ஆரக்கோட்டிற்குச் செங்குத்துக் கோடாக (radial line) அமையும்.

ஆனால் பொதுவான வளைவரையாக இருந்தால் தொடுகோட்டைக் கண்டறிவது மிகக் கடினமான செயலாகும். எடுத்துக்காட்டாக கீழ்க்காணும் 10.2-லிருந்து 10.4 வரையிலான படங்களில் உள்ளவற்றிற்குத் தொடுகோடுகளை எவ்வாறு வரையறுக்க இயலும்?

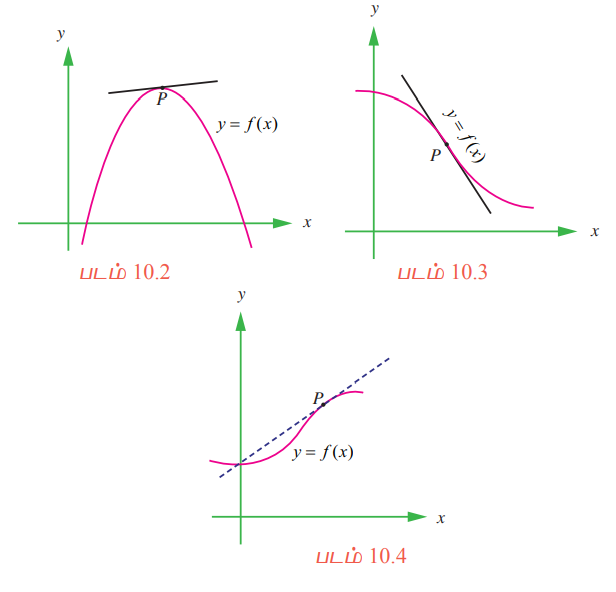
‘P’ எனும் புள்ளியில் வளைவரையை வெட்டிச் செல்லாமல் தொட்டுச் செல்லும் கோடுதான் தொடுகோடாக அமையும் எனக் கூற முனையலாம். இந்த வரையறை படம் 10.2-ல் உள்ளது போன்ற வளைவரைக்குப் பொருந்தும், ஆனால் 10.3-ல் உள்ள வளைவரைக்குப் பொருந்தாது, அல்லது ஒரு வளைவரைக்கு ஒரு கோடு தொடுகோடாக அமைய வேண்டுமெனில், கோடும் வளைவரையும் ஒரே ஒரு புள்ளியில் தொட்டுச் செல்லவோ அல்லது சந்திக்கவோ வேண்டும். ஆனால் இந்த வரையறை வட்டத்திற்குப் பொருந்தக் கூடும். ஆனால் படம் 10.4-ல் உள்ளது போன்ற பொதுவான வளைவரைகளுக்கு இந்த வரையறை பொருந்தாது.

அடிப்படையில் ‘P' எனும் புள்ளியில் உள்ள தொடுகோட்டைக் கண்டறிய முயல்வது ‘P’ எனும் புள்ளியில் தொடுகோட்டின் சாய்வினைக் கண்டறிவதாக மாறுகிறது.

இச்சாய்வினை, தொடுவரைப்புள்ளி (point of tangency) மற்றும் வளைவரையின் மீதான மற்றொரு புள்ளி வழியாகச் செல்லும் வெட்டுக் கோட்டின் சாய்வுக்குத் தோராயமாகப் படம் 10.5ல் காண்பதுபோல் காணலாம்.

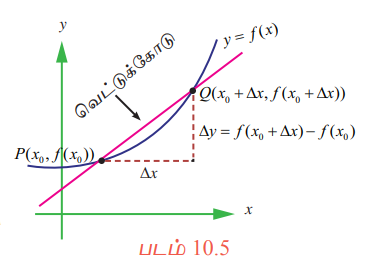
தொடுவரைப்புள்ளியாக P(x0, ƒ(x0)) எனவும் இரண்டாவது புள்ளியாக Q(x0 + ∆x, ƒ(x0 + ∆ x)) எனவும் கருதுவோம்.

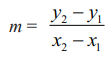 எனும் சாய்வு விதியில் பிரதியிடுவதன் மூலம் இரு புள்ளிகள் வழியாகச் செல்லும்  வெட்டுக் கோட்டின் சாய்வைப் பெற இயலும்.

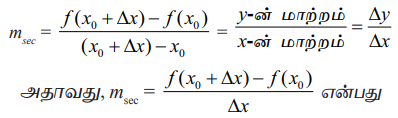
வெட்டுக்கோட்டின் சாய்வாக அமையும்.

இந்தச் சமன்பாட்டின் வலப்பக்கம் இருப்பது வேறுபாட்டுப் பின்னம் (Difference quotient) ஆகும்.

பகுதி ∆ x என்பது x-ன் மாற்றம் (x-ன் அதிகரிப்பு) மற்றும் தொகுதி ∆y = ƒ(x0 + ∆ x) - ƒ(x0) என்பது y-ன் மாற்றம் ஆகும்.

தொடுவரைப்புள்ளிக்கு மிக அருகே புள்ளிகளைத் தேர்ந்தெடுப்பதன் மூலம் தொடுகோட்டின் சாய்விற்கான சிறந்த தோராய மதிப்பினைப் பெற இயலும் என்பதே இம்முறையின் சிறப்பம்சம் ஆகும்.

விளக்க எடுத்துக்காட்டு 10.1

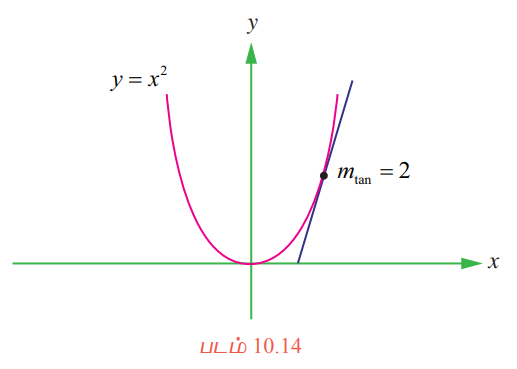
ƒ(x) = x2 எனும் வளைவரைக்கு (1,1) என்ற புள்ளியில் தொடுகோட்டின் சாய்வினைக் கண்டறிவோம்.

முதலில் ∆x = 0.1 எனக் கருதுவோம். (1, 1) மற்றும் (1.1, (1.1)2) புள்ளிகள் வழியாகச் செல்லும் வெட்டுக்கோட்டின் சாய்வினைக் கண்டறிவோம்.

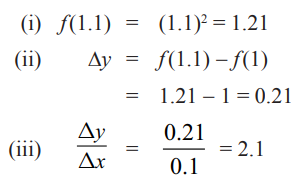
1-க்கு வலப்பக்கமும் இடப்பக்கமும் அமையும் அடுத்தடுத்த மதிப்புகளைக் கீழ்க்காணும் வகையில் அட்டவணைப்படுத்துவோம்.

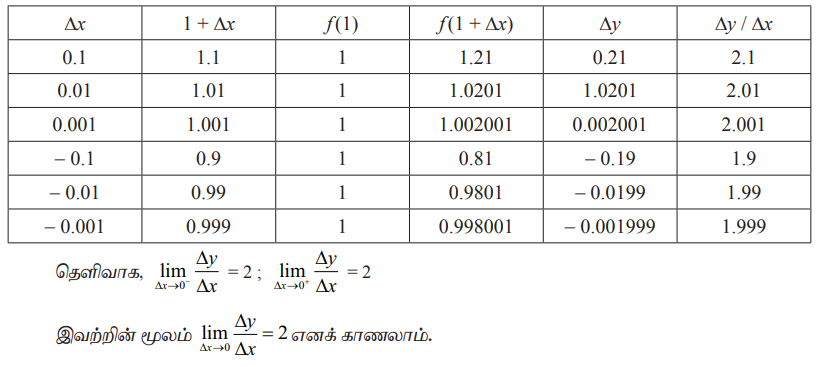
எனவே, y = x2 எனும் வளைவரையின் தொடுகோட்டின் சாய்வு (1, 1) எனும் புள்ளியில் mtan = 2 என அமையும்.

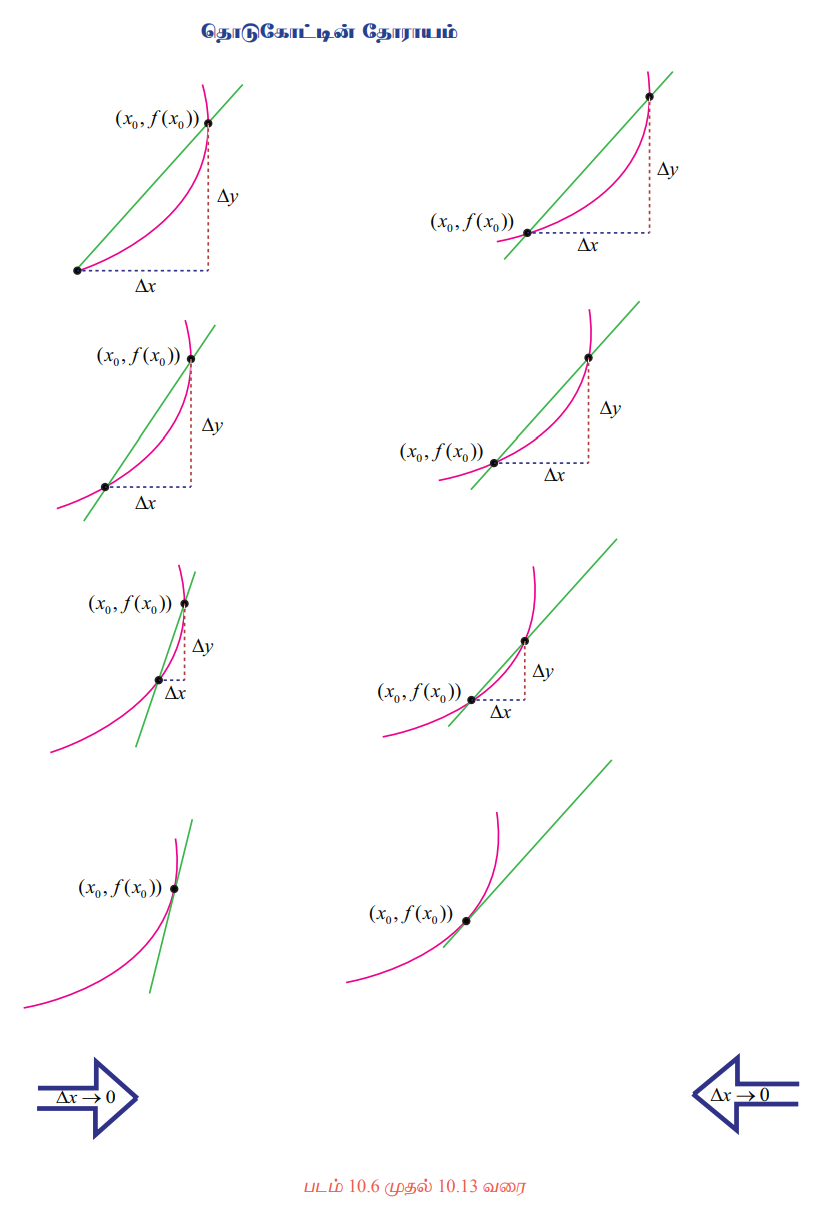
படங்கள் 10.6 முதல் 10.13, விளக்க எடுத்துக்காட்டு 10.1 மற்றும் நமது உள்ளுணர்வின் வாயிலாக, “P எனும் புள்ளியில் y = ƒ(x) எனும் வளைவரையின் ‘L’' எனும் தொடுகோடு, Q → P (∆x → 0) எனுமாறு P மற்றும் Q-ன் வழியாகச் செல்லும் வெட்டுக்கோடு PQ -ன் எல்லை என எடுத்துரைக்க இயலும்'. மேலும் L-ன் சாய்வு mtan என்பது ∆x → 0 எனும்போது msec -ன் எல்லை மதிப்பாக அமையும். இதனையே பின்வருமாறு தொகுத்துக் கூறலாம்:

வரையறை 10.1 (சாய்வு m உள்ள தொடுகோடு) (Tangent line with slope m)

x0 என்ற புள்ளி அமைந்துள்ள திறந்த இடைவெளியில் ƒ என்ற சார்பினை வரையறுப்போம்.

மேலும், 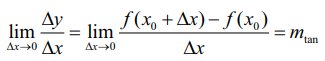 கிடைக்கப்பெற்றால், m எனும் சாய்வுடன் (x0, ƒ(x0)) புள்ளி வழியாகச் செல்லும் கோடு, (x0, ƒ(x0)) எனும் புள்ளியில் ƒ எனும் வளைவரையின் தொடுகோடாக அமையும்.

(x0, ƒ(x0)) என்ற புள்ளியில் வரையப்பட்ட தொடுகோட்டின் சாய்வு, அப்புள்ளியில் வளைவரையின் சாய்வு எனவும் அழைக்கப்படுகிறது,

வரையறையின் மூலம் ஒரு வளைவரை (x0, ƒ(x0)) என்ற புள்ளியில் ஒரு தொடுகோட்டினைத் தருமாயின் அது தனித்ததாக இருக்கும். ஏனெனில் கொடுக்கப்பட்ட ஒரு புள்ளி மற்றும் சாய்வு வழியாக ஒரே ஒரு கோட்டினையே வரைய இயலும்.

வளைவரையின் சாய்வைக் காண்பதற்கான நிபந்தனைகளை 4 படி நிலைகளாக எழுதலாம்.

(i) x0 மற்றும் x0 + ∆x என்ற புள்ளிகளில் ƒ-ன் மதிப்புகளைக் காண்க. அதாவது, ƒ(x0) மற்றும் ƒ(x0 + ∆x)  ஆகியவற்றைக் காண்க.

(ii) ∆y கணக்கிடுக: அதாவது ∆y = ƒ(x0 + ∆x) - ƒ(x0) - ஐ காண்க.

(iii) ∆y- ஐ ∆x ≠ 0 ஆல் வகுக்க : அதாவது, 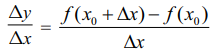  -ஐ காண்க.

(iv) ∆x  → 0 (∆x ≠ 0) எனும்போது: ∆y/∆x  -ன் எல்லையைக் காண்க. அதாவது,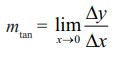

விளக்க எடுத்துக்காட்டு10.1-ல் உள்ள வளைவரையின் சாய்வினைக் காண்பதை எளிமைப்படுத்த வரையறைகள் பயன்படுவதைக் காணலாம்.

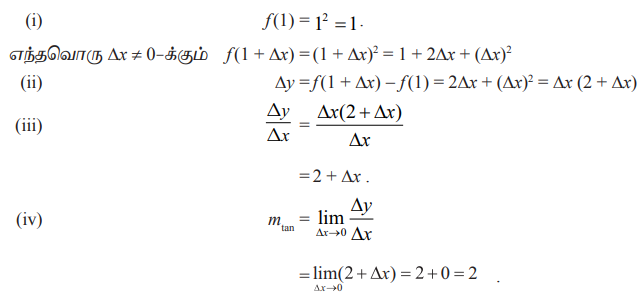
எடுத்துக்காட்டு 10.1

ƒ(x) = 7x + 5 எனும் வளைவரைக்கு (x0,ƒ(x0)) எனும் புள்ளியில் தொடுகோட்டின் சாய்வினைக் காண்க.

தீர்வு

படிநிலை (i) ƒ(x0) = 7x0 + 5

எந்தவொரு ∆x ≠ 0 –க்கும்,

ƒ(x0 + ∆x) = 7(x0 + ∆x) + 5

= 7x0 + 7∆x + 5

படிநிலை (ii) ∆x = ƒ(x0 + ∆x)- f(x0)

= (7x0 + 7∆x + 5) – (7x0 + 5)

= 7∆x

படிநிலை (iii) ∆y/∆x = 7

எனவே, ƒ(x) = 7 x + 5 எனும் வளைவரையில் உள்ள எந்தவொரு புள்ளிக்கும்,

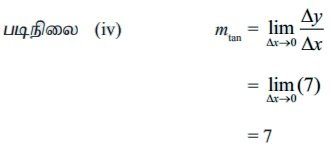
ஒரு நேரிய வளைவரைக்கு, ∆y / ∆x என்பது x0 மற்றும் ஏற்ற மதிப்பான ∆x ஆகியவற்றை சாராமல் ஒரு மாறிலியாக இருக்கும் என்பதனைக் கவனத்தில் கொள்ளவும்.

எடுத்துக்காட்டு 10.2

ƒ(x) = -5x2 + 7x எனும் வளைவரைக்கு (5,ƒ(5)) என்ற புள்ளியில் தொடுகோட்டின் சாய்வினைக் காண்க.

தீர்வு

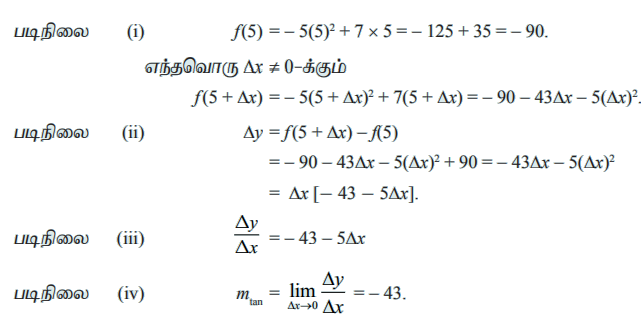
2. நேர்க்கோட்டியக்கத்தில் திசைவேகம் (Velocity of Rectilinear motion)

ஆதியிலிருந்து ‘t’ நேரத்தில் ஒரு பொருளின் நகர்வு (இயக்கப்பட்ட தூரம்) s என்க. s=ƒ(t) எனும் இயக்கச் சமன்பாட்டின்படி அப்பொருள் நேர்க்கோட்டில் நகர்வதாகக்கொள்வோம். இங்கு இயக்கத்தை விவரிக்கும் ‘ƒ' எனும் சார்புப் பொருளின் 'நிலைச்சார்பு' (position function) என அழைக்கப்படுகிறது. t = t0-லிருந்து t = t0 + ∆t எனும் நேர இடைவெளியில் நிலை மாற்றம் ƒ(t0 + ∆t) - ƒs(t0) ஆகும். இந்த நேர இடைவெளியில் சராசரி திசைவேகம்

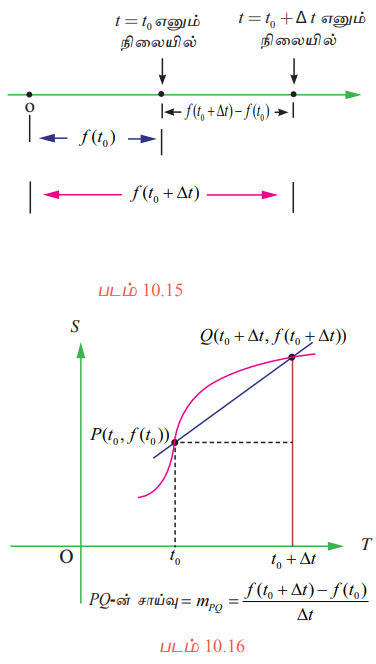
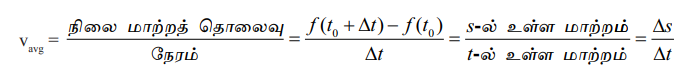
இது படம் 10.16-ல் உள்ளபடி PQ எனும் வெட்டுக்கோட்டின் சாய்வு ஆகும்.

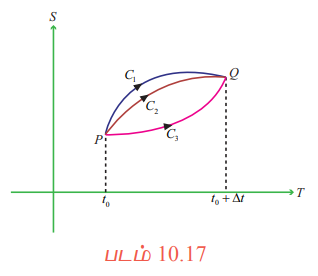
நேர இடைவெளி ∆t -ல் (t0 -லிருந்து t0 + ∆t வரை) தூரத்தை நிறைவு செய்தல் (செல்லும் தூரம்) ஒன்றாக இருந்தாலும் இயக்கம் பல வகையாக அமையலாம். இது ஒரு தளத்திலுள்ள P மற்றும் Q புள்ளிகளுக்கிடையே முற்றிலும் வெவ்வேறான C1, C2, C3 ...... வளைவரைகள் மூலம் விளக்கப்பட்டுள்ளது. (படம் 10.17) இந்த வரைபடத்தில் உள்ள வளைவரைகள் கொடுக்கப்பட்ட நேர இடைவெளிகளில், அனைத்து இயக்கங்களுக்கும் ∆s / ∆t எனும் ஒரே சராசரித் திசைவேகம் கொண்டதாகவும் ஆனால், முற்றிலும் வெவ்வேறான இயக்கங்களாகவும் அமைகின்றது.

[t0, t0 + ∆t] எனும் குறுகிய மற்றும் மேலும் தொடர்ந்து குறுகிய நேர இடைவெளிகளில் சராசரித் திசைவேகங்களை இப்போது கணக்கிடுவோம். வேறு விதமாகக் கூறுவதென்றால், ∆t என்பது 0-வை அணுகுவதாக கொள்வோம். இப்போது t = t0 என்ற நேரத்தில் திசைவேகத்தினை v(t0) (கணநேர திசைவேகம்) சராசரித் திசைவேகங்களின் எல்லையாகக் காணலாம்.

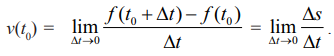
இதிலிருந்து t = t0 என்ற நேரத்தில் திசைவேகம் என்பதும் P என்ற புள்ளியில் தொடுகோட்டின் சாய்வும் சமமாக இருக்கிறது என்பது தெளிவாகிறது.

விளக்க எடுத்துக்காட்டு 10.2

வெற்றிட வெளியில் தடையின்றி விழும் ஒரு பொருள் கடந்த தூரம் s என்க. அதற்கு எடுத்துக்கொள்ளும் நேரம் t என்க. இவை இரண்டும் மாறிகளாகவும் ஒன்றையொன்று சார்ந்ததாகவும் இருக்கும். தடையற்று விழும் விதிப்படி மேற்கண்ட சார்ந்த தன்மையைக் கீழ்க்காணுமாறு விவரிக்கலாம்:

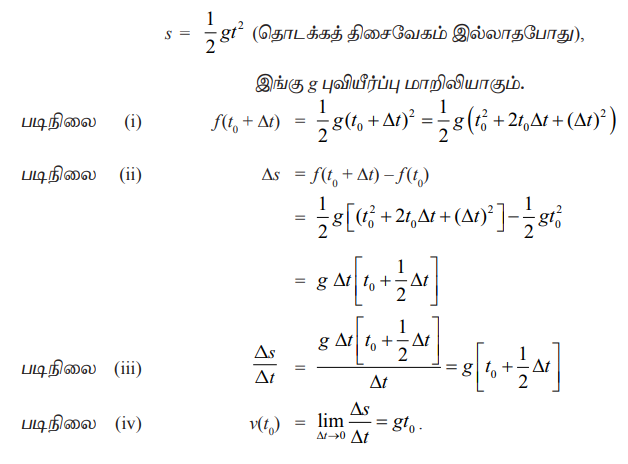
இதிலிருந்து, t0, கணநேரத்தில் முழுமையாகத் திசைவேகம் வரையறுக்கப்பட்டுள்ளது என்பது தெளிவாகிறது. மேலும் இது இயக்க நேரத்திற்கு விகித சமமாக அமைகின்றது.

3. சார்பின் வகைக்கெழு அல்லது வகையிடல் (The derivative of a Function)

இப்போது நாம் நுண் கணிதத்தின் மிக முக்கியமான தருணத்திற்கு வந்துள்ளோம். எல்லை மூலமாகத் தொடுகோட்டின் சாய்வை வரையறுத்தல் அல்லது எல்லை மூலமாகத் தடையின்றி விழும் பொருளின் கணநேரத் திசைவேகத்தினைக் காணுதல், என்பது வகை நுண்கணிதத்தில் உள்ள இரு அடிப்படைச் செயல்பாடுகளில் ஒன்றான வகையிடல் ஆகும்.

வரையறை 10.2

x0 என்ற புள்ளி அமைந்துள்ள ஒரு திறந்த இடைவெளியான I ⊆ ℝ -ல் ƒ என்ற சார்பு வரையறுக்கப்படுகிறது. மேலும் 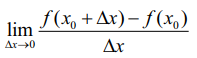  என்பது கிடைக்கப்பெறும் என்க.

இப்போது ƒ என்பது x0 -ல் வகையிடத்தக்கது எனவும், x0 -ல் ƒ-ன் வகைக்கெழு என்பது ƒ'(x0) எனக் குறிக்கப்பட்டு பின்வருமாறு அமைகிறது.

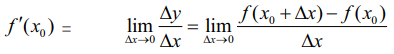
இந்த எல்லையானது கிடைக்கப்பெறும் அனைத்து x -ன் மதிப்புகளுக்கும் 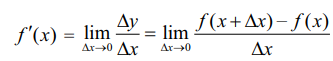என்பது x -ன் சார்பாக அமையும்.

x -ஆல் ஆன சார்பின் வகைக்கெழுவும் x-ஆல் ஆன சார்பாக அமைவதை உறுதி செய்ய முடியும். இந்தப் “புதிய சார்பு” (x,ƒ(x)),எனும் புள்ளியில் ƒ என்ற வளைவரையின் தொடுகோட்டின் சாய்வினைக் கொடுப்பதாக அறியலாம். (அந்தப் புள்ளியில் தொடுகோட்டை வரைய முடியுமெனில்)

ஒரு சார்பின் வகைக்கெழுவைக் காணும் முறையினை வகையிடல் என அழைக்கிறோம். ஒரு சார்பு x-ல் வகையிடத்தக்கதாக (வகைமையாக) இருக்க, x-ல் அதன் வகைக்கெழு இருத்தல் வேண்டும். மேலும் திறந்த இடைவெளியான (a, b)-ல் வகைமையாக இருக்க வேண்டுமாயின் (a,b)-ல் உள்ள ஒவ்வொரு புள்ளியிலும் வகைமையாக இருத்தல் வேண்டும்.

y = ƒ(x)-ன் வகைக்கெழுவைக் குறிக்க, ƒ' (x) "ƒ prime of x” அல்லது “ƒ dash of x” என்பது மட்டுமன்றி பிற குறியீடுகளும் பயன்படுத்தப்படுகின்றன. அவற்றில் சில,

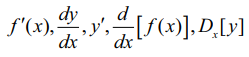அல்லது Dy அல்லது y1. இங்கு d/dx அல்லது D என்பது வகையிடல் செயலி ஆகும்.

இங்கு dy/dx என்பதை “dy - dx”, அல்லது “Dee y Dee x” அல்லது “Dee Dee x of y” எனவும் படிக்கலாம். இக்குறியீடு ஒரு பின்னத்தை குறிக்காது என்பதை நினைவில் நிறுத்தவும்.

dy / dx என்ற குறியீட்டினை லிபினிட்ஸ் குறியீடு என்பர்.

4. ஒரு பக்க வகைக்கெழுக்கள் (இடப்பக்க மற்றும் வலப்பக்க வகைக்கெழு) One sided derivatives (left hand and right hand derivatives)

x0 எனும் புள்ளியினை உடைய திறந்த இடைவெளியான (a, b)-ல் y = ƒ(x) எனும் சார்பு வரையறுக்கப்படுகிறது. x = x0 –ல்ƒ-ன் இடப்பக்க வகைக்கெழுவும் வலப்பக்க வகைக்கெழுவும் முறையே ƒ'(x0-) மற்றும் ƒ'(x0+), எனக் குறிக்கப்பட்டுக் கீழ்க்காணுமாறு வரையறுக்கப்படுகிறது. 

எல்லைகள் கிடைக்கும் பட்சத்தில்

வரையறை 10.3

[a, b] என்ற மூடிய இடைவெளியில் சார்பு ƒ வகைமையானது எனக்கூற வேண்டுமானால், சார்பு ƒ ஆனது (a, b) எனும் திறந்த இடைவெளியில் வகைமையானதாகவும், மேலும் இறுதிப்புள்ளியான a மற்றும் b-ல்

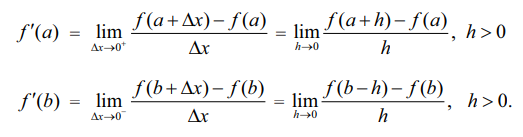
x = x0 என்ற புள்ளியில் ƒவகையிடத்தக்கதாக இருப்பின் 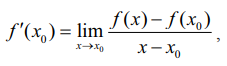  இங்கு  x = x0 + ∆x மற்றும் ∆x → 0 என்பது x → x0 -க்கு சமானம் ஆகும். இத்தகைய மாற்று முறை சில நேரங்களில் வகைமையைக் கணக்கிட எளிதாக அமையும்.

வசதிக்கேற்ப, h = ∆x, என எடுத்துக்கொண்டால் எல்லை கிடைக்கப்பெறின், 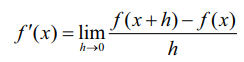  ஆகும்.