வரையறை, தேற்றம் - தளத்தின் ஒரு செங்கோடு மற்றும் ஆதிப்புள்ளியிலிருந்து தளத்திற்கு உள்ள தூரம் கொடுக்கப்பட்டால் தளத்தின் சமன்பாடு (Equation of a plane when a normal to the plane and the distance of the plane from the origin are given) | 12th Maths : UNIT 6 : Applications of Vector Algebra

12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்

தளத்தின் ஒரு செங்கோடு மற்றும் ஆதிப்புள்ளியிலிருந்து தளத்திற்கு உள்ள தூரம் கொடுக்கப்பட்டால் தளத்தின் சமன்பாடு (Equation of a plane when a normal to the plane and the distance of the plane from the origin are given)

தளத்தின் ஒரு செங்கோடு மற்றும் ஆதிப்புள்ளியிலிருந்து தளத்திற்கு உள்ள தூரம் கொடுக்கப்பட்டால் தளத்தின் சமன்பாடு (Equation of a plane when a normal to the plane and the distance of the plane from the origin are given) : (a) செங்கோட்டு வடிவ வெக்டர் சமன்பாடு (Vector equation of a plane in normal form) (b) செங்கோட்டு வடிவ கார்டீசியன் சமன்பாடு (Cartesian equation of a plane in normal form)

1. தளத்தின் ஒரு செங்கோடு மற்றும் ஆதிப்புள்ளியிலிருந்து தளத்திற்கு உள்ள தூரம் கொடுக்கப்பட்டால் தளத்தின் சமன்பாடு (Equation of a plane when a normal to the plane and the distance of the plane from the origin are given)

(a) செங்கோட்டு வடிவ வெக்டர் சமன்பாடு (Vector equation of a plane in normal form)

தேற்றம் 6.15

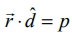ஆதிப்புள்ளியிலிருந்து தளத்திற்கு உள்ள தூரம் p மற்றும் தளத்திற்குச் செங்குத்தான ஓரலகு வெக்டர் எனில், தளத்தின் சமன்பாடு ஆகும்.

நிரூபணம்

ஆதிப்புள்ளியிலிருந்து p தொலைவில் உள்ள தளத்தினை கருதுக. ஆதிப்புள்ளி O−விலிருந்து தளத்திற்கு வரையப்படும் செங்கோட்டின் அடி A என்க.

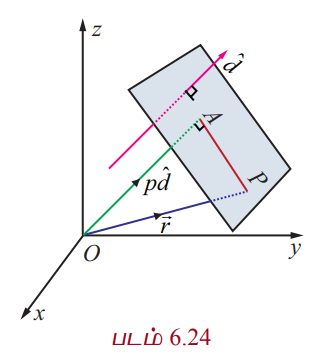
−ன் திசையில் உள்ள ஓரலகு செங்குத்து வெக்டர் என்க. பின்னர், 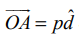ஆகும்.

என்பது தளத்தில் உள்ள ஏதேனும் ஒரு புள்ளி P−ன் நிலைவெக்டர் எனில், 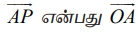வுக்குச் செங்குத்தாகும்.

எனவே,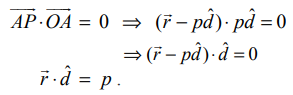

இச்சமன்பாடு, தளத்தின் செங்கோட்டு வடிவ வெக்டர் சமன்பாடு எனப்படும்.

(b) செங்கோட்டு வடிவ கார்டீசியன் சமன்பாடு (Cartesian equation of a plane in normal form)

–ன் திசைக்கொசைன்கள் 1,m,n என்க. எனவே, 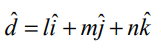ஆகும்.

இதனைச் சமன்பாடு (1)−ல் பிரதியிட,

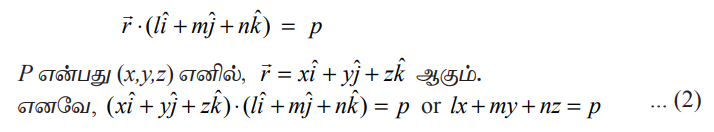
சமன்பாடு (2) ஆனது தளத்தின் செங்கோட்டு வடிவ கார்டீசியன் சமன்பாடு எனப்படும்.

குறிப்புரை

(i) ஆதிப் புள்ளி வழியாக தளம் செல்லுமெனில், p = 0 ஆகும். எனவே, தளத்தின் சமன்பாடு lx + my + nz = 0.

(ii) என்பது தளத்திற்கு செங்குத்தான வெக்டர் எனில், 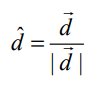என்பது தளத்திற்குச் செங்குத்தான ஓரலகு வெக்டராகும். எனவே, தளத்தின் சமன்பாடு 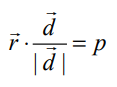அல்லது 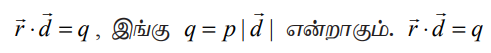என்ற சமன்பாடு தளத்தின் திட்ட வடிவ வெக்டர் சமன்பாடு எனப்படும்.

குறிப்பு

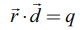என்ற திட்ட வடிவச் சமன்பாட்டில், என்பது ஓரலகு செங்குத்து வெக்டராகவோ, q என்பது செங்குத்துத் தொலைவாகவோ இருக்கத் தேவையில்லை.

Tags : Definition, Theorem, Proof வரையறை, தேற்றம்.

12th Maths : UNIT 6 : Applications of Vector Algebra : Equation of a plane when a normal to the plane Definition, Theorem, Proof in Tamil : 12th Standard Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் : தளத்தின் ஒரு செங்கோடு மற்றும் ஆதிப்புள்ளியிலிருந்து தளத்திற்கு உள்ள தூரம் கொடுக்கப்பட்டால் தளத்தின் சமன்பாடு (Equation of a plane when a normal to the plane and the distance of the plane from the origin are given) - வரையறை, தேற்றம் : 12 ஆம் வகுப்பு புத்தகம் கேள்விகள் மற்றும் பதில்கள்.