எடுத்துக்காட்டு கணக்குகள், பயிற்சி கணக்குகள்

எடுத்துக்காட்டு 8.1

ஹைட்ரஜன் அணுவின் 5வது சுற்றுப்பாதையின் ஆரம் 13.25 Å எனில், அச்சுற்றுப்பாதையில் உள்ள எலக்ட்ரானின் அலைநீளத்தைக் கணக்கிடுக.

தீர்வு

2 π r = nλ

2x 3.14 X 13.25Å = 5x λ

λ = 16.64Å

எடுத்துக்காட்டு 8.2

ஹைட்ரஜன் அணுவின் 5வது சுற்றுப்பாதையின் (i) கோண உந்தம் மற்றும் (ii) அதிலுள்ள எலக்ட்ரானின் திசைவேகம் ஆகியவற்றைக் கணக்கிடுக.

(h = 6.6x 10-34Js, m = 9.1 X 10-31 kg)

தீர்வு

எடுத்துக்காட்டு 8.3

அ) முதல் போர் சுற்றுப்பாதையில், எலக்ட்ரானின் திசைவேகம் ஒளியின் திசைவேகம் இடையேயான தகவு பரிமாணம் இல்லாத ஒரு எண் என்பதை நிறுவுக.

ஆ) போர் அணுமாதிரியில் அடிநிலை, முதல் கிளர்வு நிலை மற்றும் இரண்டாவது கிளர்வு நிலைகளில் உள்ள எலக்ட்ரான்களின் திசைவேகங்களைக் கணக்கிடுக.

தீர்வு :

n ஆவது சுற்றுப்பாதையில் எலக்ட்ரானின் திசைவேகம்

p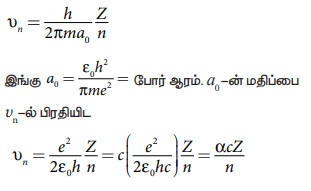

இங்கு c என்பது வெற்றிடத்தில் ஒளியின் திசைவேகம், இதன் மதிப்பு c = 3 x 108 m s-1 மற்றும் a என்பது நுண்வரியமைப்பு மாறிலி (fine structure constant).

ஹைட்ரஜன் அணுவுக்கு Z=1 மற்றும் முதல் சுற்றுப்பாதைக்கு n=1. எனவே முதல் சுற்றுப்பாதையில் எலக்ட்ரானின் திசை வேகத்திற்கு வெற்றிடத்தில் ஒளியின் மேலும் திசைவேகத்திற்கு இடையேயான தகவு

p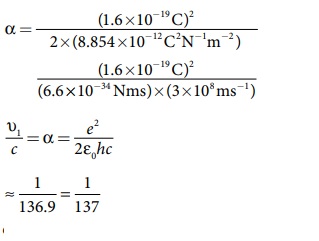

இது ஒரு பரிமாணம் இல்லாத எண் ஆகும்.

=> a = 1/137

ஆ) நுண்வரியமைப்பு மாறிலியைப் பயன்படுத்தி, எலக்ட்ரானின் திசைவேகத்தைப் பின்வருமாறு எழுதலாம்

⇒ α = 1/137

ஹைட்ரஜன் அணுவுக்கு Z = 1. எனவே n ஆனது சுற்றுப்பாதையில், எலக்ட்ரானின் திசைவேகம்

υn = αcZ / n

முதல் சுற்றுப்பாதையில் (அடிநிலை), எலக்ட்ரானின் திசைவேகம்

υn = c/137 × 1/n = (2.19×106) × 1/n  ms−1

இரண்டாவது சுற்றுப்பாதையில் (முதல் கிளர்வு நிலை), எலக்ட்ரானின் திசைவேகம்

υ = 2.19×106 ms−1

மூன்றாவது சுற்றுப்பாதையில் (இரண்டாவது கிளர்வு நிலை), எலக்ட்ரான் திசைவேகம்

 υ2 = 1.095×106 ms−1

இதிலிருந்து, υ1 > υ2 > υ3

எடுத்துக்காட்டு 8.4

அணுக்கரு நிலையாகவும் அணுக்கருவைச் சுற்றி எலக்ட்ரான்கள் இயங்குவதாகவும் கருத்தில் கொண்டு போர் அணுமாதிரியின் சமன்பாடுகள் தருவிக்கப்பட்டுள்ளன. அணுக்கருவும் இயக்கத்தில் உள்ளதாகக் கருதினால், அத்தகைய அமைப்பில் ஆற்றலின் கோவையைத் தருவிக்கவும்.

தீர்வு

எலக்ட்ரானின் நிறை m மற்றும் அணுக்கருவின் நிறை M என்க. புறவிசை ஏதும் இவ்வமைப்பின் மீது புறவிசை ஏதும் செயல்படாததால், ஹைட்ரஜன் அணுவின் நிறை மையம் நிலையாக இருக்கும். எனவே, நிறையின் மையத்தைப் பொருத்து அணுக்கருவும் எலக்ட்ரானும் இயக்கத்தில் இருக்கும் (படம் 8.21).

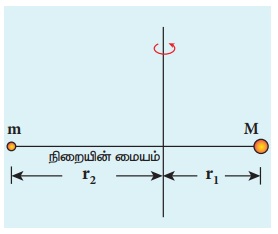
எலக்ட்ரானின் திசைவேகம் v மற்றும் அணுக்கருவின் திசைவேகம் V என்க. இவ்வமைப்பின் மொத்த நேர்க்கோட்டு உந்தம் சுழி ஆகும். எனவே,

அமைப்பின் நிலை மின்னழுத்த ஆற்றல் எந்த மாறுபாடும் அடையவில்லை ஆதலால், நிறைக்குப் பதிலாக சுருக்கிய நிறையைப் பதிலீடு செய்து ஹைட்ரஜன் அணுவின் மொத்த ஆற்றலைப் பெறலாம்.

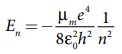
எலக்ட்ரானின் நிறையைக் காட்டிலும் அணுக்கருவின் நிறை மிக அதிகமாதலால், சுருக்கிய நிறையின் மதிப்பு ஆனது எலக்ட்ரானின் நிறைக்கு ஏறத்தாழ சமமாகும்.

எடுத்துக்காட்டு 8.5

ஹைட்ரஜனைப் போன்றதொரு அணு ஒன்றின் ஆற்றல் pppppppppp எனில் பின்வருவனவற்றைக் கணக்கிடவும். இங்கு nEN

அ) அந்த அணுவின் ஆற்றல் மட்டங்களை வரையவும்; மேலும் அதன் அணு எண்ணைக் கணக்கிடவும்.

ஆ) அணு அடிநிலையில் உள்ளது எனில், அதன் முதல் கிளர்வு மின்னழுத்தம் மற்றும் அயனியாக்க மின்னழுத்தம் ஆகியவற்றைக் கணக்கிடுக.

இ) முறையே 42 eV மற்றும் 56 eV ஆற்றல் கொண்ட இரு போட்டான்களை அந்த அணுவின் மீது மோதச் செய்தால், அவற்றை அந்த அணு உட்கவருமா?

ஈ) முதல் போர் சுற்றுப்பாதையின் ஆரத்தைக் கண்டறிக.

உ) அடிநிலையில் அதன் இயக்க மற்றும் மின்னழுத்த ஆற்றல்களைக் கணக்கிடுக.

தீர்வு

அ) En =-54.4/n2 eV எனவே,

n = 1 எனில், அடிநிலை ஆற்றல்

n = 2 எனில், E2 = -13.6 ev; E3 = -6.04 eV, E4. = -3.4 eV அதேபோல் மற்றவை

Z என்பது அணு எண்; கொடுக்கப்பட்டுள்ள ஆற்றல் மதிப்பை ஒப்பிடும் போது, -13.6 Z2 = - 54.4 =>

Z=±2 அணு எண் எதிர்க்குறி எண்ணாக இருக்க  முடியாது. எனவே Z = 2.

இ) முதல் கிளர்வு ஆற்றல்

E1 = E2 - E1 =-13.6eV- (-54.4eV)

= 40.8eV

எனவே முதல் கிளர்வு மின்னழுத்தம்

ஈ) இரு போட்டான்களை A மற்றும் B என்க. போட்டான் A-வின் ஆற்றல் 42 eV மற்றும் போட்டான் B-ன் ஆற்றல் 51 eV.

போர் கொள்கையின் படி, ஆற்றல் மட்டங்களுக்கு இடையேயான வேறுபாட்டுக்குச் சமமான ஆற்றல் கொண்ட போட்டானை அணு உட்கவரும்; சமமாக இல்லையெனில், உட்கவராது.

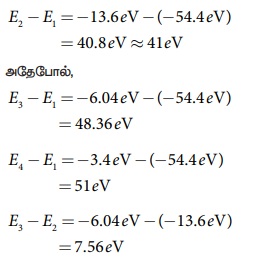
அதேபோல் அடுத்தடுத்தவை

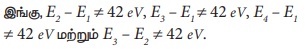 எந்தவொரு வாய்ப்பிலும் (42 eV) போட்டான் ஆற்றல் மதிப்பின் முழு மடங்குக்குச் சமமான ஆற்றல் வேறுபாடு அமையாததால், போட்டான் A இந்த அணுவால் உட்கவரப்படுவதில்லை. ஆனால், போட்டான் Bயைப் பொருத்தவரை, E4 – E1 = 51 eV, ஆகையால், இவ்வணுவால், போட்டான் B உட்கவரப்படுகின்றது.

உ) போர் அணுமாதிரியில், மொத்த ஆற்றலானது இயக்க ஆற்றலின் எதிர்க்குறி மதிப்புக்குச் சமம் ஆதலால்,

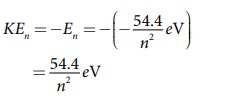
நிலைமின்னழுத்த ஆற்றலானது இயக்க ஆற்றலின் எதிர்க்குறி மதிப்பின் இரு மடங்காகும். எனவே,

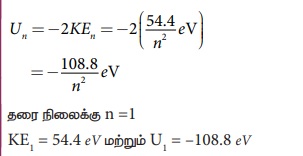
எடுத்துக்காட்டு 8.6

குளோரினின் பல்வேறு ஐசோடோப்புகளுக்கு இடையே வேறுபாடுகள் இல்லையெனில், அவற்றின் சராசரி அணு நிறையைக் கணக்கிடுக.

தீர்வு

குளோரின் தனிமமானது 75.77% 3517CI மற்றும் 24.23% 3717CI ஆகியவற்றின் கலவையே. எனவே, அதன் சராசரி அணுநிறை

ஒரு தனிமத்தின் இந்த சராசரி அணுநிறை அல்லது வேதிய அணு எடை (குளோரினுக்கு இதன் மதிப்பு 35.453u) மதிப்புகளையே வேதியியலாளர்கள் (Chemists) பயன்படுத்துகின்றனர். எனவே, தனிம வரிசை அட்டவணையில் குறிப்பிடப்பட்டுள்ள அணு நிறை மதிப்புகள் இவ்வாறு கணக்கிடப்பட்ட சராசரி அணுநிறை மதிப்புகளே என்பதைக் கருத்தில் கொள்ளவும்.

எடுத்துக்காட்டு 8.7

19779Au அணுக்கருவின் ஆரத்தைக் கணக்கிடுக.

தீர்வு

சமன்பாடு (8.19)-ன் படி,

R = 1.2X10-15 X (197)1/3 = 6.97 X 10-15 M-

அல்லது R = 6.97 F

எடுத்துக்காட்டு 8.8

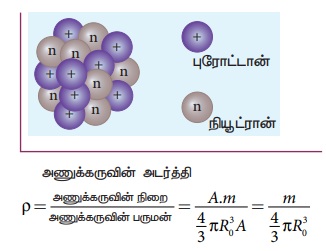
நிறை எண் A கொண்ட அணுக்கருவின் அடர்த்தியைக் கணக்கிடுக.

தீர்வு

சமன்பாடு (8.19)ன்படி, அணுக்கருவின் ஆரத்திற்கான

புரோட்டானுக்கும் நியூட்ரானுக்கும் இடையேயுள்ள நிறை வேறுபாட்டைப் புறக்கணித்தால், நிறை எண் A கொண்ட அணுக்கருவின் நிறை A.m, இங்கு m என்பது புரோட்டானின் நிறை = 1.6726 x 10-27 kg.

எடுத்துக்காட்டு 8.9

பின்வரும் தகவல்களைப் பயன்படுத்தி 42He அணுக்கருவின் பிணைப்பு ஆற்றலைக் கணக்கிடுக: ஹீலியம் அணுவின் அணு நிறை MA (He) = 4.00260u மற்றும் ஹைட்ரஜன் அணுவின் நிறை mH = 1.00785u.

தீர்வு :

பிணைப்பு ஆற்றல் BE =[zmH + Nmn - MA ]c2

ஹீலியம் அணுவிற்கு Z=2, N=A-Z=4-2=2

நிறை குறைபாடு

எடுத்துக்காட்டு 8.10

24He அணுக்கருவின் ஒரு நியூக்ளியானுக்கான பிணைப்பாற்றலைக் கணக்கிடு.

தீர்வு

எடுத்துக்காட்டு 8.9 லிருந்து , 24He -ன் BE = 28 MeV

ஒரு நியூக்ளியானுக்கான பிணைப்பாற்றல் =  

= 28 MeV/4 = 7 MeV.

எடுத்துக்காட்டு 8.11

(அ) ஓய்வு நிலையிலுள்ள 23292U அணுக்கருவானது a-துகளை வெளிவிடுவதன் மூலம் 22890Th அணுக்கருவாக சிதையும் நிகழ்வில் சிதைவு ஆற்றலைக் கணக்கிடுக. அணுநிறைகள் பின்வருமாறு : 23292U = 232.037156u, 22890Th = 228.028741u, 23292e = 4.002603u

(ஆ) 22890Th மற்றும் a-துகள் ஆகியவற்றின் இயக்க ஆற்றல் மற்றும் அவற்றின் தகவு ஆகியவற்றைக் கணக்கிடு.

தீர்வு

நிறை குறைபாடு Δm = (mu - mTh - ma)

= (232.037156-228.028741 - 4.002603)u

இச்சிதைவின் போது ஏற்படும் நிறை இழப்பு = 0.005812u

lu=931MeV, ஆதலால், வெளிவிடப்படும் ஆற்றல்

Q= (0.0058121u) x (931MeV/u)

= 5.41 MeV

இச்சிதைவு ஆற்றல் Q வானது, a துகள் மற்றும் சேய் அணுக்கரு ஆகியவற்றின் இயக்க ஆற்றலாகத் தோன்றுகிறது.

(அ) எந்தவொரு சிதைவு நிகழ்விலும் மொத்த நேர்க்கோட்டு உந்தம் மாறாமல் இருக்க வேண்டும்.

தாய் அணுக்கருவின் மொத்த நேர்க்கோட்டு உந்தம் = சேய் அணுக்கரு மற்றும் a- துகளின் மொத்த நேர்க்கோட்டு உந்தம். இந்த நேர்வில், சிதைவுக்கு முன் யுரேனியம் அணுக்கரு ஓய்வு நிலையில் இருப்பதால், அதன் நேர்க்கோட்டு உந்தம் சுழியாகும். உந்தம் மாறா விதியின் படி,

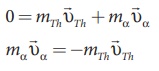
a - துகளும் சேய் அணுக்கருவும் எதிரெதிர் திசையில் செல்கின்றன என்பதை இது காட்டுகிறது.

mava = mTh vTh (எண்ம திப்பில்,)

a-துகளின் வேகம் . = υα = mThυTh

இங்கு mTh / ma > 1. ஆகையால் va > vTh மேலும்

a- துகள் மற்றும் சேய் அணுக்கரு இவ்விரண்டின் இயக்க ஆற்றல் தகவு

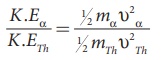
மேலேயுள்ள சமன்பாட்டில் va ஐப் பிரதியிட,

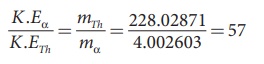
a- துகளின் இயக்க ஆற்றல் சேய் அணுக்கருவின் (3Th) இயக்க ஆற்றலை விட 57 மடங்கு அதிகம். சிதைவு ஆற்றல் Q = விளைவுப் பொருள்களின் மொத்த இயக்க அற்றல்

K.Eα + K.ETh = 5.41MeV

57K.ETh + K.ETh = 5.41MeV

K.ETh = 5.41/58 MeV = 0.093MeV

K.Eα = 57K.ETh = 57×0.093 = 5.301MeV

மொத்த இயக்க ஆற்றலில் கிட்டத்தட்ட 98% அளவு a துகளால் எடுத்துக்கொள்ளப்படுகிறது.

எடுத்துக்காட்டு 8.12

தொடக்கத்திலுள்ள கதிரியக்கக் கார்பன்-14 அணுக்களின் எண்ணிக்கை 10,000 எனில், 22,920 ஆண்டுகளுக்குப் பிறகு சிதைவடையாமல் இருக்கும் அணுக்களின் எண்ணிக்கையைக் கணக்கிடுக. கார்பன்-14ன் அரை ஆயுட்காலம் 5730 ஆண்டுகள்.

தீர்வு

அரை ஆயுட்காலங்களின் அடிப்படையில் கால இடைவெளியைக் கணக்கிட,

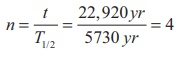
22,920 ஆண்டுகளுக்குப் பிறகு சிதைவடையாமல் இருக்கும் அணுக்களின் எண்ணிக்கை,

N = ( ½ )0 N0 = (1/2)4 ×10, 000

N = 625

எடுத்துக்காட்டு 8.13

அரை ஆயுட்காலம் 10 நிமிடம் கொண்ட ஒரு கதிரியக்கப் பொருளின் சிறு அளவில், 2.6μg கலப்படமில்லா 137N உள்ளது. (அ) தொடக்கத்தில் உள்ள அணுக்களின் எண்ணிக்கை எவ்வளவு? (ஆ) தொடக்கத்தில் கதிரியக்கச் செயல்பாடு எவ்வளவு? (இ) 2 மணி நேரத்திற்குப் பிறகு செயல்பாடு எவ்வளவு? (ஈ) இப்பொருளின் சராசரி ஆயுள் எவ்வளவு?

தீர்வு

(அ) N0.ன் மதிப்பைக் கணக்கிட முதலில் 2.6μgல் உள்ள 137N அணுக்களின் எண்ணிக்கையைக் கணக்கிட வேண்டும். நைட்ரஜனின் அணு நிறை 13 ஆதலால், 13 g அளவிலான 137N ல் அவகேட்ரோ எண்ணிற்குச் சமமான அணுக்கள் இருக்கும்.

1கிராம் உள்ள அணுக்களின் 137N எண்ணிக்கை 6.02 x 1023 / 13 - எனில், 2.6μg ல் உள்ள தொடக்க

137N அணுக்களின் எண்ணிக்கை

எடுத்தக்காட்டு 8.14

கீழடி என்ற சிறிய கிராமம் தமிழ்நாட்டிலுள்ள மிகவும் முக்கியமான அகழ்வாராய்ச்சி நடைபெறும் பகுதிகளில் (படம்) ஒன்றாகும். இது சிவகங்கை மாவட்டத்தில் அமைந்துள்ளது. (தங்க நாணயங்கள், மண்கலன்கள், மணிகள், இரும்புக் கருவிகள், அணிகலன்கள் மற்றும் மரக்கரித்துண்டு உள்ளிட்ட) பல தொல் கைவினைப் பொருள்கள் கீழடியில் கண்டெடுக்கப்பட்டுள்ளன. இதன் மூலம் வைகை ஆற்றங்கரைகளில் பண்டைய நாகரிகம் செழித்திருந்தது என்பதற்கான தகுந்த ஆதாரம் கிடைத்துள்ளது. இப்பொருள்களின் காலத்தைக் கணிப்பதற்கு , (படத்தில் கொடுக்கப்பட்டுள்ள) 200 g கரியானது கார்பன் காலக்கணிப்பு சோதனைக்கு உட்படுத்தப்படுகிறது. அதில் 146C இன் செயல்பாடு 38 சிதைவுகள்/ எனில், அக்கரியின் வயதைக் கணக்கிடுக.

படம் (அ) கீழடி அகழ்வாய்வுப் பகுதி

படம் (ஆ) கார்பன் காலக்கணிப்பிறகு அனுப்பப்பட்ட கரித்துண்டு

தீர்வு

கரியின் வயதைக் கணக்கிட, அது மரமாக உயிரோடு இருந்த போது, அதன் தொடக்க கதிரியக்கச் செயல்பாடு (R0) தெரிய வேண்டும்.

மாதிரிப் பொருளின் கதிரியக்கச் செயல்பாடு

அதன் காலம் t ஐக் கண்டறிய, சமன்பாடு (1)ஐப்

பின்வருமாறு எழுதலாம்,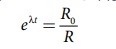 

இரு புறமும் மடக்கை எடுக்க, நமக்கு கிடைப்பது

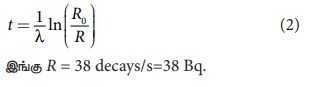
இங்கு R = 38 decays/s=38 Bq.

சிதைவு மாறிலியைக் கணக்கிட பின்வரும் சமன்பாட்டைப் பயன்படுத்தலாம்:

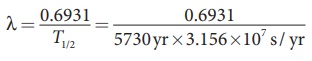
[∴ 1yr = 365.25 × 24 × 60 × 60 s = 3.156 × 107 s]

λ = 3.83×10−12 s−1

தொடக்க கதிரியக்கச் செயல்பாடு R0 ஐக் கண்டுபிடிக்க, R0 = λN0 என்ற சமன்பாட்டைப் பயன்படுத்துவோம். இங்கு N0. என்பது மாதிரிப் பொருள் பயன்பாட்டில் இருந்தபோது அதிலிருந்த கார்பன்-14 அணுக்களின் எண்ணிக்கையாகும். கரியின் நிறை 200 g. 12 g கார்பனில் 6.02X1023 கார்பன் அணுக்கள் இருக்கும். எனவே, 200 g-ல்

6.02X1023 அணுக்கள் / மோல் / 12கி / மோல்

X 200 ͠ 1 X10 - அணுக்கள்

(மாதிரிப் பொருளான) அதாவது மரம் உயிருடன் இருந்தபோது, 146C: 126C -இன் விகிதம் 1.3x10-12 எனவே கார்பன்-14 அணுக்களின் மொத்த எண்ணிக்கை,

N0 =1x1025X1.3x10-12 =1.3x113 அணுக்கள்

தொடக்க செயல்பாடு,

R0 =3.83 x1012 X 1.3x10-13 ͠ 50சிதைவுகள் / s

= 50Bq

R0 மற்றும் λ மதிப்புகளை சமன்பாடு (2)ல் பிரதியிட,

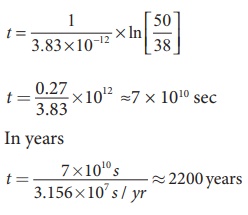
இந்த அகழ்வாய்வில் கண்டெடுக்கப்பட்ட பொருள்கள் தமிழ்நாடு அரசின் தொல்லியல் துறையினரால் அமெரிக்காவிற்கு அனுப்பப்பட்டு கார்பன் காலக்கணிப்பு செய்ததில், கீழடியில் கண்டெடுக்கப்பட்ட கைவினைப் பொருள்களின் வயது 2200 ஆண்டுகளிலிருந்து 2500 ஆண்டுகள் இருக்கும் (சங்க காலம் - கி.மு. (பொ.ஆ.மு ) 400 முதல் கி.மு. (பொ.ஆ.மு ) 200) என்பது அறிக்கை மூலமாக உறுதிப்படுத்தப்பட்டுள்ளது. 2000 ஆண்டுகளுக்கு முன்னரேயே தமிழகத்தில் நகர்ப்புற நாகரிகம் இருந்துள்ளதை கீழடி அகழ்வாராய்ச்சி அறிவியல் பரிசோதனை வாயிலாக நிறுவியுள்ளது.

எடுத்துக்காட்டு 8.15

1kgநிறையுள்ள 23592U பிளவுறும் போது வெளிப்படும் ஆற்றலைக் கணக்கிடுக. 

தீர்வு :

100 W ஒளி விளக்கு ஒன்றினை 30,000 ஆண்டுகள் இயக்குவதற்குத் தேவையான அளவிற்கு இது மிகப்பெரிய அளவிலான ஆற்றலாகும். வேதிவினைகளின் மூலம் இவ்வாற்றலைப் பெற வேண்டுமானால் 20,000 டன் TNT (டிரை நைட்ரோ டொலுவீன்) ஐ வெடிக்கச் செய்ய வேண்டும்.

IV. பயிற்சிக் கணக்குகள்

1. அடிநிலையிலுள்ள HA மற்றும் HB ஆகிய இரு ஹைட்ரஜன் அணுக்களைக் கருதவும். HA ஓய்வு நிலையில் உள்ளது. குறிப்பிட்ட வேகத்துடன் இயங்கும் HB அணு ஓய்வு நிலையிலுள்ள HA அணுவின் மீது நேருக்கு நேர் மோதுகிறது. மோதலுக்குப்பின் அவையிரண்டும் ஒன்றாக இணைந்து இயங்குகின்றன. இவ்விரு ஹைட்ரஜன் அணுக்களில் ஏதேனும் ஒன்று கிளர்வு நிலையை அடைய வேண்டும் என்றால் இயக்கத்தில் உள்ள HB ஹைட்ரஜன் அணுவின் குறைந்தபட்ச இயக்க ஆற்றலைக் கணக்கிடுக.

தீர்வு:

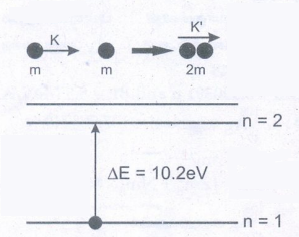
நேர்க்கோடு உந்த அழிவின்மைவிதிபடி. p = p' 

√2km = √[ 2k'(2m) ] 

(அல்லது) K = 2K' ...... (1)

ஆற்றல் அழிவின்மை விதிபடி,

K = K' + ∆E ........(2)

சமன்பாடு (1) மற்றும் (2) யை சமன்படுத்துவதன் மூலம்

∆E =K/2

முதல் கிளர்வு ஆற்றல் = E2 – E1 = 10.2 eV 

∆E ≥ 10.2eV

K/2 ≥ 10.2

K ≥ 20.4 eV

விடை : 20.4eV 

2. போர் அணு மாதிரியில், நிலைமாற்றங்களின் (transitions) அதிர்வெண் பின்வரும் சமன்பாட்டினால் அறியப்படுகிறது. 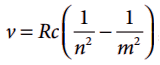, இங்கு n < m, பின்வரும் நிலை மாற்றங்களைக் கருதுக. 

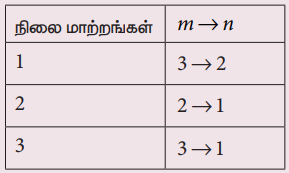
இந்நிலை மாற்றங்களின் அதிர்வெண் கூட்டல் விதிக்கு (இவ்விதி ரிட்ஸ் சேர்க்கைத் தத்துவம் என்றழைக்கப்படுகிறது) உட்படும் என்பதை நிறுவுக. 

தீர்வு: 

ரிட்ஸ் சேர்க்கைத்தத்துவம் (Ritz combination principle) நிலைமாற்றங்களின் அதிர்வெண் கூட்டல் விதிக்கு உட்படும். 

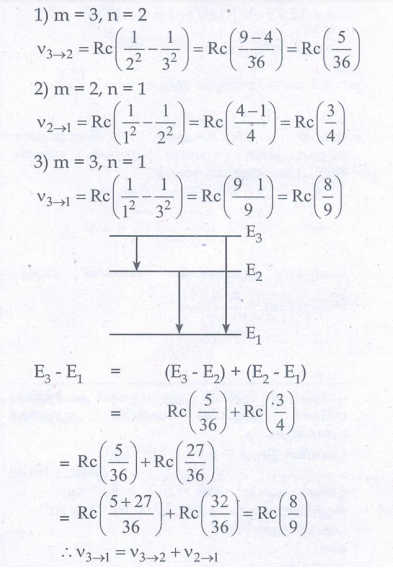
விடை: V3 → 2 + V 2 →1 = V3 → 1

3. அ) ஹைட்ரஜன் அணு ஒன்று அலைநீளம் 97.5 nm கொண்ட கதிர்வீச்சினால் கிளர்வுற செய்யப்படுகிறது. அக்கிளர்வு நிலையின் முதன்மைக் குவாண்டம் எண்ணைக் கணக்கிடுக. 

ஆ) வெளிவிடு நிறமாலையில் வரிகளின் மொத்த எண்ணிக்கை n(n–1) / 2 என்று காட்டுக. மேலும் கேள்வி (அ)-வில் கொடுக்கப்பட்டுள்ள கிளர்வு நிலையிலிருந்து கிடைக்கும் வெளிவிடு நிறமாலையில் சாத்தியமாகும் வரிகளின் எண்ணிக்கையைக் கணக்கிடுக.

தகவல் : λ = 97.5nm= 97.5 × 10−9 m = 975 × 10−10 m

தீர்வு :

ஆற்றல் E = hc / λ

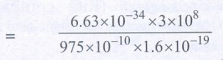
= 12.75 eV                [1eV = 1.6 × 10−19J]

En = −13.6/n2 eV

n = 1 எனில், அடிநிலை ஆற்றல் E1 = − (13.6 / l2)

E1 = −13.6 /n2 eV

ஆற்றல் மட்டங்களுக்கு இடையேயான வேறுபாட்டுக்குச் சமமான ஆற்றல் கொண்ட போட்டானை அணு உட்கவரும்

En = −13.6 + 12.75 = −0.85 eV

n2 = −13.6 / En = −13.6 / −0.85 = 16 n = 4 

வெளிவிடு நிறமாலையில் வரிகளின் மொத்த எண்ணிக்கை

= n (n-1) / 2 

= (4 × 3) / 2 

= 6

விடை : அ) n = 4 ஆ) ஆறு நிலைமாற்றங்கள் சாத்தியம் 

4. புவியின் அடர்த்தியும் அணுக்கருவின் அடர்த்தியும் ஒன்றாக இருப்பின் புவியின் ஆரத்தைக் கணக்கிடுக. (புவியின் நிறை = 5.97 × 1024 kg).

தகவல்: புவியின் நிறை = 5.97 × 1024 kg 

அணுக்கருவின் அடர்த்தி = 2.3 × 1017 kg/m3 

புவியின் ஆரம் R = ? 

தீர்வு :

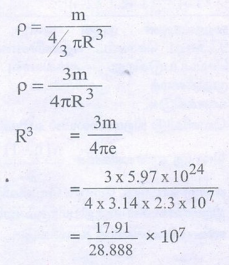
R3 = 0.62 × 107

R3 = 6.2 × 106

R = (6.2)1/3 × 102

= 1.84 × 102

R = 184m

விடை: 180m 

5. 47108Ag அணுக்கருவின் நிறை இழப்பு மற்றும் ஒரு நியூக்ளியானுக்கான பிணைப்பாற்றல் ஆகியவற்றைக் கணக்கிடவும் [47108Ag அணு நிறை Ag = 107.905949 u] 

தகவல் : 10847Ag அணுநிறை = 107.905949

தீர்வு:

BE = ∆mc2

∆m = [Zmp + Nmn − MA]

10847Ag அணுக்கருவில்

47 புரோட்டான்களையும் மற்றும்

61 நியூட்ரான்களையும் கொண்டு உள்ளது.

47 நியூட்ரான்களின் நிறை = 47 × 1.007825 u

= 47.367775 u

61 நியூட்ரான்களின் நிறை = 61 × 1.008665 u

= 61.528565 u

மொத்த நிறை = 47.367775 + 61.528565 

= 108.89634 u

நிறை இழப்பு ∆M = 108.89634 − 107.905949

∆M = 0.990391u

BE = 0.990391 u × c2

BE = 0.990391 × 931 MeV

BE/A = (0.990391 × 931) /108  MeV 

BE/A = = 8.5 MeVA

விடை:

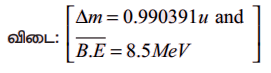
6. A மற்றும் B ஆகிய இரு கதிரியக்கத் தனிமங்களின் அரை ஆயுட்காலங்கள் முறையே 20 நிமிடங்கள் மற்றும் 40 நிமிடங்கள். தொடக்கத்தில் இவையிரண்டும் சம எண்ணிக்கையிலான அணுக்கருக்களைப் பெற்றுள்ளன எனில் 80 நிமிடங்களுக்குப்பிறகு A மற்றும் B ஆகியவற்றின் சிதைவடைந்த அணுக்கரு எண்ணிக்கைகளின் விகிதம் எவ்வளவு? 

விடை: 5 : 4 

7. அரை ஆயுட்காலம் 5.01 நாள்கள் கொண்ட சிறு அளவு 210Bi தனிமத்தின் செயல்பாட்டினை உன் பிறந்தநாளன்று அளவிடுகிறாய் என வைத்துக் கொள்வோம். தொடக்கத்தில் அதன் செயல்பாடு 1μCi 

அ) உன் அடுத்த பிறந்தநாளில் அதன் தோராயமான கதிரியக்கச் செயல்பாட்டு மதிப்பு எவ்வளவு? மேலும் 

ஆ) சிதைவு மாறிலி 

இ) சராசரி ஆயுள் மற்றும் 

ஈ) தொடக்கத்தில் இருந்த அணுக்களின் எண்ணிக்கை ஆகியவற்றைக் கணக்கிடுக. 

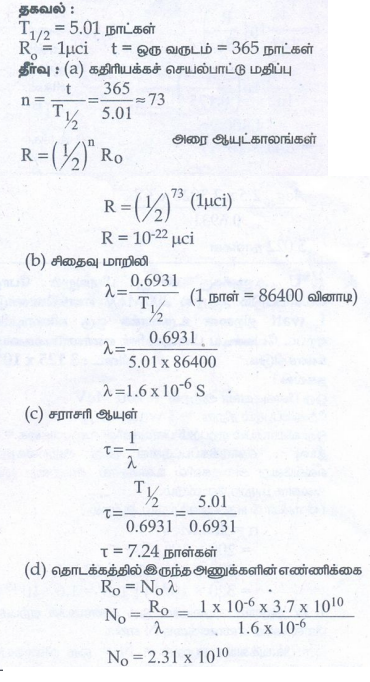
விடை: (அ) 10−22 μCi 

(ஆ) 1.6 × 10−6 s−1 

(இ) 7.24 நாட்கள் 

(ஈ) 2.31 × 1010 

8. ரேடான் உள்ள சிறு அளவு கதிரியக்கப் பொருள் 60% சிதைவடைய ஆகும் காலத்தைக் கணக்கிடுக. (ரேடானின் T1/2 = 3.8 நாள்கள்)

தகவல்: 

ரேடானின் அரை ஆயுட்காலம் = 3.8 நாள்கள் 

சிதைவடையும் பொருளின் அளவு = 60% 

எடுத்துக்கொள்ளும் காலம் =? 

தீர்வு

λ = 0.6931/3.8 நாள் சிதைவடையும் அளவு = 60%

எஞ்சியிருக்கும் அளவு = 40%

தொடக்கத்தில் உள்ள அளவு No என்க 

கதிரியக்கச்சிதைவு விதியின்படி, N = No e −λt 

N = No ல் N = 40% எனில்

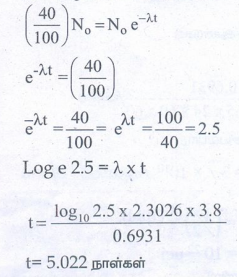
t = 5.022 நாள்கள்

விடை: 5.022 நாள்கள் 

9. 23592U அணுக்கரு ஒன்று பிளவுறும் போது வெளிப்படும் ஆற்றல் 200 MeV எனக்கொண்டு, 1 watt திறனை உருவாக்க ஒரு வினாடியில் ஏற்பட வேண்டிய பிளவுகளின் எண்ணிக்கையைக் கணக்கிடுக.

தகவல்: 

ஒரு பிளவுக்கான ஆற்றல் = 200 MeV 

தேவைப்படும் திறன் =1 watt =1J/s 

ஒரு வினாடியில் ஏற்படும் பிளவுகளின் எண்ணிக்கை =? 

தீர்வு: 

கொடுக்கப்பட்டுள்ள இரு ஆற்றல்களும் வெவ்வேறு அலகுகளில் உள்ளதால், அவற்றை ஒரே அலகாக மாற்ற வேண்டும். 

1 பிளவின் போது வெளிப்படும் ஆற்றல்

n = 200 MeV 

= 200 × 106 eV

= 200 × 106 × 1.6 × 10−19 J.

= 320 × 10−13 J              [1eV = 1.6 ×10−19 J]

1 W திறனை உருவாக்க, ஒரு வினாடியில் ஏற்படும் பிளவுகளின் எண்ணிக்கை N என்க. 

ஒரு பிளவுக்கான ஆற்றல் × N = ஒரு வினாடியில் வெளிப்படும் மொத்த ஆற்றல் 

= 320 × 10−13 × N = 1J/S

N = 1 / [320 × 10−13]  = 3.125 × 1010 பிளவுகள்

1 watt திறனை உருவாக்க, ஒரு வினாடியில் ஏற்படும் பிளவுகளின் எண்ணிக்கை 3.125 × 1010 ஆகும்

விடை: 3.125 × 1010 

10. கதிரியக்கச் செயல்பாடு 1 Ci என்றிருக்கும் ரேடியத்தின் (22688Ra) நிறை ஏறக்குறைய 1g எனக் காட்டுக. (T1/2 = 1600 ஆண்டுகள்) 

தகவல்: 

T1/2 =1600 ஆண்டுகள் 

1 கியூரி = 3.7 × 1010 சிதைவுகள்/வினாடி 

ரேடியத்தின் அளவு = ? 

தீர்வு:

11. தொல்வியல் பகுதி (archaeological site) ஒன்றிலிருந்து மரத்தின் கரித்துண்டுகள் கிடைக்கின்றன. தற்போது உயிருடன் உள்ள மரத்திலிருந்து பெறப்பட்ட சிறுபகுதியிலுள்ள கார்பன்−14 ன் அளவைப் போல் இக்கரியிலுள்ள அதேயளவு மாதிரியில் காணப்படும் கார்பன்−14 ன் அளவு 17.5% மட்டுமே உள்ளது எனில் அம்மரத்தின் வயது என்ன?

விடை: 1.44 × 104 வருடம்