பயிற்சிக் கணக்குகள்

IV. பயிற்சிக் கணக்குகள்

1. அடிநிலையிலுள்ள HA மற்றும் HB ஆகிய இரு ஹைட்ரஜன் அணுக்களைக் கருதவும். HA ஓய்வு நிலையில் உள்ளது. குறிப்பிட்ட வேகத்துடன் இயங்கும் HB அணு ஓய்வு நிலையிலுள்ள HA அணுவின் மீது நேருக்கு நேர் மோதுகிறது. மோதலுக்குப்பின் அவையிரண்டும் ஒன்றாக இணைந்து இயங்குகின்றன. இவ்விரு ஹைட்ரஜன் அணுக்களில் ஏதேனும் ஒன்று கிளர்வு நிலையை அடைய வேண்டும் என்றால் இயக்கத்தில் உள்ள HB ஹைட்ரஜன் அணுவின் குறைந்தபட்ச இயக்க ஆற்றலைக் கணக்கிடுக.

தீர்வு:

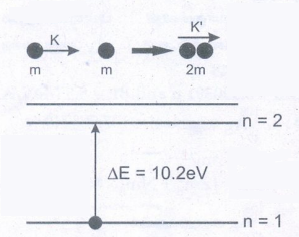
நேர்க்கோடு உந்த அழிவின்மைவிதிபடி. p = p' 

√2km = √[ 2k'(2m) ] 

(அல்லது) K = 2K' ...... (1)

ஆற்றல் அழிவின்மை விதிபடி,

K = K' + ∆E ........(2)

சமன்பாடு (1) மற்றும் (2) யை சமன்படுத்துவதன் மூலம்

∆E =K/2

முதல் கிளர்வு ஆற்றல் = E2 – E1 = 10.2 eV 

∆E ≥ 10.2eV

K/2 ≥ 10.2

K ≥ 20.4 eV

விடை : 20.4eV 

2. போர் அணு மாதிரியில், நிலைமாற்றங்களின் (transitions) அதிர்வெண் பின்வரும் சமன்பாட்டினால் அறியப்படுகிறது. 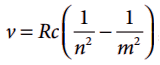, இங்கு n < m, பின்வரும் நிலை மாற்றங்களைக் கருதுக. 

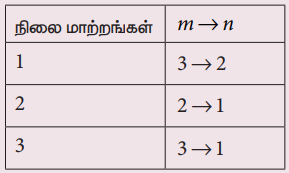
இந்நிலை மாற்றங்களின் அதிர்வெண் கூட்டல் விதிக்கு (இவ்விதி ரிட்ஸ் சேர்க்கைத் தத்துவம் என்றழைக்கப்படுகிறது) உட்படும் என்பதை நிறுவுக. 

தீர்வு: 

ரிட்ஸ் சேர்க்கைத்தத்துவம் (Ritz combination principle) நிலைமாற்றங்களின் அதிர்வெண் கூட்டல் விதிக்கு உட்படும். 

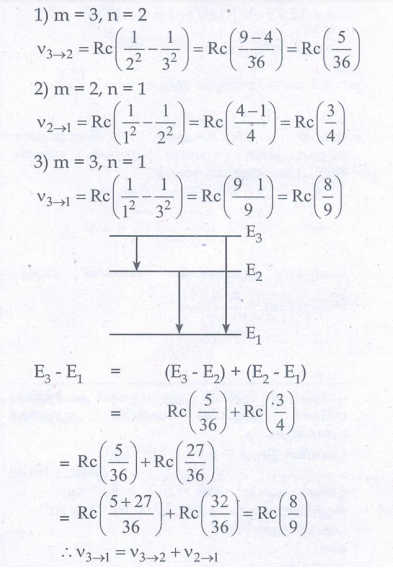
விடை: V3 → 2 + V 2 →1 = V3 → 1

3. அ) ஹைட்ரஜன் அணு ஒன்று அலைநீளம் 97.5 nm கொண்ட கதிர்வீச்சினால் கிளர்வுற செய்யப்படுகிறது. அக்கிளர்வு நிலையின் முதன்மைக் குவாண்டம் எண்ணைக் கணக்கிடுக. 

ஆ) வெளிவிடு நிறமாலையில் வரிகளின் மொத்த எண்ணிக்கை n(n–1) / 2 என்று காட்டுக. மேலும் கேள்வி (அ)-வில் கொடுக்கப்பட்டுள்ள கிளர்வு நிலையிலிருந்து கிடைக்கும் வெளிவிடு நிறமாலையில் சாத்தியமாகும் வரிகளின் எண்ணிக்கையைக் கணக்கிடுக.

தகவல் : λ = 97.5nm= 97.5 × 10−9 m = 975 × 10−10 m

தீர்வு :

ஆற்றல் E = hc / λ

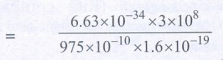
= 12.75 eV                [1eV = 1.6 × 10−19J]

En = −13.6/n2 eV

n = 1 எனில், அடிநிலை ஆற்றல் E1 = − (13.6 / l2)

E1 = −13.6 /n2 eV

ஆற்றல் மட்டங்களுக்கு இடையேயான வேறுபாட்டுக்குச் சமமான ஆற்றல் கொண்ட போட்டானை அணு உட்கவரும்

En = −13.6 + 12.75 = −0.85 eV

n2 = −13.6 / En = −13.6 / −0.85 = 16 n = 4 

வெளிவிடு நிறமாலையில் வரிகளின் மொத்த எண்ணிக்கை

= n (n-1) / 2 

= (4 × 3) / 2 

= 6

விடை : அ) n = 4 ஆ) ஆறு நிலைமாற்றங்கள் சாத்தியம் 

4. புவியின் அடர்த்தியும் அணுக்கருவின் அடர்த்தியும் ஒன்றாக இருப்பின் புவியின் ஆரத்தைக் கணக்கிடுக. (புவியின் நிறை = 5.97 × 1024 kg).

தகவல்: புவியின் நிறை = 5.97 × 1024 kg 

அணுக்கருவின் அடர்த்தி = 2.3 × 1017 kg/m3 

புவியின் ஆரம் R = ? 

தீர்வு :

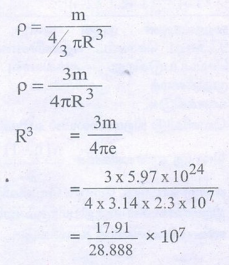
R3 = 0.62 × 107

R3 = 6.2 × 106

R = (6.2)1/3 × 102

= 1.84 × 102

R = 184m

விடை: 180m 

5. 47108Ag அணுக்கருவின் நிறை இழப்பு மற்றும் ஒரு நியூக்ளியானுக்கான பிணைப்பாற்றல் ஆகியவற்றைக் கணக்கிடவும் [47108Ag அணு நிறை Ag = 107.905949 u] 

தகவல் : 10847Ag அணுநிறை = 107.905949

தீர்வு:

BE = ∆mc2

∆m = [Zmp + Nmn − MA]

10847Ag அணுக்கருவில்

47 புரோட்டான்களையும் மற்றும்

61 நியூட்ரான்களையும் கொண்டு உள்ளது.

47 நியூட்ரான்களின் நிறை = 47 × 1.007825 u

= 47.367775 u

61 நியூட்ரான்களின் நிறை = 61 × 1.008665 u

= 61.528565 u

மொத்த நிறை = 47.367775 + 61.528565 

= 108.89634 u

நிறை இழப்பு ∆M = 108.89634 − 107.905949

∆M = 0.990391u

BE = 0.990391 u × c2

BE = 0.990391 × 931 MeV

BE/A = (0.990391 × 931) /108  MeV 

BE/A = = 8.5 MeVA

விடை:

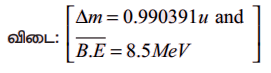
6. A மற்றும் B ஆகிய இரு கதிரியக்கத் தனிமங்களின் அரை ஆயுட்காலங்கள் முறையே 20 நிமிடங்கள் மற்றும் 40 நிமிடங்கள். தொடக்கத்தில் இவையிரண்டும் சம எண்ணிக்கையிலான அணுக்கருக்களைப் பெற்றுள்ளன எனில் 80 நிமிடங்களுக்குப்பிறகு A மற்றும் B ஆகியவற்றின் சிதைவடைந்த அணுக்கரு எண்ணிக்கைகளின் விகிதம் எவ்வளவு? 

விடை: 5 : 4 

7. அரை ஆயுட்காலம் 5.01 நாள்கள் கொண்ட சிறு அளவு 210Bi தனிமத்தின் செயல்பாட்டினை உன் பிறந்தநாளன்று அளவிடுகிறாய் என வைத்துக் கொள்வோம். தொடக்கத்தில் அதன் செயல்பாடு 1μCi 

அ) உன் அடுத்த பிறந்தநாளில் அதன் தோராயமான கதிரியக்கச் செயல்பாட்டு மதிப்பு எவ்வளவு? மேலும் 

ஆ) சிதைவு மாறிலி 

இ) சராசரி ஆயுள் மற்றும் 

ஈ) தொடக்கத்தில் இருந்த அணுக்களின் எண்ணிக்கை ஆகியவற்றைக் கணக்கிடுக. 

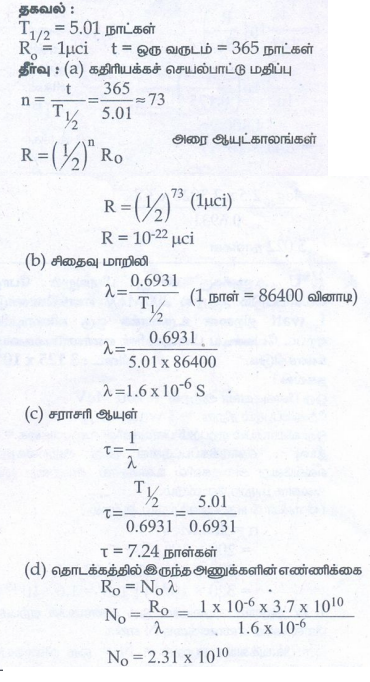
விடை: (அ) 10−22 μCi 

(ஆ) 1.6 × 10−6 s−1 

(இ) 7.24 நாட்கள் 

(ஈ) 2.31 × 1010 

8. ரேடான் உள்ள சிறு அளவு கதிரியக்கப் பொருள் 60% சிதைவடைய ஆகும் காலத்தைக் கணக்கிடுக. (ரேடானின் T1/2 = 3.8 நாள்கள்)

தகவல்: 

ரேடானின் அரை ஆயுட்காலம் = 3.8 நாள்கள் 

சிதைவடையும் பொருளின் அளவு = 60% 

எடுத்துக்கொள்ளும் காலம் =? 

தீர்வு

λ = 0.6931/3.8 நாள் சிதைவடையும் அளவு = 60%

எஞ்சியிருக்கும் அளவு = 40%

தொடக்கத்தில் உள்ள அளவு No என்க 

கதிரியக்கச்சிதைவு விதியின்படி, N = No e −λt 

N = No ல் N = 40% எனில்

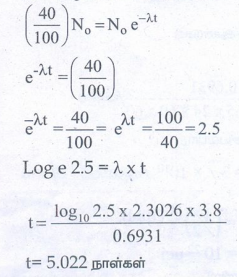
t = 5.022 நாள்கள்

விடை: 5.022 நாள்கள் 

9. 23592U அணுக்கரு ஒன்று பிளவுறும் போது வெளிப்படும் ஆற்றல் 200 MeV எனக்கொண்டு, 1 watt திறனை உருவாக்க ஒரு வினாடியில் ஏற்பட வேண்டிய பிளவுகளின் எண்ணிக்கையைக் கணக்கிடுக.

தகவல்: 

ஒரு பிளவுக்கான ஆற்றல் = 200 MeV 

தேவைப்படும் திறன் =1 watt =1J/s 

ஒரு வினாடியில் ஏற்படும் பிளவுகளின் எண்ணிக்கை =? 

தீர்வு: 

கொடுக்கப்பட்டுள்ள இரு ஆற்றல்களும் வெவ்வேறு அலகுகளில் உள்ளதால், அவற்றை ஒரே அலகாக மாற்ற வேண்டும். 

1 பிளவின் போது வெளிப்படும் ஆற்றல்

n = 200 MeV 

= 200 × 106 eV

= 200 × 106 × 1.6 × 10−19 J.

= 320 × 10−13 J              [1eV = 1.6 ×10−19 J]

1 W திறனை உருவாக்க, ஒரு வினாடியில் ஏற்படும் பிளவுகளின் எண்ணிக்கை N என்க. 

ஒரு பிளவுக்கான ஆற்றல் × N = ஒரு வினாடியில் வெளிப்படும் மொத்த ஆற்றல் 

= 320 × 10−13 × N = 1J/S

N = 1 / [320 × 10−13]  = 3.125 × 1010 பிளவுகள்

1 watt திறனை உருவாக்க, ஒரு வினாடியில் ஏற்படும் பிளவுகளின் எண்ணிக்கை 3.125 × 1010 ஆகும்

விடை: 3.125 × 1010 

10. கதிரியக்கச் செயல்பாடு 1 Ci என்றிருக்கும் ரேடியத்தின் (22688Ra) நிறை ஏறக்குறைய 1g எனக் காட்டுக. (T1/2 = 1600 ஆண்டுகள்) 

தகவல்: 

T1/2 =1600 ஆண்டுகள் 

1 கியூரி = 3.7 × 1010 சிதைவுகள்/வினாடி 

ரேடியத்தின் அளவு = ? 

தீர்வு:

11. தொல்வியல் பகுதி (archaeological site) ஒன்றிலிருந்து மரத்தின் கரித்துண்டுகள் கிடைக்கின்றன. தற்போது உயிருடன் உள்ள மரத்திலிருந்து பெறப்பட்ட சிறுபகுதியிலுள்ள கார்பன்−14 ன் அளவைப் போல் இக்கரியிலுள்ள அதேயளவு மாதிரியில் காணப்படும் கார்பன்−14 ன் அளவு 17.5% மட்டுமே உள்ளது எனில் அம்மரத்தின் வயது என்ன?

விடை: 1.44 × 104 வருடம்