பயிற்சி 3.2

பயிற்சி 3.2

பல்வகைத் திறனறிப் பயிற்சிக் கணக்குகள்

1. ஒரு துண்டுக் கம்பியின் நீளம் 36 செ.மீ. அக்கம்பியைக் கீழ்க்காணும் வடிவங்களாக உருவாக்கினால் ஒவ்வொரு பக்கத்தின் நீளம் என்னவாக இருக்கும்?

i) ஒரு சதுரம்

ii) ஒரு சமபக்க முக்கோணம்

விடை :1) 9 செ.மீ. ii) 12 செ.மீ.

2. 40 செ.மீ பக்க அளவுள்ள ஒரு சமபக்க முக்கோணத்தின் ஒரு முனையிலிருந்து 6 செ.மீ பக்கமுள்ள ஒரு சமபக்க முக்கோணம் நீக்கப்படுகிறது எனில் மீதியுள்ள பகுதியின் சுற்றளவு என்ன?

விடை :

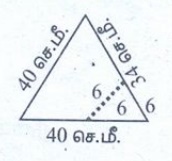
மீதமுள்ள பகுதியின் சுற்றளவு = (40 + 34 + 6 + 34) செ.மீ.

= 114 செ.மீ.

3. இரஹீம் மற்றும் பீட்டர் இருவரும் காலை நடைப்பயிற்சிக்குச் செல்கின்றனர். இரஹீம் 50 மீட்டர் பக்கமுள்ள ஒரு சதுர வடிவ நடைபாதையிலும், பீட்டர் 40 மீ நீளம் மற்றும் 30 மீ அகலம் உள்ள செவ்வக வடிவ நடைபாதையிலும் நடக்கின்றனர். அவர்கள் ஒவ்வொருவரும் 2 சுற்றுகள் நடந்திருந்தால் அதிகமான தொலைவு நடந்துள்ளவர் யார்? எவ்வளவு தொலைவு அதிகமாக நடந்துள்ளார்?

விடை :

ரஹீம் கடந்த தொலைவு = 50மீ × 4 = 200மீ 

2 சுற்றுகள் நடந்திருந்தால், கடந்த தொலைவு = 2 × 200மீ = 400மீ 

பீட்டர் கடந்த தொலைவு = 2 (40 + 30) மீ

= 2 (70) மீ = 140 மீ 

2 சுற்றுகள் நடந்திருந்தால், கடந்த தொலைவு

= 2 × 140 மீ = 280 மீ

அதிகமாக நடந்துள்ள தொலைவு

(400 – 280) = 120 மீ

4. ஒரு செவ்வக வடிவப் பூங்காவின் நீளம் அகலத்தைவிட 14 மீ அதிகமாக உள்ளது. அப்பூங்காவின் சுற்றளவு 200 மீ எனில் அதன் நீளம் மற்றும் பரப்பளவு காண்க.

விடை : 

அகலத்தை b + 14 மீ என்க. 

அகலம் = b 

சுற்றளவு = 200

2 (l + b) = 200 

2 (b + 14 + b) = 200

2 (2b + 14) = 200

28 + 4 b = 200

4 b = 200 – 28 

4 b = 172 மீ

b = 172/4

b = 43 மீ 

நீளம் = b + 14

= 43 + 14 

நீளம் l = 57 மீ 

பரப்பளவு = l × b ச. அலகுகள்

= 57 × 43 மீ2

= 2451 மீ2

5. உன்னுடைய தோட்டம் 5 மீ பக்க அளவுடைய சதுர வடிவில் உள்ளது. ஒவ்வொரு பக்கமும் 2 சுற்றுகள் கம்பியால் வேலி அமைக்க வேண்டும். மீட்டருக்கு ₹10 வீதம் தோட்டத்திற்கு வேலி அமைக்கத் தேவைப்படும் தொகையினைக் காண்க.

விடை :

a = 5 மீ

தோட்டத்தின் சுற்றளவு = 4a அலகுகள் 

= 4 × 5 மீ = 20 மீ

ஒரு சுற்றுக்கு 1 மீட்டருக்கு வேலி அமைக்க ஆகும் செலவு = ₹. 10 

20 மீட்டருக்கு வேலி அமைக்க ஆகும் செலவு = ₹. 10 × 20

= ₹. 200 

2 சுற்றுகளுக்கு வேலி அமைக்க தேவைப்படும் தொகை

= 2 × ₹. 200 

= ₹. 400

மேற்சிந்தனைக் கணக்குகள்

6. 20 சமபக்கங்கள் கொண்ட வடிவத்தின் ஒரு பக்க அளவு 3 செ.மீ எனில் அதன் சுற்றளவு காண்க. 

விடை : 60 செ.மீ. 

7. ஒரு செவ்வகத்தின் நீளம் 40 செ.மீ மற்றும் அகலம் 20 செ.மீ எனில் அச்செவ்வகத்திலிருந்து எத்தனை 10 செ.மீ பக்க அளவுள்ள சதுரங்களை உருவாக்க முடியும்?

விடை :

l = 40 செ.மீ. , b = 20 செ.மீ. 

செவ்வகத்தின் பரப்பளவு = l × b சதுர அலகுகள்

= 40 × 20 செ.மீ.2

= 800 செ.மீ. 2

a = 10 செ.மீ. 

சதுரத்தின் பரப்பளவு = a × a சதுர அலகுகள் 

= 10 × 10 செ.மீ. 2  

= 100 செ.மீ. 2

உருவாக்கப்பட்ட சதுரங்கள் = 800/100 செ.மீ. 2

= 8

8. ஒரு செவ்வகத்தின் நீளமானது அதன் அகலத்தைப் போல் மூன்று மடங்காகும். அதன் சுற்றளவு 64 செ.மீ எனில் செவ்வகத்தின் பக்கங்களைக் காண்க.

விடை : 

நீளம் l = 3b

அகலம் = b

சுற்றளவு  = 64 செ.மீ.

2 (l + b) = 64 செ.மீ. 

 2 (3b + b) = 64

2 (4b) = 64

8 b = 64

b = 64/8

அகலம் b = 8 செ.மீ. 

நீளம் l = 3b

l = 3 × 8

= 24 செ.மீ.

9. 48 செ.மீ நீளமுள்ள ஒரு கம்பியைக் கொண்டு எத்தனை வெவ்வேறு செவ்வகங்களை உருவாக்க முடியும்? அச்செவ்வகங்களின் சாத்தியமான நீளம் மற்றும் அகலம் காண்க.

விடை :

12 செவ்வகங்கள் 

(1,23), (2, 22), (3,21), (4, 20), (5, 19), (6, 18),(7, 17),(8, 16),(9, 15),(10, 14), (11,13), (12, 12) 

10. சதுரம் A இன் பக்கங்களைப் போன்று இரண்டு மடங்கு பக்கங்கள் கொண்ட சதுரம் B ஐ வரைக. A மற்றும் B இன் சுற்றளவுகளைக் காண்க.

விடை : 

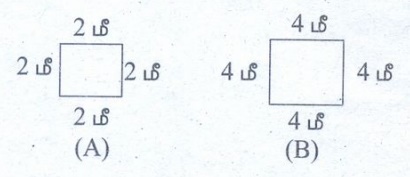
சதுரம் B இன் சுற்றளவு = 4 × 4 மீ.

= 16 மீ. 

சதுரம் A இன் சுற்றளவு = 4 × 2 மீ.

= 8 மீ. 

சதுரம் B இன் சுற்றளவானது, சதுரம் A இன் சுற்றளவை போல் இருமடங்கு.

11. ஒரு சதுரத்தின் பக்கத்தை நான்கில் ஒரு பங்காகக் குறைத்தால் உருவாகும் புதிய சதுரத்தின் பரப்பளவில் என்ன மாற்றம் ஏற்படும்?

விடை : 

புதிய சதுரத்தின் பரப்பளவானது அசல் பரப்பளவிலிருந்து 1/16 முறை குறைக்கப்பட்டது. 

12. இரண்டு வீட்டு மனைகள் ஒரே சுற்றளவைப் பெற்றுள்ளன. அதில் ஒன்று 10 மீ பக்கம் கொண்ட சதுர வடிவமாகும். மற்றொன்று 8 மீ அகலம் கொண்ட செவ்வக வடிவமாகும் எனில் எந்த வீட்டு மனை அதிகப் பரப்பளவு பெற்றுள்ளது? எவ்வளவு அதிகம் ?

விடை :

a = 10 மீ., b = 8 மீ. 

சதுர வடிவ மனையின் சுற்றளவு = 4 a அலகுகள்

= 4 × 10 மீ.

= 40 மீ. 

செவ்வக வடிவ மனையின் சுற்றளவு

40 = 2 (l + b) அலகுகள் 

40 = 2 (l + 8) மீ.

40 = 2 l + 16 

2 l = 40 – 16 

2 l  = 24

 l  = 24/2

l = 12 மீ. 

சதுர வடிவ மனையின் பரப்பளவு

= a × a சதுர அலகுகள்

= 10 × 10 மீ.2

= 100 மீ. 2

செவ்வக வடிவ மனையின் பரப்பளவு

= l × b சதுர அலகுகள் 

= 8 × 12 மீ.2

= 96 மீ.2 

அதிகமான பரப்பளவு 100மீ.2 – 96 மீ2 = 4 மீ2

13. கொடுக்கப்பட்ட வீட்டின் படத்தை உற்றுநோக்கி நிழலிடப்பட்ட பகுதியின் மொத்தப் பரப்பளவைக் காண்க.

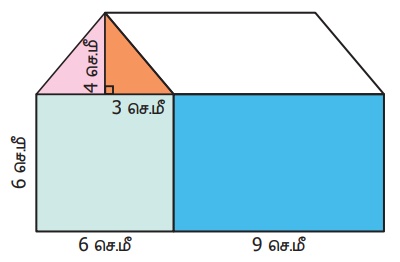
விடை :

சதுரத்தின் பரப்பளவு = a × a சதுர அலகுகள்

= 6 × 6 செ.மீ.2

= 36 செ.மீ. 2

செவ்வகத்தின் பரப்பளவு = l × b சதுர அலகுகள்

= 9 × 6 செ.மீ. 2

= 54 செ.மீ. 2

முக்கோணத்தின் பரப்பளவு

= ½  ×  b × h ச.அ

=  ½ ×  4 × 6 செ.மீ. 2

= 12 செ.மீ. 2

 நிழலிடப்பட்ட பகுதியின் மொத்தப்பரப்பளவு

= (36 + 54 + 12) செ.மீ. 2 

= 102 செ.மீ. 2

14. சதுரக் கட்டத்தில் கொடுக்கப்பட்ட மலரின் தோராய பரப்பளவைக் காண்க.

விடை :

முழு சதுரங்கள் = 11

அரை சதுரங்கள் = 9

11 முழு சதுரங்களின் பரப்பளவு = 11 × 1 செ.மீ. 2

= 11 செ.மீ. 2

9 அரை சதுரங்களின் பரப்பளவு

= 9 × ½ செ.மீ. 2

= 4.5 செ.மீ. 2

மலரின் தோராய பரப்பளவு = (11 + 4.5) செ.மீ. 2

= 15.5 செ.மீ. 2