கூட்டு வடிவங்களின் சுற்றளவு மற்றும் பரப்பளவு

கூட்டு வடிவங்களின் சுற்றளவு மற்றும் பரப்பளவு

பல்வேறு மூடிய வடிவங்களின் தொகுப்பே ஒரு கூட்டு வடிவம் ஆகும். அவ்வடிவத்தின் ஒட்டு மொத்த வெளிப்பக்க அளவுகளின் (எல்லைகள்) கூட்டுத் தொகையே அதன் சுற்றளவு எனக் கணக்கிடப்படுகிறது. அனைத்து மூடிய வடிவங்களின் பரப்பளவுகளின் கூட்டுத் தொகையானது அக்கூட்டு வடிவத்தின் பரப்பளவாகக் கணக்கிடப்படுகிறது.

எடுத்துக்காட்டு 12

கொடுக்கப்பட்ட வடிவத்தின் சுற்றளவு காண்க.

தீர்வு

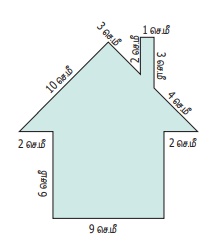
சுற்றளவு = மொத்த எல்லையின் நீளம்

= (6 + 2 + 10 + 3 + 2 + 1 + 3 + 4 + 2 + 6 + 9) செ.மீ.

 = 48 செ.மீ.

எடுத்துக்காட்டு 13

பின்வரும் 'L' வடிவ அட்டையின் சுற்றளவு மற்றும் பரப்பளவு காண்க.

தீர்வு

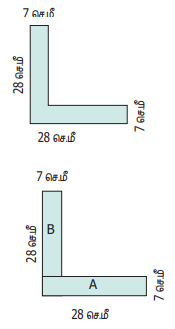
சுற்றளவு = (28 + 7 + 21+ 21 + 7 + 28) செ.மீ.

 = 112 செ.மீ.

'L' வடிவ அட்டையின் பரப்பளவு காண, அது

இரண்டு செவ்வகங்களாக A மற்றும் B எனப் பிரிக்கப்படுகிறது.

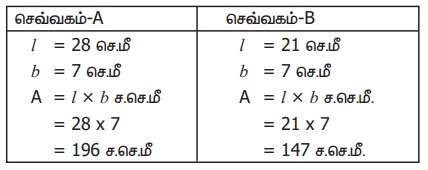
'L' வடிவ அட்டையின் பரப்பளவு = (196 + 147) ச.செ.மீ. 

= 343 ச.செ.மீ.

செயல்பாடு 

இரு செவ்வகங்களைக் கொண்டு அமையும் 'L' வடிவ அட்டையினைச் சம அளவு சதுரங்களாகப் பிரித்து பரப்பளவைக் காண்க.

சிந்திக்க

'L' வடிவ அட்டையின் பரப்பளவை இரண்டு பரப்பளவுகளின் வேறுபாடாகக் காண இயலுமா?

இவற்றை முயல்க

அளவுகோலால் அளந்து பின்வரும் உருவங்களுக்குச் சுற்றளவு காண்க.

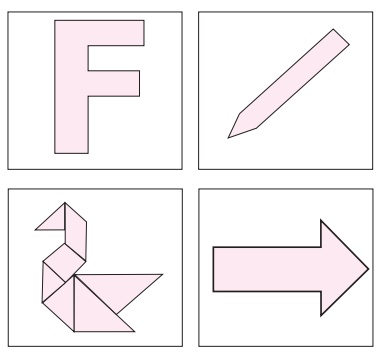
செயல்பாடு

ஒவ்வொன்றும் 4 செ.மீ பக்க அளவுள்ள 9 சதுரங்களைக் கொண்டு 80 செ.மீ சுற்றளவு கொண்ட அனைத்து சாத்தியமான வடிவங்களையும் உருவாக்குக.

1. கொடுக்கப்பட்ட வடிவத்திலிருந்து ஒரு குறிப்பிட்ட பகுதியை நீக்குதலின் / சேர்த்தலின் தாக்கம்

8 செ.மீ அகலமும் 12 செ.மீ நீளமும் கொண்ட ஒரு செவ்வகத்தைக் கருதுக.

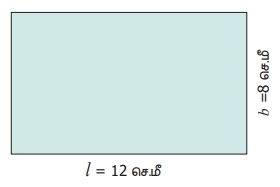
நீளம், l = 12 செ.மீ; அகலம் b = 8 செ.மீ.

பரப்பளவு, A  = (l × b) சதுர அலகுகள்.

 = 12 × 8

= 96 சதுர செ.மீ.

சுற்றளவு, P = 2 (l + b) சதுர அலகுகள்.

 = 2 (12+8)

 = 40 செ.மீ.

பின்வரும் சூழல்களில் செவ்வகத்தின் சுற்றளவு மற்றும் பரப்பளவு இவற்றில் ஏற்படும் மாற்றங்களை உற்று நோக்குக.

சூழல் 1

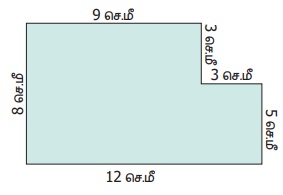
செவ்வகத்தின் ஒரு மூலையில் 3 செ.மீ பக்க அளவுள்ள ஒரு சதுரம் வெட்டப்பட்டால் அதன் பரப்பளவு, A = ( l × b) – (S × S) சதுர அலகுகள்

= (12 × 8) – (3 × 3)

= 87 சதுர செ.மீ.

சுற்றளவு, P = (மொத்த எல்லைகள்) அலகுகள்

 = 8 + 12 + 5 + 3 + 3 + 9 = 40 செ.மீ.

சுற்றளவு மாறவில்லை. ஆனால் பரப்பளவு குறைகிறது.

சூழல் 2

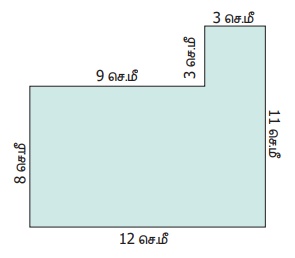
3 செ.மீ பக்க அளவுள்ள ஒரு சதுரம் செவ்வகத்தோடு இணைக்கப்படுகிறது எனில் அதன்

பரப்பளவு, A = (l ×  b) + ( S × S) சதுர அலகுகள்.

= (12 × 8) + (3 × 3)

= 105 சதுர செ.மீ.

சுற்றளவு, P = (மொத்த எல்லைகள்) அலகுகள்.

 = 8 + 12 + 11 + 3 + 3 + 9 = 46 செ.மீ.

இங்கு, சுற்றளவு மற்றும் பரப்பளவு இரண்டுமே அதிகரிக்கின்றன.

எடுத்துக்காட்டு 14 

15 செ.மீ பக்க அளவுடைய நான்கு சதுர தரை விரிப்புகள் இணைக்கப்பட்டு ஒரு செவ்வக விரிப்போ அல்லது ஒரு சதுர விரிப்போ உருவாக்கலாம் எனில் எந்தத் தரை விரிப்பு அதிகமான பரப்பளவு மற்றும் நீண்ட சுற்றளவு பெற்றிருக்கும்?

தீர்வு 

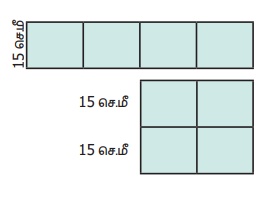
செவ்வகத்தின் சுற்றளவு, P = 2 (l + b) அலகுகள்.

 = 2 (60 + 15) = 150 செ.மீ.

செவ்வகத்தின் பரப்பளவு, A = (l × b) சதுர அலகுகள்.

 = 60 × 15 = 900 சதுர செ.மீ

சதுரத்தின் சுற்றளவு, P = (4 × S) அலகுகள்.

 = (4 × 30) = 120 செ.மீ.

சதுரத்தின் பரப்பளவு, A = (S × S) சதுர அலகுகள்.

 = 30 × 30 = 900 சதுர செ.மீ

பரப்பளவுகளில் எந்த மாற்றமும் இல்லை. ஆனால், செவ்வக வடிவத் தரை விரிப்பு அதிகச் சுற்றளவைப் பெற்றுள்ளது.

செயல்பாடு

ஒரு செவ்வக வடிவத் தாளை அதன் மூலைவிட்டத்தின் வழியே வெட்டவும். இரண்டு சர்வ சம அசமபக்க செங்கோண முக்கோணங்கள் கிடைக்கின்றன. அவற்றின் ஒத்த பக்கங்களைப் பின்வருமாறு இணைத்தால் ஆறு வடிவங்களைப் பெற முடியும். அவற்றுள் நான்கு வடிவங்கள் கொடுக்கப்பட்டுள்ளன. மற்ற இரண்டு வடிவங்களைக் காண்க. மேலும் ஆறு வடிவங்களின் சுற்றளவுகளையும் கண்டறிந்து அவற்றை அட்டவணைப்படுத்துக.

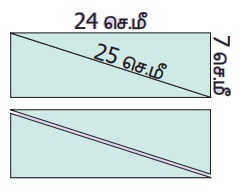
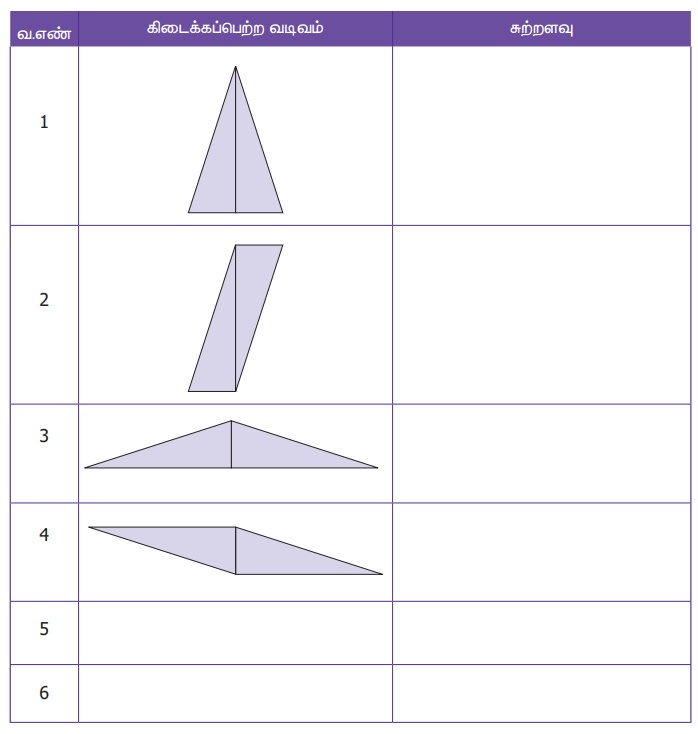
மேலே உள்ள செயல்பாடுகளின் அடிப்படையில், கீழே உள்ள வினாக்களுக்கு விடையளிக்கவும்.

i) அனைத்து வடிவங்களும் ஒரே சுற்றளவைப் பெற்றுள்ளனவா?

ii) எந்த வடிவம் அதிக பட்ச சுற்றளவைப் பெற்றுள்ளது?

iii) எந்த வடிவம் குறைந்த பட்ச சுற்றளவைப் பெற்றுள்ளது? 

iv) அனைத்து வடிவங்களின் பரப்பளவுகள் சமமா? ஏன்?

உங்களுக்குத் தெரியுமா?

• ஒரே சுற்றளவு கொண்ட வடிவங்கள் வெவ்வேறு பரப்பளவுகளைப் பெற்றிருக்கலாம்.

• ஒரே பரப்பளவு கொண்ட வடிவங்கள் வெவ்வேறு சுற்றளவுகளைப் பெற்றிருக்கலாம்.