சுற்றளவு

சுற்றளவு

செயல்பாடு

பின்வரும் வடிவங்களை உற்றுநோக்கிக் கீழே கொடுக்கப்பட்ட வினாக்களுக்கு விடையளிக்கவும்.

i) மூடிய வடிவங்களை (✔) எனவும் மூடப்படாத வடிவங்களை (X) எனவும் குறிக்கவும். 

ii) அளவுகோலைப் பயன்படுத்தி மூடிய வடிவங்களின் எல்லையை அளக்கவும்.

iii) எந்த மூடிய வடிவம் மிகக்குறைந்த எல்லையைப் பெற்றுள்ளது? முதல் வடிவம்

iv) எந்த மூடிய வடிவம் மிக அதிகமான எல்லையைப் பெற்றுள்ளது? ப வடிவம்

ஒரு மூடிய வடிவத்தின் எல்லையின் நீளம் அவ்வடிவத்தின் சுற்றளவு எனப்படும். எனவே, சுற்றளவு என்பது ஒரு மூடிய வடிவத்தைச் 'சுற்றியுள்ள அளவு' ஆகும். சுற்றளவின் அலகானது நீளத்தின் அலகே ஆகும். மீட்டர், மில்லி மீட்டர், சென்டி மீட்டர், கிலோ மீட்டர், அங்குலம், அடி, கெஜம் (yard) போன்ற அலகுகளால் சுற்றளவு குறிக்கப்படுகிறது.

உங்களுக்குத் தெரியுமா?

சுற்றளவு (Perimeter) என்ற சொல்லானது கிரேக்கச் சொற்களான 'peri' மற்றும் 'metron' என்ற சொற்களிலிருந்து பெறப்பட்டது. இங்கு 'peri' என்பது 'சுற்றிலும்' எனவும் 'metron' என்பது 'அளவு' எனவும் பொருள் கொள்ளப்படுகின்றன.

1. செவ்வகத்தின் சுற்றளவு

செவ்வகத்தின் சுற்றளவு = செவ்வகத்தின் மொத்த எல்லையின் நீளம்

= நீளம் + அகலம் + நீளம் + அகலம்

= 2 நீளம் + 2 அகலம்

= 2 (நீளம் + அகலம்)

ஒரு செவ்வகத்தின் நீளம், அகலம் மற்றும் சுற்றளவு ஆகியவற்றை முறையே l, b மற்றும் P எனக் குறிப்போம். எனவே, செவ்வகத்தின் சுற்றளவு, P = 2 (l + b) அலகுகள்

குறிப்பு

ஒரு செவ்வகத்தின் எதிரெதிர் பக்கங்கள் சம நீளமுடையவை.

உங்களுக்குத் தெரியுமா?

படத்தில் PQRS என்பது நடைபாதையின் வெளிப்புற எல்லையையும் ABCD என்பது நடைபாதையின் உட்புற எல்லையையும் குறிக்கிறது.

எடுத்துக்காட்டு 1 ஒரு சதுரத்தின் நீளம் 12 செ.மீ. மற்றும் அகலம் 10 செ.மீ. எனில் அதன் சுற்றளவு காண்க.

தீர்வு

l = 12 செ.மீ

b = 10 செ.மீ

செவ்வகத்தின் சுற்றளவு, P = 2 (l + b) அலகுகள்

= 2 (12 + 10)

= 2 × 22

= 44 செ.மீ

ஆகவே, செவ்வகத்தின் சுற்றளவு 44 செ.மீ ஆகும்.

2. சதுரத்தின் சுற்றளவு

சதுரத்தின் சுற்றளவு = சதுரத்தின் மொத்த எல்லையின் நீளம்

= பக்கம் + பக்கம் + பக்கம் + பக்கம்

= (4 × பக்கம்) அலகுகள்

சதுரத்தின் ஒரு பக்கம் 'S' எனில் சதுரத்தின் சுற்றளவு, P = 4 × S அலகுகள் = 4S அலகுகள்

குறிப்பு

● ஒரு சதுரத்தின் அனைத்துப் பக்கங்களும் சம நீளமுடையவை.

● பல பக்கங்களைக் கொண்ட ஒரு ஒழுங்கு பலகோணத்தின்

சுற்றளவு = பக்கங்களின் எண்ணிக்கை × ஒரு பக்கத்தின் நீளம்.

எடுத்துக்காட்டு 2: ஒரு சதுரத்தின் பக்கம் 5 செ.மீ. எனில், அதன் சுற்றளவு காண்க.

தீர்வு

S = 5 செ.மீ

சதுரத்தின் சுற்றளவு, P = (4 × S) அலகுகள்

= 4 × 5

= 20 செ.மீ

சதுரத்தின் சுற்றளவு 20 செ.மீ ஆகும்.

3. முக்கோணத்தின் சுற்றளவு

முக்கோணத்தின் சுற்றளவு = முக்கோணத்தின் மொத்த எல்லையின் நீளம்

= பக்கம் 1 + பக்கம் 2 + பக்கம் 3

ஒரு முக்கோணத்தின் மூன்று பக்கங்களை a, b மற்றும் c எனக் கொண்டால், அதன் சுற்றளவு, P = (a + b + c) அலகுகள்.

எடுத்துக்காட்டு 3: 3 செ.மீ, 4 செ.மீ மற்றும் 5 செ.மீ பக்க அளவுகள் கொண்ட ஒரு முக்கோணத்தின் சுற்றளவு காண்க.

தீர்வு

a = 3 செ.மீ

b = 4 செ.மீ

c = 5 செ.மீ

முக்கோணத்தின் சுற்றளவு, P = (a + b + c) அலகுகள்

= 3 + 4 + 5 = 12 செ.மீ 

முக்கோணத்தின் சுற்றளவு 12 செ.மீ ஆகும்.

சிந்திக்க

கொடுக்கப்பட்ட வடிவத்திற்கு சுற்றளவு கண்டறிய இயலுமா? ஏன் ?

இல்லை இயயாது. ஏனெனில் மூடப்படவில்லை.

இவற்றை முயல்க

i) ஒரு புள்ளித் தாளில் 16 செ.மீ சுற்றளவு கொண்ட ஒரு வடிவம் வரைக.

ii) ஒரு செவ்வகத்தின் நீளமானது அதன் அகலத்தைப் போல் இரண்டு மடங்கு எனில் அதன் சுற்றளவு என்ன?

x + 2x + x + 2x = 6x

iii) ஒரு சதுரத்தின் பக்கம் பாதியாக்கப்பட்டால் கிடைக்கப்பெற்ற சதுரத்தின் சுற்றளவு என்ன? 

சுற்றளவு பாதியாகும்

iv) ஒரு முக்கோணத்தின் அனைத்துப் பக்கங்களும் சம நீளமுடையவை எனில் அதன் சுற்றளவு என்ன? 

 x + x + x = 3x

செயல்பாடு

வகுப்பறையில் உள்ள மேசை, A4 தாள், குறிப்பேடு போன்ற எவையேனும் ஐந்து பொருள்களைத் தேர்ந்தெடுக்கவும். அவற்றின் பக்க அளவுகளைத் தோராயமாகக் கணக்கிட்டு ஒவ்வொன்றின் சுற்றளவையும் மதிப்பீடு செய்க. பின்னர் அளவுகோல் கொண்டு உண்மையான சுற்றளவை அளந்து பின்வரும் அட்டவணையை நிரப்பி வித்தியாசத்தை செ.மீ. இக்குத் திருத்தமாகக் காண்க. 

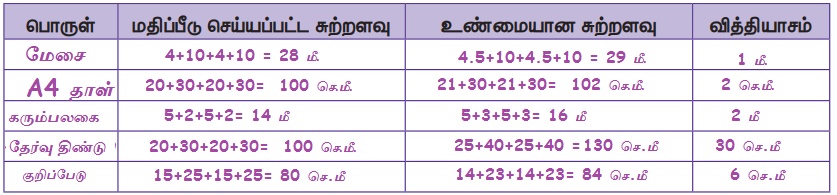
எடுத்துக்காட்டு 4: ஒரு கரும்பலகையின் சுற்றளவு 6 மீ மற்றும் அகலம் 1 மீ எனில் நீளத்தைக் காண்க.

தீர்வு

கரும்பலகையின் சுற்றளவு, P = 6 மீ

கரும்பலகையின் அகலம், b = 1 மீ

நீளம், l =?

2 (l + b) = 6 

2 (l +1) = 6

l + 1 = 6/2

     = 3

 l  = 3 – 1

= 2 மீ

கரும்பலகையின் நீளம் 2 மீ ஆகும்.

எடுத்துக்காட்டு 5: ஒரு சதுர வடிவமான தபால் வில்லையின் சுற்றளவு 8 செ.மீ எனில் அதன் பக்க அளவைக் காண்க.

தீர்வு

சதுரத்தின் சுற்றளவு, P = 8 செ.மீ

4 × S = 8

S = 8/4 = 2 செ.மீ

தபால் வில்லையின் பக்க அளவு 2 செ.மீ ஆகும்.

எடுத்துக்காட்டு 6: ஒரு சமபக்க முக்கோணத்தின் சுற்றளவு 129 செ.மீ எனில் அதன் ஒரு பக்கஅளவைக் காண்க. 

தீர்வு

சமபக்க முக்கோணத்தின் சுற்றளவு, P = 129 செ.மீ

 a + a + a = 129

3 × a = 129

a = 129/3

= 43 செ.மீ

சமபக்க முக்கோணத்தின் ஒரு பக்க அளவு 43 செ.மீ ஆகும்.

எடுத்துக்காட்டு 7 

தென்றல், தாரணி மற்றும் தனம் ஆகியோருக்கு முறையே 12 செ.மீ நீளமுள்ள நூல் துண்டுகள் வழங்கப்படுகின்றன. இந்த நூலினைக் கொண்டு செவ்வகம், சதுரம் மற்றும் முக்கோணம் ஆகியவற்றை உருவாக்குமாறு அவர்கள் கேட்டுக் கொள்ளப்படுகிறார்கள். இது ஒரு கணிதச் செயல்பாடு ஆகும். அவர்கள் ஒவ்வொருவரும் எத்தனை வடிவங்களை உருவாக்க முடியும் ?

தீர்வு

தென்றல்

செவ்வகத்தின் சுற்றளவு, P = 12 செ.மீ

2 (l + b) = 12

l + b = 12/2

= 6 செ.மீ

கூட்டுத்தொகை 6–ஐத் தரக்கூடிய சோடி அளவுகள் (5, 1) மற்றும் (4, 2) ஆகும். எனவே, இரு வழிகளில் செவ்வகத்தை உருவாக்க முடியும். 5 செ.மீ நீளமும் 1 செ.மீ அகலமும் கொண்ட ஒரு செவ்வகத்தையும், 4 செ.மீ நீளமும் 2 செ.மீ அகலமும் கொண்ட மற்றொரு செவ்வகத்தையும் தென்றலால் உருவாக்க முடியும்.

தாரணி

சதுரத்தின் சுற்றளவு, P = 12 செ.மீ

4 × S = 12

S = 12/ 4

   = 3 செ.மீ

எனவே, 3 செ.மீ பக்கமுள்ள ஒரே ஒரு சதுரத்தை மட்டுமே தாரணியால் உருவாக்க முடியும். 

தனம்

முக்கோணத்தின் சுற்றளவு, P = 12 செ.மீ

a + b + c = 12 செ.மீ

கூட்டுத்தொகை 12–ஐத் தரக்கூடியதும் முக்கோணச் சமனின்மை விதியை நிறைவு செய்வதுமான மூன்றன் தொகுதி அளவுகள் (2, 5, 5) ; (3, 4, 5) ; (4, 4, 4) ஆகும். எனவே தனத்தால், 2 செ.மீ, 5 செ.மீ & 5 செ.மீ; 3 செ.மீ, 4 செ.மீ & 5 செ.மீ மற்றும் 4 செ.மீ, 4 செ.மீ & 4 செ.மீ ஆகியவற்றைப் பக்க அளவுகளாக உடைய 3 முக்கோணங்களை உருவாக்க முடியும்.

சிந்திக்க: வெவ்வேறு வடிவங்கள் ஒரே சுற்றளவைப் பெற்றிருக்க முடியுமா?

எடுத்துக்காட்டு 8

12 மீ பக்க அளவுடைய ஒரு சதுர வடிவிலான வீட்டு மனைக்கு வேலி அமைக்க மீட்டருக்கு  ₹15/– வீதம் ஆகும் செலவைக் காண்க.

தீர்வு

சதுர வடிவிலான வீட்டு மனையின் ஒரு பக்கம் = 12 மீ

சதுர வடிவிலான வீட்டு மனையின் சுற்றளவு = (4 × S) அலகுகள்

= 4 × 12 = 48 மீ

மீட்டருக்கு   ₹15/– வீதம் மனைக்கு வேலி அமைக்க ஆகும் தொகை = 48 × 15 = ₹720

இவற்றை முயல்க

i) ஒரு செவ்வகத்தின் சுற்றளவு 14 மீ. அதன் நீளம் 4 மீ. எனில் அதன் அகலம் காண்க.

விடை: 

2 (l + b) = S 

2(4+b) = S 

b = (14−8)/2 = 3மீ

ii) ஓர் இரு சமபக்க முக்கோணத்தின் சுற்றளவு 21 செ.மீ மூன்றாவது பக்கம் 5 செ.மீ எனில் சம பக்கங்களின் அளவுகள் காண்க.

விடை: 

a + b + c  = S 

5 + b + b  = 21 

b = (21−5)/2= 8 செ.மீ