வெக்டர்களின் வடிவக்கணித அறிமுகம் (Geometric introduction to vectors)

வெக்டர்களின் வடிவக்கணித அறிமுகம் (Geometric introduction to vectors)

முப்பரிமாணவெளி ℝ3−ல் என்ற வெக்டர், A = (a1,a2,a3) ∈ ℝ3 என்ற புள்ளியை ஒரு தொடக்கப் புள்ளியாகவும் B = (b1,b2,b3) ∈ ℝ3 என்ற முடிவுப் புள்ளியாகவும் கொண்ட ஒரு திசையிடப்பட்ட கோட்டுத்துண்டால் குறிப்பிடப்படுகிறது. இதனை எனக் குறிக்கிறோம். AB என்ற கோட்டுத்துண்டின் நீளம் என்ற வெக்டரின் எண்ணளவாகும், மற்றும் A−இல் இருந்து B−ன் திசையானது என்ற வெக்டரின் திசையாகும். எனவே, ஒரு வெக்டரை அல்லது எனக் குறிப்பிடலாம். ℝ3  −ல் -ன் நீளம்   -ன் நீளத்திற்குச் சமமாகவும், A−இல் இருந்து B−ன் திசையும் C−இல் இருந்து D−இன் திசையும் ஒரே திசையாகவும் இருந்தால், இருந்தால் மட்டுமே மற்றும் என்ற இரு வெக்டர்கள் சமவெக்டர்கள் எனப்படும். இதனை  = என எழுதுவோம். இங்கு என்பது –ன் நகர்வு எனப்படும்.

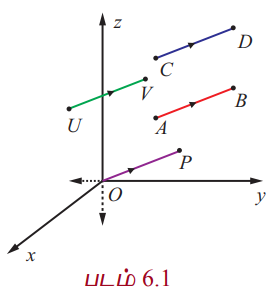
ℝ3 −ல் உள்ள எந்தவொரு வெக்டர் −யையும் ℝ3 -ல் எங்கு வேண்டுமானாலும் நகர்த்தி, ∪ ∈ ℝ3 என்ற புள்ளியை தொடக்கப்புள்ளியாகவும் V ∈ ℝ3 என்ற புள்ளியை முடிவுப் புள்ளியாகவும் கொண்ட ஒரு வெக்டருக்குச் சமமாக 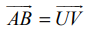  எனுமாறு எழுத முடியும் எனக் காண்கிறோம். குறிப்பாக, ℝ3 −ன் ஆதிப்புள்ளி O எனில், P ∈ ℝ3 என்ற புள்ளியை 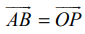எனுமாறு காணலாம்.

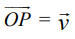என்ற வெக்டர் P என்ற புள்ளியின் நிலை வெக்டர் எனப்படும். மேலும், கொடுக்கப்பட்ட ஏதேனுமொரு வெக்டர் −க்கு, P ∈ ℝ3 என்ற தனித்த புள்ளியை எனுமாறு காணலாம். என்ற வெக்டரின் தொடக்கப்புள்ளி A−யும் முடிவுப்புள்ளி B−யும் ஒன்றாக அமைந்தால், அவ்வெக்டர் பூச்சிய வெக்டர் எனப்படும். (1,0,0), (0,1,0), (0,0,1), மற்றும் (0,0,0) என்ற புள்ளிகளின் நிலை வெக்டர்களை முறையே 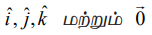ஆகிய வழக்கமான குறியீடுகளால் குறிப்பிடுகிறோம். கொடுக்கப்பட்ட ஒரு புள்ளி (a1, a2, a3) ∈ ℝ3 −ன் நிலைவெக்டர்  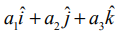 எனப்படும். இது (0,0,0) என்ற புள்ளியை தொடக்கப் புள்ளியாகவும், (a1, a2, a3) என்ற புள்ளியை முடிவுப் புள்ளியாகவும் கொண்ட கோட்டுத்துண்டாகும். அனைத்து மெய்யெண்களும் திசையிலிகள் எனப்படும்.

A என்பது (a1, a2, a3) மற்றும் B என்பது (b1, b2, b3) எனில் வெக்டரின் நீளம் 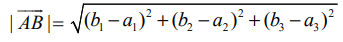  ஆகும். குறிப்பாக (b1,b2,b3)−ன் நிலைவெக்டர்   எனில், இதன் நீளம் 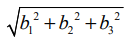  ஆகும். நீளம் 1 உடைய வெக்டரை அலகு வெக்டர் என்கிறோம். அலகு வெக்டரைக் குறிப்பிட்ட என்ற குறியீட்டைப் பயன்படுத்துகிறோம். 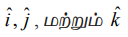  ஆகியவை அலகு வெக்டர்கள் என்பதையும், நீளம் 0 கொண்ட ஒரேயொரு வெக்டர்   என்பதையும் நினைவில்கொள்க.

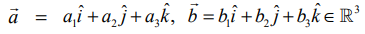மற்றும் α ∈ ℝ எனில், முப்பரிமாண வெளியில் வெக்டர்களின் கூட்டல் மற்றும் திசையிலிப் பெருக்கல் ஆகியவற்றை பின்வருமாறு வரையறுக்கிறோம்.

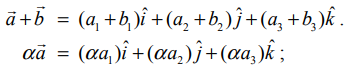
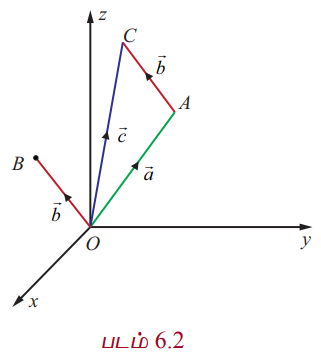
–ன் வடிவக்கணித விளக்கம் காண, A = (a1, a2, a3)  மற்றும் B = (b1, b2, b3) என்ற புள்ளிகளின் நிலைவெக்டர்கள் முறையே என்க. A என்ற புள்ளியை தொடக்கப் புள்ளியாகவும், பொருத்தமான ஒரு புள்ளி (c1, c2, c3) ∈ ℝ3 யை முடிவுப்புள்ளியாகவும் கொண்ட வெக்டருக்கு நிலைவெக்டர் யை நகர்த்தினால் படம் (6.2), (c1, c2, c3) புள்ளியின் நிலைவெக்டர் ஆனது யைக் குறிக்கும்.

எனும் வெக்டர் எனும் வெக்டருக்கு இணையாக உள்ள வெக்டராகும். a>1 எனில் –ன் நீளம் α மடங்கு பெரிதாக்கப்படுகிறது. 0<α<1 எனில் ன் நீளம் α மடங்கு குறுக்கப்படுகிறது. a<0 எனில்  ன் எண்ணளவு -ன் எண்ணளவைப் போல் |α| மடங்காகவும் ன் திசை -ன் திசைக்கு எதிர்த்திசையிலும் இருக்கும். குறிப்பாக α =−1 எனில் =− என்ற வெக்டரின் நீளமானது -ன் நீளத்திற்குச் சமமாகவும் −ன் திசைக்கு எதிர்திசையிலும் அமையும். படம். 6.3