எண்கள்

இயல் 1

எண்கள்

கற்றல் நோக்கங்கள்:

● பகா மற்றும் பகு எண்களை அடையாளம் காணுதல்.

● வகுபடும் தன்மை விதிகளை அறிதல், அதனைப் பயன்படுத்தி ஓர் எண்ணின் காரணிகளைக் காணுதல்.

● ஒரு பகு எண்ணை, பகா எண்களின் பெருக்கற்பலனாக எழுதுதல்.

● இரண்டு அல்லது அதற்கு மேற்பட்ட எண்களுக்கு மீப்பெரு பொதுக் காரணி (மீ.பெ.கா) மற்றும் மீச்சிறு பொது மடங்கைக் (மீ.சி.ம) காணுதல் மற்றும் அவற்றை அன்றாட வாழ்க்கைச் சூழலில் பயன்படுத்துதல்.

நினைவு கூர்தல்:

1. ஒற்றை மற்றும் இரட்டை எண்கள்

• ஓர் எண்ணை இரண்டு சம குழுக்களாகப் (இரண்டு இரண்டாக) பகுக்க இயலாது எனில், அது ஒற்றை எண் எனப்படும்.

1, 3, 5, 7,..., 73, 75,..., 2009, ... ஆகியவை 'ஒற்றை எண்கள்' ஆகும்.

• ஓர் எண்ணை இரண்டு சம குழுக்களாகப் (இரண்டு இரண்டாக) பகுக்க இயலும் எனில், அது இரட்டை எண் எனப்படும்.

2, 4, 6, 8,.., 68, 70,, 4592, ஆகியவை 'இரட்டை எண்கள்’ ஆகும்.

• எல்லா ஒற்றை எண்களும் 1, 3, 5, 7 அல்லது 9 ஆகிய ஏதாவது ஓர் இலக்கத்தில் முடியும். 

• எல்லா இரட்டை எண்களும் 0, 2, 4, 6 அல்லது 8 ஆகிய ஏதாவது ஓர் இலக்கத்தில் முடியும். 

• முழு எண்களில், ஒற்றை எண்களும் இரட்டை எண்களும் அடுத்தடுத்து வரும்.

இவற்றை முயல்க

(i) கவனித்து நிறைவு செய்க

1 + 3 = ?

5 + 11 = ?

21 + 47 = ?

____+_____ = ?

இதிலிருந்து நாம் முடிவு செய்வது யாதெனில் "இரு ஒற்றை எண்களின் கூடுதலானது எப்போதும் ஓர்__________ ஆகும்".

விடை:

1 + 3 = 4 

5 + 11 = 16

21 + 47 = 68 

ஒரு ஒற்றை எண் + மற்றொரு ஒற்றை எண் = ஒரு இரட்டை எண். இதிலிருந்து நாம் முடிவு செய்வது யாதெனில் "இரு ஒற்றை எண்களின் கூடுதலானது எப்போதும் ஒரு இரட்டை எண் ஆகும்.

(ii) கவனித்து நிறைவு செய்க

5 × 3 = ? 

7 ×  9 = ?

11 × 13 = ?

_____×_______= ?

இதிலிருந்து நாம் முடிவு செய்வது யாதெனில் “இரு ஒற்றை எண்களின் பெருக்கற்பலன் எப்போதும் ஓர்__________ஆகும்".

விடை:

5 × 3 = 15 

7 × 9 = 63

11 × 13 = 143 

ஒரு ஒற்றை எண் × மற்றொரு ஒற்றை எண் = ஒற்றை எண். 

இதிலிருந்து நாம் முடிவு செய்வது யாதெனில் இரு ஒற்றை எண்களின் பெருக்கற்பலன் எப்போதும் ஒரு ஒற்றை எண் ஆகும்.

பின்வரும் கூற்றுகளைத் தகுந்த எடுத்துக்காட்டுகளுடன் மெய்ப்பிக்க.

(iii) ஓர் ஒற்றை எண்ணையும் ஓர் இரட்டை எண்ணையும் கூட்டினால் எப்போதும் ஓர் ஒற்றை எண்ணே கிடைக்கும்.

விடை : 

ஓர் ஒற்றை எண் = 5

ஓர் இரட்டை எண் = 10 என்க. 

அவற்றின் கூட்டல் 5 + 10 = 15, ஓர் ஒற்றை எண். 

ஓர் ஒற்றை எண்ணையும் ஓர் இரட்டை எண்ணையும் கூட்டினால்  எப்போதும் ஓர் ஒற்றை எண்ணே கிடைக்கும்.

 (iv) ஓர் ஒற்றை எண்ணையும் ஓர் இரட்டை எண்ணையும் பெருக்கினால் எப்போதும் ஓர் இரட்டை எண்ணே கிடைக்கும்.

விடை : 

ஓர் ஒற்றை எண் = 5

ஓர் இரட்டை எண் = 10 என்க. 

அவற்றின் பெருக்கல் பலன் = 5 × 10 = 50, ஓர் இரட்டை எண். 

ஓர் ஒற்றை எண்ணையும் ஓர் இரட்டை எண்ணையும் பெருக்கினால்   எப்போதும் ஓர் இரட்டை எண்ணே கிடைக்கும்.

 (v) மூன்று ஒற்றை எண்களைப் பெருக்கினால் எப்போதும் ஓர் ஒற்றை எண்ணே கிடைக்கும்.

விடை :

மூன்று ஒற்றை எண்கள் 7, 5, 3 என்க. 

இரு ஒற்றை எண்களின் பெருக்கல் பலன் ஓர் ஒற்றை எண். 

அதாவது 7 × 5 = 35, ஒற்றை எண். 

மேலும் 35 × 3 = 105, ஒற்றை எண்

7 × 5 × 3 = 105. 

மூன்று ஒற்றை எண்களின் பெருக்கல் பலன் எப்போதும் ஓர் ஒற்றை எண் ஆகும்.

குறிப்பு

• 1 என்ற எண் ஓர் ஒற்றை எண் ஆதலால் அதன் தொடரியான 2 ஓர் இரட்டை எண் ஆகும். ஆகவே, 1 இன் முன்னியான 0 என்ற எண்ணானது ஓர் இரட்டை எண் ஆகும்.

• இயல் எண்களில் முதல் எண் 1 ஆனது ஓர் ஒற்றை எண் மற்றும் முழு எண்களில் முதல் எண் 0 ஆனது ஓர் இரட்டை எண் ஆகும்.

2. காரணிகள்

இந்தச் சூழல் குறித்துச் சிந்திக்க:

ஆசிரியர் வேலவனிடம் 8 மற்றும் 20 என்ற இரு எண்களை வழங்கி அவற்றை இரு எண்களின் பெருக்கற்பலனாக எழுதச் சொல்கிறார். வேலவன் தனது கணித மனத்திறன் மற்றும் பெருக்கல் வாய்ப்பாடுகளைக் கொண்டு 8 = 2 × 4; 20 = 2 × 10 மற்றும் 20 = 4 × 5 என உடனடியாகக் காண்கிறான். இதிலிருந்து, நாம் 2 மற்றும் 4 ஆகிய எண்களை 8 இன் காரணிகள் எனக் கூறலாம். அவ்வாறே, 2, 4, 5 மற்றும் 10 ஆகிய எண்கள் 20 இன் காரணிகள் ஆகும்.

நாம் மேலும் 8 ஐ 1 × 8 என எழுதலாம். அதன் மூலம் 1 மற்றும் 8 ஆகிய எண்களும் 8 இன் காரணிகள் என முடிவு செய்கிறோம்.

இதிலிருந்து, நாம் கவனிப்பது,

• கொடுக்கப்பட்ட ஓர் எண்ணை மீதியின்றி வகுக்கும் ஓர் எண்ணானது அதன் 'காரணி' ஆகும்.

• ஒவ்வோர் எண்ணிற்கும், 1 மற்றும் அதே எண் காரணிகளாக அமையும்.

• ஓர் எண்ணின் ஒவ்வொரு காரணியும், அந்த எண்ணின் மதிப்பிற்குக் குறைவாகவோ அல்லது சமமாகவோ இருக்கும்.

3. மடங்குகள்

7 இன் பெருக்கல் அட்டவணையைப் பார்ப்போம்.

1 × 7 = 7

2 × 7 = 14

3 × 7 = 21

4 × 7 = 28

5 × 7 = 35...

இங்கு 7, 14, 21, 28, 35, … …  ஆகிய எண்கள் 7 இன் 'மடங்குகள்' ஆகும்.

இதிலிருந்து, நாம் உற்றுநோக்குவது,

• ஓர் எண்ணின் ஒவ்வொரு மடங்கும் அந்த எண்ணை விட அதிகமாகவோ அல்லது சமமாகவோ இருக்கிறது.

7 இன் மடங்குகளான 7, 14, 21, 28, ... ஆகியவை 7–ஐ விட அதிகமாகவோ அல்லது சமமாகவோ இருக்கின்றன.

• ஓர் எண்ணின் மடங்குகள் முடிவற்றவை.

5 இன் மடங்குகளான 5, 10, 15, 20, ... ஆகியவை முடிவற்றவை.

 இவற்றை முயல்க

 (i) சரியா, தவறா எனக் கூறுக

அ) மிகச் சிறிய ஒற்றை இயல் எண் 1 ஆகும். [சரி]

ஆ) 2 என்ற எண்ணானது மிகச் சிறிய இரட்டை முழு எண் ஆகும். [தவறு]

இ) 12345 + 5063 என்பது ஓர் ஒற்றை எண் ஆகும். [தவறு]

ஈ) ஒவ்வோர் எண்ணிற்கும் அதே எண் ஒரு காரணியாக அமையும். [சரி]

உ) 6 இன் மடங்கான ஓர் எண்ணானது, 2 மற்றும் 3 இன் மடங்காகவும் இருக்கும். [சரி]

(ii) 7 என்பது 27 இன் ஒரு காரணியா?

தீர்வு :

7 என்பது 27 இன் ஒரு காரணி அல்ல

ஏனெனில் 7 ஆனது 27 ஐ மீதியின்றி வகுப்பதில்லை

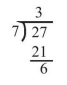
(iii) 12 என்ற எண், 12 என்ற எண்ணுக்குக் காரணியாகுமா? அல்லது மடங்காகுமா?

தீர்வு :

12 இன் காரணிகள் 1, 2, 3, 4, 6, 12

12 இன் மடங்குகள் 12, 24, 36, 48, ........ 

எனவே 12 என்ற எண், 12 என்ற எண்ணின் காரணி மற்றும் மடங்கு ஆகும்.

(iv) 30 என்ற எண், 10 இன் மடங்கா? காரணியா?

விடை: 

ஒரு எண்ணின் காரணி அந்த எண்ணை விட குறைவாகவோ அல்லது சமமாகவோ இருக்கும்

30 < 10 .

∴ 30 என்ற எண் 10 இன் மடங்கு ஆகும். 

(v) பின்வரும் எண்களில் எது 3–ஐக் காரணியாகக் கொண்டுள்ளது? 

அ) 8 

ஆ) 10 

இ) 12 

ஈ)  14

விடை :  (இ) 12

(∴ 12 இன் காரணிகள் 1, 2, 3, 4, 6, 12) 

(vi) 24 இன் காரணிகள் 1, 2, 3, 6, 12 மற்றும் 24. இதில் விடுபட்ட காரணிகளைக் கண்டறிக.

விடை: 

24 இன் காரணிகள் 1, 2, 3, 4, 6, 8, 12, 24

விடுபட்ட காரணிகள் 4 மற்றும் 8. 

(vii) பின்வரும் எண்களை உற்று நோக்கி, விடுபட்டவற்றைக் கண்டறிக:

விடை :

9 இன் மடங்கு 9, 18, 27, 36, 45, 54

4 இன் மடங்கு 4, 8, 12, 16, 20, 24

அறிமுகம்

முதல் பருவத்தில் நாம் இயல் மற்றும் முழு எண்களைப் பற்றிக் கற்றோம். தற்பொழுது, நாம் சிறப்பு எண்களான பகா மற்றும் பகு எண்கள், எண்களின் வகுபடும் தன்மை விதிகள், மீப்பெரு பொதுக் காரணி (மீ.பெ.கா) மற்றும் மீச்சிறு பொது மடங்கு (மீ.சி.ம) பற்றி அறிவோம்.

எங்கும் கணிதம் – அன்றாட வாழ்வில் எண்கள்

ஒரு நிறுவனத்தின் தகவல்களைப் பாதுகாக்கும் சாவியாகப் பகா எண்களைப் பயன்படுத்துதல் (பெரிய பகு எண்களை இரு பெரிய பகா எண்களின் பெருக்கற்பலனாக அமைத்தல்)

அன்றாட வாழ்வில் மீப்பெரு பொதுக் காரணி