வட்டத்தின் பகுதிகள்: எடுத்துக்காட்டு கணக்குகள்

எடுத்துக்காட்டு 2.1 

ஒரு வட்டக்கோணப் பகுதியின் ஆரம் 21 செ.மீ மற்றும் அதன் மையக்கோணம் 120° எனில், அதன் 

(i) வில்லின் நீளம் 

(ii) பரப்பளவு 

(iii) சுற்றளவு காண்க. (π = 22/7)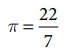

தீர்வு :

எடுத்துக்காட்டு 2.2

35 செ.மீ. ஆரமுள்ள வட்ட வடிவிலான ஜிம்னாஸ்டிக் வளையமானது 5 சம அளவுள்ள விற்களாகப் பிரிக்கப்பட்டு வெவ்வேறு நிறங்களில் வண்ணமிடப்பட்டுள்ளது எனில், ஒவ்வொரு வட்ட வில்லின் நீளத்தையும் காண்க 

தீர்வு :

ஆரம், r = 35 செ.மீ மற்றும் n = 5. 

வட்ட வில்லின் நீளம், l = (1 / n) × 2πr அலகுகள்

= (1/5) × 2 × π × 35 = 14π செ.மீ

எடுத்துக்காட்டு 2.3

7.5 செ.மீ. ஆரமுள்ள ஒரு ஸ்பின்னரானது ஆறு சம அளவுள்ள வட்டக்கோணப் பகுதிகளாகப் பிரிக்கப்பட்டுள்ளது எனில், ஒவ்வொரு வட்டக்கோணப் பகுதியின் பரப்பளவையும் காண்க. 

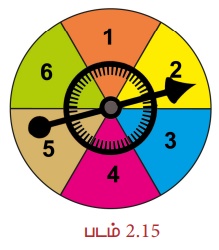
தீர்வு:

ஆரம், r = 7.5 செ.மீ மற்றும் n = 6. 

வட்டக்கோணப் பகுதியின் பரப்பளவு, A = (1/ n) × πr2 

= (1/6) × π × 7.5 × 7.5 

= 9.375π செ.மீ2

எடுத்துக்காட்டு 2.4

கமலேஷ் என்பவர் 70 செ.மீ. ஆரமுள்ள வட்ட வடிவ உணவுமேசையும், தருண் என்பவர் 140 செ.மீ. ஆரமுள்ள கால்வட்ட வடிவ உணவுமேசையும் வைத்துள்ளனர் எனில், யாருடைய உணவுமேசை அதிகப் பரப்பளவைக் கொண்டுள்ளது? (π = 22 / 7)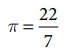

தீர்வு: 

கமலேஷ் என்பவரின் வட்டவடிவ உணவுமேசையின் பரப்பளவு = πr2 ச.அ

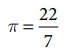× 70 × 70 

A = 15400 செ.மீ2 (தோராயமாக).

தருண் என்பவரின் கால்வட்டவடிவ உணவுமேசையின் பரப்பளவு = 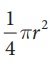ச.அ

= (1 / 4) × (22 / 7) × 140 × 140

A = 15400 செ.மீ2 (தோராயமாக).

ஆகவே, இருவரின் உணவுமேசைகளும் சம அளவு பரப்பளவைக் கொண்டுள்ளன.

சிந்திக்க 

ஒரு வட்டத்தின் ஆரம் இருமடங்கு அதிகரித்தால், கிடைக்கும் புதிய வட்டத்தின் பரப்பளவு என்னவாக இருக்கும்?

எடுத்துக்காட்டு 2.5

7 செ.மீ விட்டமுள்ள நான்கு பதக்கங்களைப் படம் 2.18 இல் உள்ளவாறு வைக்கும் பொழுது, இடையில் அடைபடும் நிழலிடப்பட்ட பகுதியின் பரப்பளவைக் காண்க (π = 22/7)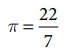

தீர்வு: 

நிழலிடப்பட்ட பகுதியின் பரப்பளவு = சதுரத்தின் பரப்பளவு – (4 × கால்வட்டங்களின் பரப்பளவு )

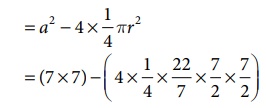
= 49 − 38.5 

= 10.5 செ.மீ2 (தோராயமாக)