அளவைகள் | அலகு 2 | 8 ஆம் வகுப்பு கணக்கு - வட்டத்தின் பகுதிகள் | 8th Maths : Chapter 2 : Measurements
8 ஆம் வகுப்பு கணக்கு : அலகு 2 : அளவைகள்
வட்டத்தின் பகுதிகள்
வட்டத்தின் பகுதிகள்

வட்டம் என்பது ஒரு தளத்திலுள்ள ஒரு நிலையான புள்ளியிலிருந்து சம தொலைவில் நகரும் புள்ளியின் நியமப்பாதை ஆகும். நிலையான புள்ளியானது வட்ட மையம் என்றும், சமதொலைவு ஆனது ஆரம் என்றும் அழைக்கப்படுகின்றன.
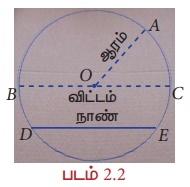
மேலும், வட்டத்தின் மீதுள்ள ஏதேனும் இரு புள்ளிகளை இணைக்கும் கோட்டுத்துண்டு நாண் எனப்படும். ஒரு நாண், வட்டத்தை இரு பகுதிகளாகப் பிரிக்கிறது. வட்டத்தின் மையப்புள்ளி வழியே செல்லும் நான் விட்டம் ஆகும். ஒரு வட்டத்தின் விட்டமானது, அந்த வட்டத்தை இரு சம அளவுள்ள வட்டத்துண்டுகளாகப் பிரிக்கிறது. மேலும், அது வட்டத்தின் மிகப்பெரிய நாண் ஆகும்.
செயல்பாடு
1.. ஒரு காகிதத்தில், வளையலைப் பயன்படுத்தி ஒரு வட்டம் வரைந்து அதைத் தனியாக வெட்டி எடுத்துக்கொள்க. வட்டத்தின் பரிதியில் ஏதேனும் இரு புள்ளிகளை A மற்றும் B எனக் குறிக்க. A மற்றும் B வழியே வட்டத்தை மடிக்க. இப்பொழுது கிடைக்கும் மடிப்புக் கோடு நாணைக் குறிக்கிறது.
2. காகிதமடிப்பு முறையில், ஒரு வட்டத்தின் இரண்டு விட்டங்கள் மற்றும் அதன் மையம் ஆகியவற்றைக் கண்டுபிடி.
3. ஒரு வட்டத்தின் விட்டமானது ஆரத்தைப் போல் இருமடங்கு ஆகும் என்பதைச் சரிபார்க்க.
1. வட்டவில் மற்றும் வட்டக்கோணப் பகுதி
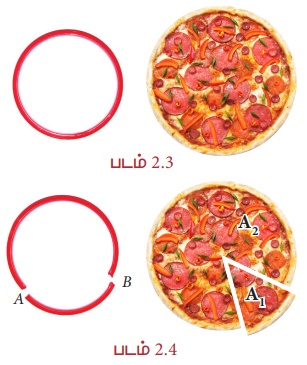
படம் 2.3 இல் கொடுக்கப்பட்டுள்ள கண்ணாடி வளையலையும், வேகப்பத்தையும் (Pizza) உற்று நோக்குக. இரண்டும் வட்ட வடிவில் இருந்தாலும், வளையலானது வட்டத்தைச் சுற்றி அமைந்திருக்கும் எல்லையையும், வேகப்பமானது எல்லைக்குள் அடைபடும் சமதளப் பகுதியையும் குறிக்கிறது. அதாவது வளையல் வட்டத்தின் பரிதியையும், வேகப்பம் வட்டத்தின் பரப்பளவையும் குறிப்பதாக அமைகின்றது.
அவற்றிலிருந்து ஒரு பகுதியைப் படம் 2.4 இல் காட்டியுள்ளவாறு வெட்டியெடுப்பதாகக் கொள்வோம். வளையல் துண்டுகள் ஒவ்வொன்றும் வட்டவில்லைக் குறிக்கிறது. ![]() என்பது சிறிய வட்டவில்லையும்,
என்பது சிறிய வட்டவில்லையும், ![]() பெரிய வட்டவில்லையும் குறிக்கிறது. அதேபோன்று வேகப்பத்தின் பகுதிகள்
பெரிய வட்டவில்லையும் குறிக்கிறது. அதேபோன்று வேகப்பத்தின் பகுதிகள்
ஒவ்வொன்றும் வட்டக்கோணப்பகுதியைக் குறிக்கிறது. A1 என்பது சிறிய வட்டக்கோணப்பகுதியையும், A2 என்பது பெரிய வட்டக்கோணப் பகுதியையும் குறிக்கிறது.
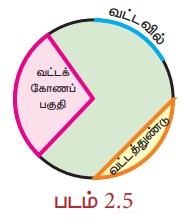
* ஒரு வட்டத்தின் வட்டப் பரிதியின் ஒரு பகுதியே வட்டவில் ஆகும்.
* ஒரு வட்டத்தின் இரண்டு ஆரங்களாலும், அந்த ஆரங்களால் வட்டப் பரிதியில் வெட்டப்படும் வில்லாலும் அடைபடும் சமதளப்பகுதி வட்டக்கோணப்பகுதி ஆகும்
* ஒரு நாண் வட்டத்தை இரு பகுதிகளாகப் பிரிக்கிறது. ஒவ்வொரு பகுதியும் வட்டத்துண்டு என அழைக்கப்படுகிறது.
குறிப்பு
பெரிய வட்டவில்லினைத் தாங்கும் வட்டப்பகுதி 'பெரிய வட்டத்துண்டு' என்றும் சிறிய வட்டவில்லினைத் தாங்கும் வட்டப்பகுதி 'சிறிய வட்டத்துண்டு’ என்றும் அழைக்கப்படுகிறது.

சிந்திக்க
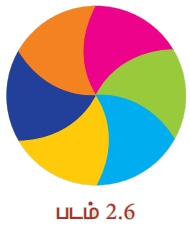
படத்தில் உள்ள வட்டம் ஆறு சம பாகங்களாகப் பிரிக்கப்பட்டுள்ளது அவற்றை வட்டக்கோணப் பகுதிகள் என்று கூறலாமா? ஏன்?
வட்டமையக்கோணம்
ஒரு வட்டக்கோணப் பகுதியானது, அவ்வட்டத்தின் மையத்தில் ஏற்படுத்தும் கோணம் வட்டமையக்கோணம் ஆகும். வட்டமையக்கோணத்தின் உச்சியானது வட்டத்தின் மையம் ஆகும். அதன் இரு கைகளாக ஆரங்கள் உள்ளன. படம் 2.7 இல், நிழலிடப்பட்ட வட்டக்கோணப் பகுதியின் வட்டமையக்கோணம் ∠AOB = θ° (Theta என்று படிக்க வேண்டும்) மற்றும் அதன் இரு கைகள் OA மற்றும் OB ஆகியவை ஆரங்கள் ஆகும்.
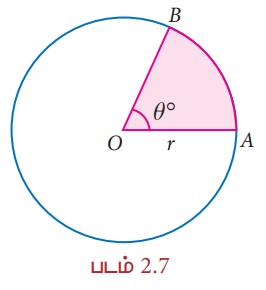
ஒரு வட்டத்தின் மையக்கோணம் 360° ஆகும். வட்டமானது 'n' சம அளவுள்ள வட்டக்கோணப் பகுதிகளாகப் பிரிக்கப்பட்டால் கிடைக்கும்,
வட்டக்கோணப் பகுதியின் மையக்கோணம்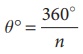 ஆகும்.
ஆகும்.
எடுத்துக்காட்டாக, அரைவட்டத்தின் மையக்கோணம் = 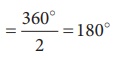 ஆகும்.
ஆகும்.
மற்றும் கால்வட்டத்தின் மையக்கோணம் = 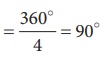 ஆகும்.
ஆகும்.
இவற்றை முயல்க
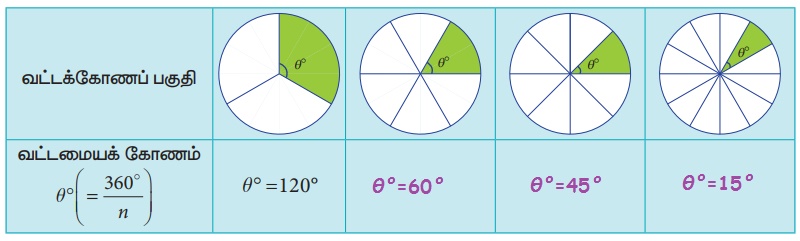
நிழலிடப்பட்ட வட்டக்கோணப்பகுதிகளின் மையக்கோணங்களைக் காண்க. (ஒவ்வொரு வட்டமும் சம அளவுள்ள வட்டக்கோணப்பகுதிகளாகப் பிரிக்கப்பட்டுள்ளது)
2. வட்டவில்லின் நீளம் மற்றும் வட்டக்கோணப்பகுதியின் பரப்பளவு
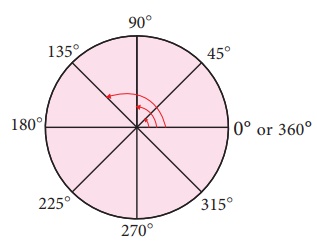
'r' அலகு ஆரமுள்ள ஒரு வட்டத்தின் மையத்தைச் சுற்றியுள்ள கோணம் 360° ஆகும்.
மேலும், வட்டத்தின் சுற்றளவு = 2πr அலகுகள் என்றும், அதன் பரப்பளவு = πr2 சதுர அலகுகள் என்றும் நாம் முன்னரே அறிந்திருக்கிறோம்.
முதலில் ஒரு வட்டத்தை எடுத்துக்கொள்வோம். ஒரு வட்டத்தை இரண்டு சம அளவுள்ள வட்டக்கோணப் பகுதிகளாகப் பிரித்தால், இரண்டு அரை வட்டங்களைப் பெறுகிறோம். அரைவட்டத்தின் வில்லின் நீளமானது, அவ்வட்டத்தின் சுற்றளவின் நீளத்தில் பாதியாகும் மற்றும் அரைவட்டத்தின் பரப்பளவானது, அந்த வட்டத்தின் பரப்பளவில் பாதியாகும்.
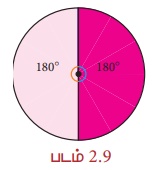
அரைவட்டத்தின் வில்லின் நீளம் = 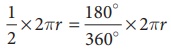 அலகுகள் ஆகும்.
அலகுகள் ஆகும்.
அரைவட்டத்தின் பரப்பளவு = 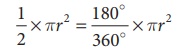 சதுர அலகுகள் ஆகும்.
சதுர அலகுகள் ஆகும்.
மேலும், ஒரு வட்டத்தை மூன்று சம அளவுள்ள வட்டக்கோணப்பகுதிகளாகப் பிரித்தால்,
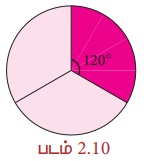
வட்டக்கோணப் பகுதியின் வில்லின் நீளம் = 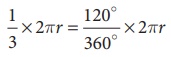 அலகுகள் ஆகும்.
அலகுகள் ஆகும்.
வட்டக்கோணப் பகுதியின் பரப்பளவு = 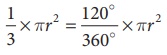 சதுர அலகுகள் ஆகும்.
சதுர அலகுகள் ஆகும்.
இதேபோன்று, ஒரு வட்டத்தை நான்கு சம அளவுள்ள வட்டக்கோணப் பகுதிகளாகப் பிரித்தால்,
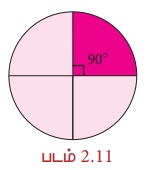
கால்வட்டத்தின் வில்லின் நீளம் = 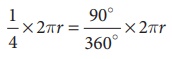 அலகுகள் ஆகும்.
அலகுகள் ஆகும்.
மற்றும் கால்வட்டத்தின் பரப்பளவு =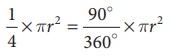 சதுர அலகுகள் ஆகும்.
சதுர அலகுகள் ஆகும்.
இதிலிருந்து நாம் அறிந்துகொள்வது என்ன?
ஒரு வட்டக்கோணப் பகுதியின் மையக்கோணத்திற்கும் அந்த வட்டத்தின் மையக்கோணத்திற்கும் இடையேயுள்ள விகிதத்தால் வட்டத்தின் சுற்றளவையும் பரப்பளவையும் பெருக்கினால், முறையே அந்த வட்டக்கோணப் பகுதியின் வில்லின் நீளத்தையும் பரப்பளவையும் நாம் கண்டறியலாம்.
அதாவது 'r' அலகு ஆரமுள்ள ஒரு வட்டக்கோணப்பகுதியின் மையக்கோணம் θ° எனக் கொள்வோம். மையக்கோணம் θ° இக்கும் 360° இக்கும் இடையேயுள்ள விகிதம் 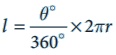 ஆகும்.
ஆகும்.
வட்டக்கோணப் பகுதியின் வில்லின் நீளம், l = 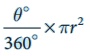 அலகுகள்
அலகுகள்
வட்டக்கோணப் பகுதியின் பரப்பளவு, A = 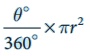 சதுர அலகுகள்
சதுர அலகுகள்
சிந்திக்க
மேலே, 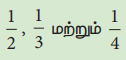 ஆகியவற்றுக்குப் பதிலாக முறையே நாம்
ஆகியவற்றுக்குப் பதிலாக முறையே நாம் 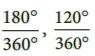 மற்றும்
மற்றும் ![]() ஆல் பெருக்குகிறோம். ஏன்?
ஆல் பெருக்குகிறோம். ஏன்?
குறிப்பு
1. 'r' அலகு ஆரமுள்ள ஒரு வட்டமானது n சமபாகங்களாகப் பிரிக்கப்பட்டால் கிடைக்கும்,
வட்டக்கோணப் பகுதியின் வில்லின் நீளம், 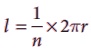 அலகுகள் மற்றும்
அலகுகள் மற்றும்
வட்டக்கோணப் பகுதியின் பரப்பளவு, 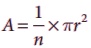 ச.அலகுகள்.
ச.அலகுகள்.
2. மேலும், வட்டக்கோணப் பகுதியின் பரப்பளவு,
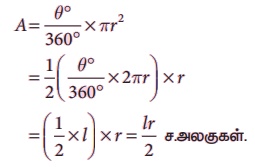
3. வட்டக்கோணப் பகுதியின் சுற்றளவு
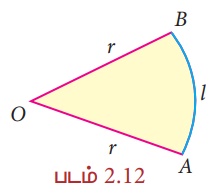
ஒரு மூடிய பகுதியின் எல்லையின் மொத்த நீளமே அதன் சுற்றளவாகும் என்பதை நாம் ஏற்கனவே அறிவோம் அல்லவா? வட்டக்கோணப்பகுதியின் எல்லையாக எவை அமைந்துள்ளன? இரண்டு ஆரங்கள் (OA மற்றும் OB) மற்றும் ஒரு வட்டவில் ![]() .
.
எனவே, வட்டக்கோணப் பகுதியின் சுற்றளவு, P = வட்டவில்லின் நீளம் + இரு ஆரங்களின் நீளம்.
P = l + 2r அலகுகள்.
∴ வட்டக்கோணப் பகுதியின் சுற்றளவு, P = l + 2r அலகுகள் ஆகும்.
உங்களுக்குத் தெரியுமா?
கணித வரலாற்றில் தமிழருக்கு என்றென்றும் முதன்மையான இடம் உண்டு. வட்டத்திற்கான பரப்பளவைக் காணும் முறையைச் சில ஆயிரம் ஆண்டுகளுக்கு முன்பே, கணக்கதிகாரம் என்னும் நூலில் தமிழர்கள் பாடல் வடிவில் பதிவு செய்துள்ளனர்.
"வட்டத்தரை கொண்டு விட்டத்தரை தாக்கச் சட்டெனத் தோன்றும் குழி"
பொருள்:
வட்டத்தரை என்பது சுற்றளவில் பாதியையும், விட்டத்தரை என்பது விட்டத்தில் பாதி ஆரத்தையும் மற்றும் குழி என்பது பரப்பளவையும் குறிக்கும். அதாவது சுற்றளவில் பாதியை, விட்டத்தில் பாதியான ஆரத்தால் பெருக்கினால் வட்டத்தின் பரப்பளவு கிடைக்கும்.
வட்டத்தின் பரப்பளவு = வட்டத்தரை × விட்டத்தரை
= (1 / 2) × வட்டத்தின் சுற்றளவு × (1 / 2) × வட்டத்தின் விட்டம்
= [ (1/2) × (2πr) ] × r
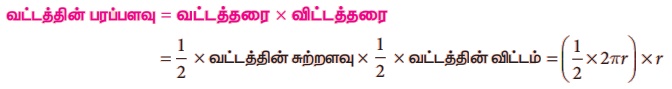
ஃ வட்டத்தின் பரப்பளவு, A = πr2 சதுர அலகுகள்.
குறிப்பு
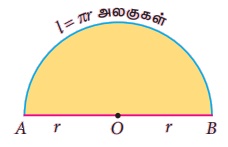
1. அரைவட்டத்தின் சுற்றளவு,
P = l + 2r அலகுகள்
= πr + 2r
= (π + 2) r அலகுகள்.
2. கால் வட்டத்தின் சுற்றளவு,
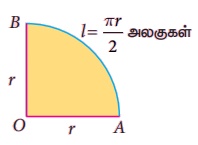
P = l + 2r
= (πr / 2) + 2r
= [(π / 2) + 2] r அலகுகள்
எடுத்துக்காட்டு 2.1
ஒரு வட்டக்கோணப் பகுதியின் ஆரம் 21 செ.மீ மற்றும் அதன் மையக்கோணம் 120° எனில், அதன்
(i) வில்லின் நீளம்
(ii) பரப்பளவு
(iii) சுற்றளவு காண்க. (π = 22/7) 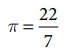
தீர்வு :

எடுத்துக்காட்டு 2.2
35 செ.மீ. ஆரமுள்ள வட்ட வடிவிலான ஜிம்னாஸ்டிக் வளையமானது 5 சம அளவுள்ள விற்களாகப் பிரிக்கப்பட்டு வெவ்வேறு நிறங்களில் வண்ணமிடப்பட்டுள்ளது எனில், ஒவ்வொரு வட்ட வில்லின் நீளத்தையும் காண்க

தீர்வு :
ஆரம், r = 35 செ.மீ மற்றும் n = 5.
வட்ட வில்லின் நீளம், l = (1 / n) × 2πr அலகுகள்
= (1/5) × 2 × π × 35 = 14π செ.மீ
எடுத்துக்காட்டு 2.3
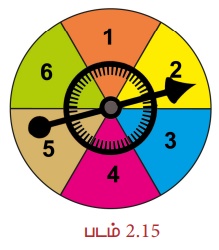
7.5 செ.மீ. ஆரமுள்ள ஒரு ஸ்பின்னரானது ஆறு சம அளவுள்ள வட்டக்கோணப் பகுதிகளாகப் பிரிக்கப்பட்டுள்ளது எனில், ஒவ்வொரு வட்டக்கோணப் பகுதியின் பரப்பளவையும் காண்க.
தீர்வு:
ஆரம், r = 7.5 செ.மீ மற்றும் n = 6.
வட்டக்கோணப் பகுதியின் பரப்பளவு, A = (1/ n) × πr2
= (1/6) × π × 7.5 × 7.5
= 9.375π செ.மீ2
எடுத்துக்காட்டு 2.4
கமலேஷ் என்பவர் 70 செ.மீ. ஆரமுள்ள வட்ட வடிவ உணவுமேசையும், தருண் என்பவர் 140 செ.மீ. ஆரமுள்ள கால்வட்ட வடிவ உணவுமேசையும் வைத்துள்ளனர் எனில், யாருடைய உணவுமேசை அதிகப் பரப்பளவைக் கொண்டுள்ளது? (π = 22 / 7) 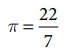
தீர்வு:
கமலேஷ் என்பவரின் வட்டவடிவ உணவுமேசையின் பரப்பளவு = πr2 ச.அ

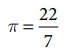 × 70 × 70
× 70 × 70
A = 15400 செ.மீ2 (தோராயமாக).
தருண் என்பவரின் கால்வட்டவடிவ உணவுமேசையின் பரப்பளவு = 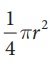 ச.அ
ச.அ

= (1 / 4) × (22 / 7) × 140 × 140
A = 15400 செ.மீ2 (தோராயமாக).
ஆகவே, இருவரின் உணவுமேசைகளும் சம அளவு பரப்பளவைக் கொண்டுள்ளன.
சிந்திக்க
ஒரு வட்டத்தின் ஆரம் இருமடங்கு அதிகரித்தால், கிடைக்கும் புதிய வட்டத்தின் பரப்பளவு என்னவாக இருக்கும்?
எடுத்துக்காட்டு 2.5
7 செ.மீ விட்டமுள்ள நான்கு பதக்கங்களைப் படம் 2.18 இல் உள்ளவாறு வைக்கும் பொழுது, இடையில் அடைபடும் நிழலிடப்பட்ட பகுதியின் பரப்பளவைக் காண்க (π = 22/7) 

தீர்வு:
நிழலிடப்பட்ட பகுதியின் பரப்பளவு = சதுரத்தின் பரப்பளவு – (4 × கால்வட்டங்களின் பரப்பளவு )
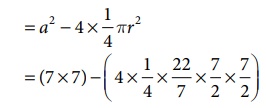
= 49 − 38.5
= 10.5 செ.மீ2 (தோராயமாக)