ஒட்டுறவுப் போக்குப் பகுப்பாய்வு

ஒட்டுறவுப் போக்குப் பகுப்பாய்வு (Regression Analysis)

அடுத்தாக நாம் கற்கவிருப்பது ஒட்டுறவுப் பகுப்பாய்வு ஆகும். 'ரெக்கரசன்' (Regression) என்ற வார்த்தையினை முதன்முதலில் (1877ல்)  உருவாக்கியவர் ஃபிரான்ஸிஸ் கால்டன் ஆவார். தனது ஆய்விற்காக தந்தைகளின் உயரத்திற்கும் மகன்களின் உயரத்திற்கும் உள்ள தொடர்பினை அறிய முற்படும்பொழுது குறிப்பிட்ட உயரமுடைய பெற்றோர்களுக்குப் பிறந்த குழந்தைகளின் சராசரி உயரம் மொத்த தொகுதிக்குமான சராசரி மதிப்பை நோக்கிச் செல்கின்றது என்பதை உறுதிபடுத்தினார். இப்பெயர் காரணத்தைக் கொண்டு அவர் இதற்கு 'ரெக்கரசன்' (Regression) என பெயரிட்டார். இதன் பொருள் சராசரியை நோக்கித் திரும்பிச் செல்லுதல் (Act of go back) அல்லது திரும்பிப் பார்த்தல் (Act of see back) என்பதாகும். மேற்சொன்ன நிகழ்வினை "கால்டனின் பின்னோக்கிச் செல்லும் பொது விதி" (Galton's Law of universal Regression) 1000 குடும்பத்திலுள்ளவர்களின் உயரத்தை சேகரித்து உறுதிப்படுத்தினர் ஒட்டுறவு என்ற சொல்லின் விளக்கம் - சராசரியை நோக்கிப் பின் செல்லுதல் - ஆகும்.

ஒட்டுறவு என்பது இரு மாறிகளுக்கிடையே உள்ள உறவை விளக்குகின்றது. Y சார்பு மாறி என்றும் X தனித்த மாறி என்றும் எடுத்துக்கொண்டால் இரு மாறிகளுக்கு இடையே உள்ள நேர்கோட்டுத் தொடர்பு X இன் மீது Y சார்ந்த ஒட்டுறவுக் கோட்டுச் சமன்பாடு எனப்படுகின்றது. இதைப்பயன்படுத்தி ஒரு குறிப்பிட்ட, தெரிந்த X மதிப்புக்கு y மதிப்பு என்ன என்பதைக் கணிக்கலாம். இந்தக் கோடே ஒட்டுறவு மாற்றத்தை அல்லது பின்னோக்கிச் செல்லல் என்ற கருத்தை விளக்கும் கால்டலான் ஒட்டுறவுக்கோடு என அழைக்கப்பட்டதாகும்.

உடன் தொடர்பிற்கும் ஒட்டுறவிற்கும் இடையே உள்ள வேறுபாடுகள்

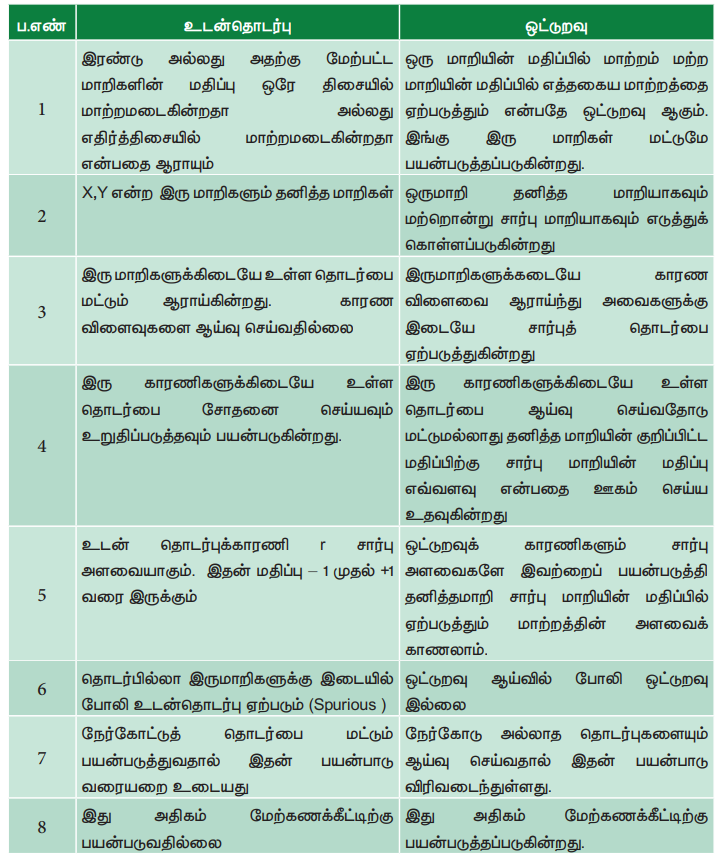
உடன் தொடர்பு

1. இரண்டு அல்லது அதற்கு மேற்பட்ட மாறிகளின் மதிப்பு ஒரே திசையில் மாற்றமடைகின்றதா அல்லது எதிர்த்திசையில் மாற்றமடைகின்றதா என்பதை ஆராயும்

2. X,Y என்ற இரு மாறிகளும் தனித்த மாறிகள்

3. இரு மாறிகளுக்கிடையே உள்ள தொடர்பை மட்டும் ஆராய்கின்றது. காரண விளைவுகளை ஆய்வு செய்வதில்லை

4. இரு காரணிகளுக்கிடையே உள்ள தொடர்பை சோதனை செய்யவும் உறுதிப்படுத்தவும் பயன்படுகின்றது.

5. உடன் தொடர்புக்காரணி r சார்பு அளவையாகும். இதன் மதிப்பு - 1 முதல் +1 வரை இருக்கும்

6. தொடர்பில்லா இருமாறிகளுக்கு இடையில் போலி உடன்தொடர்பு ஏற்படும் (Spurious )

7. நேர்கோட்டுத் தொடர்பை மட்டும் பயன்படுத்துவதால் இதன் பயன்பாடு வரையறை உடையது

8. இது அதிகம் மேற்கணக்கீட்டிற்கு பயன்படுவதில்லை

ஒட்டுறவு

1. ஒரு மாறியின் மதிப்பில் மாற்றம் மற்ற மாறியின் மதிப்பில் எத்தகைய மாற்றத்தை ஏற்படுத்தும் என்பதே ஒட்டுறவு ஆகும். இங்கு இரு மாறிகள் மட்டுமே பயன்படுத்தப்படுகின்றது.

2. ஒருமாறி தனித்த மாறியாகவும் மற்றொன்று சார்பு மாறியாகவும் எடுத்துக் கொள்ளப்படுகின்றது

3. இருமாறிகளுக்கடையே காரண விளைவை ஆராய்ந்து அவைகளுக்கு இடையே சார்புத் தொடர்பை ஏற்படுத்துகின்றது

4. இரு காரணிகளுக்கிடையே உள்ள தொடர்பை ஆய்வு செய்வதோடு மட்டுமல்லாது தனித்த மாறியின் குறிப்பிட்ட மதிப்பிற்கு சார்பு மாறியின் மதிப்பு எவ்வளவு என்பதை ஊகம் செய்ய உதவுகின்றது

5. ஒட்டுறவுக் காரணிகளும் சார்பு அளவைகளே இவற்றைப் பயன்படுத்தி தனித்தமாறி சார்பு மாறியின் மதிப்பில் ஏற்படுத்தும் மாற்றத்தின் அளவைக் காணலாம்.

6. ஒட்டுறவு ஆய்வில் போலி ஒட்டுறவு இல்லை

7. நேர்கோடு அல்லாத தொடர்புகளையும் ஆய்வு செய்வதால் இதன் பயன்பாடு விரிவடைந்துள்ளது.

8. இது அதிகம் மேற்கணக்கீட்டிற்கு பயன்படுத்தப்படுகின்றது.

இரு ஒட்டுறவுக் கோடுகள்

X சார்ந்த Y => X = a + by 

Y சார்ந்த X = > Y = a + bx

ஒரு மாறியின் மதிப்பை மற்றொரு மாறியின் மதிப்புக்கு மதிப்பீடு செய்யும் கோடே ஒட்டுறவுக் கோடாகும். இருமாறிகளுக்கிடையே உள்ள சராசரித் தொடர்பினை இக்கோடு கணித வடிவில் தருகின்றது. மற்றொரு மாறியின் குறிப்பிட்ட மதிப்பிற்கு ஒரு மாறியின் சிறந்த கணிப்பு மதிப்பை ஒட்டுறவுக் கோடுகள் தருகின்றது.

முந்தைய பகுதிகளில் கூட்டுச் சராசரி, திட்டவிலக்கம் மற்றும் உடன் தொடர்பு பற்றி படித்தோம். ஒட்டுறவுக்கோட்டுச் சமன்பாடுகள் பின்வருமாறு:

X இன் மதிப்பு Y இன் மதிப்பைச் சார்ந்த ஒட்டுறவுக் கோட்டுச் சமன்பாடு

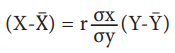
Y இன் மதிப்பு X இன் மதிப்பைச் சார்ந்த ஒட்டுறவுக் கோட்டுச் சமன்பாடு

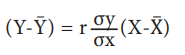
X இன் மதிப்பு Y இன் மதிப்பைச் சார்ந்த, Y இன் மதிப்பு X இன் மதிப்பைச் சார்ந்த ஒட்டுறவுக்கோடுகள் கீழ்க் கொடுக்கப்பட்டுள்ள உதாரணம் மூலம் விளக்கப்படுகின்றது.

உதாரணம் 10

கொடுக்கப்பட்டுள்ள விவரங்களிலிருந்து X மதிப்பு Y ஐச் சார்ந்த மற்றும் Y மதிப்பு X ஐச் சார்ந்த ஒட்டுறவுக் கோடுகளின் சமன்பாடு காண்.

X இன் மதிப்பு Y ஐச் சார்ந்த ஒட்டுறவுக் கோட்டின் சமன்பாடு

Y இன் மதிப்பு X ஐச் சார்ந்த ஒட்டுறவுக் கோட்டின் சமன்பாடு

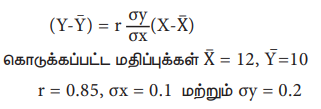
இந்த மதிப்புக்களை சூத்திரத்தில் பிரதியிட

(Y-10) = 0.85 (0.2/0.1) (X-12) 

(Y-10) = 0.85 (2) (X-12)

   Y = 1.7 x (X-12) + 10 

   Y = 1.7X-20.4+10 

   Y = 1.7X-10.4

விடை   Y = 1.7X-10.4

Y இன் மதிப்பு X ஐச் சார்ந்த ஒட்டுறவுக் கோட்டின் சமன்பாடு