வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் - திசையிலி முப்பெருக்கல் (Scalar triple product) | 12th Maths : UNIT 6 : Applications of Vector Algebra

12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்

திசையிலி முப்பெருக்கல் (Scalar triple product)

12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்

வரையறை 6.4

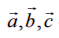என்பன கொடுக்கப்பட்ட மூன்று வெக்டர்கள் எனில், 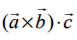என்பது அவ்வெக்டர்களின் திசையிலி முப்பெருக்கல் எனப்படும். 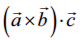ஒரு திசையிலியாகும்.

குறிப்புரை

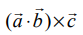(1) என்பது ஒரு திசையிலியாதலால் ஆனது பொருளற்றது.

(2) 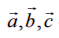என்பன கொடுக்கப்பட்ட மூன்று வெக்டர்கள் எனில், பின்வருவன அவற்றின் திசையிலி முப்பெருக்கல்கள் ஆகும்:

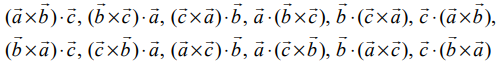
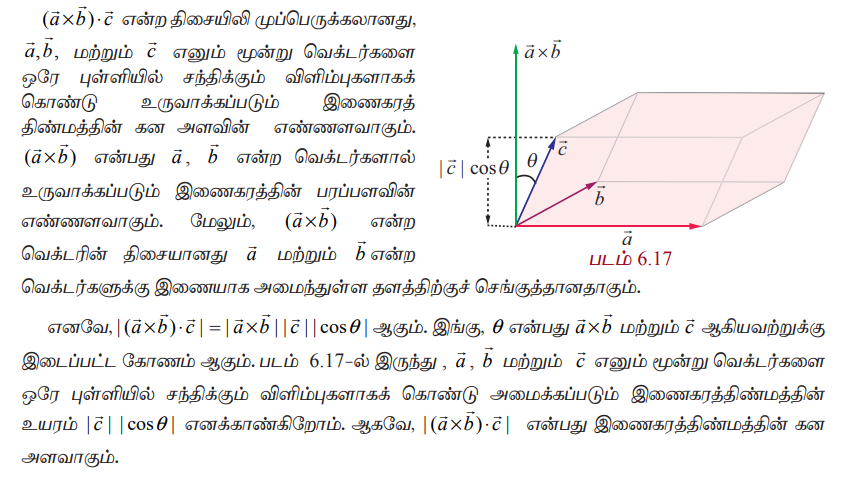
திசையிலி முப்பெருக்கலின் வடிவக்கணித விளக்கம் (Geometrical interpretation of scalar triple product)

திசையிலி முப்பெருக்கல்களைக் காண்பதற்கு பின்வரும் தேற்றம் பயன்படுகிறது.

தேற்றம் 6.1

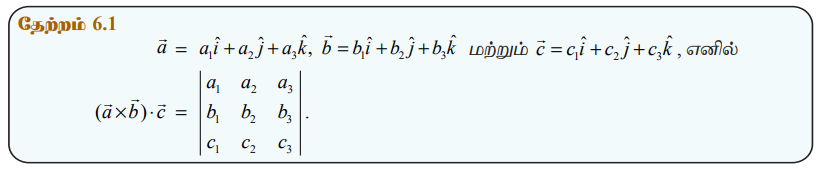
நிரூபணம்

திசையிலி முப்பெருக்கலின் வரையறைப்படி

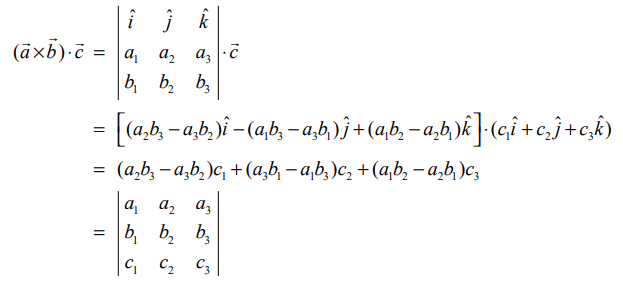
எனவே, தேற்றம்நிரூபிக்கப்பட்டது.

1. திசையிலி முப்பெருக்கலின் பண்புகள் (Properties of the scalar triple product)

தேற்றம் 6.2

எனவே, தேற்றம் நிரூபிக்கப்பட்டது.

குறிப்பு

தேற்றம் 6.2−ல் இருந்து, திசையிலிப் பெருக்கலில் வெக்டர் மற்றும் புள்ளிப் பெருக்கல் குறிகளை அடைப்புக் குறிகளுக்குள் உள்ள வெக்டர்களுக்கு இடையில் வெக்டர் பெருக்கல் குறியும் அடைப்புக் குறிக்கு வெளியே புள்ளிப் பெருக்கல் குறியும் இருக்குமாறு வெக்டர்கள் அமைந்துள்ள வரிசையை மாற்றாமல் இடமாற்றம் செய்யலாம். எடுத்துக்காட்டாக,

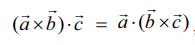ஏனெனில் ‘.' P மற்றும் × குறிகளை இடமாற்றம் செய்யலாம்

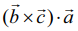= , திசையிலி பெருக்கலின் பரிமாற்றுப் பண்பு

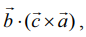= ஏனெனில் ‘.' மற்றும் × குறிகளை இடமாற்றம் செய்யலாம்

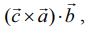= திசையிலி பெருக்கலின் பரிமாற்றுப் பண்பு

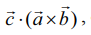= ஏனெனில் ‘.’ மற்றும் × குறிகளை இடமாற்றம் செய்யலாம்

குறியீடு

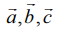என்பன ஏதேனும் மூன்று வெக்டர்கள் எனில், திசையிலி முப்பெருக்கல் 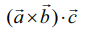என்பதை 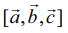எனக்குறிக்கிறோம்.

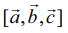என்பதை பெட்டி 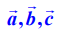எனப்படிக்கிறோம். திசையிலி முப்பெருக்கல் மதிப்பின் எண்ணளவு ஒரு பெட்டியின் (செவ்வக வடிவ இணைகரத்திண்மம்) கன அளவைக் குறிப்பதால், இப்பெருக்கல் பெட்டிப் பெருக்கல் எனவும் அழைக்கப்படுகிறது.

குறிப்பு

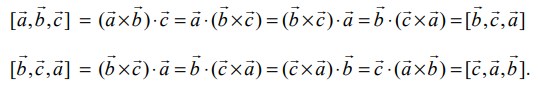
அதாவது, திசையிலி முப்பெருக்கலில் உள்ள வெக்டர்களை அதே வரிசையில் வட்டச் சுழற்சி முறையில் மாற்றம் செய்வதால், திசையிலி முப்பெருக்கலின் மதிப்பு மாறாது.

ஆகவே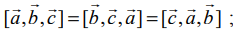

(2) திசையிலி முப்பெருக்கலில் உள்ள ஏதேனும் இரு வெக்டர்களை இடமாற்றம் செய்வதால், திசையிலி பெருக்கலின் மதிப்பானது (−1) −ஆல் பெருக்கப்படும். அதாவது,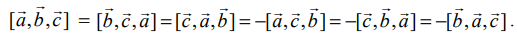

(3) (i) ஏதேனும் இரு வெக்டர்கள் சமம் எனில், திசையிலி முப்பெருக்கம் பூச்சியம் ஆகும். அதாவது, 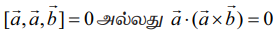ஆகும்.

(ii) ஏதேனும் இரு வெக்டர்கள் இணை எனில், திசையிலி முப்பெருக்கம் பூச்சியம் ஆகும்.

தேற்றம் 6.3

திசையிலி முப்பெருக்கல், வெக்டர் கூட்டல் மற்றும் திசையிலிப் பெருக்கல் ஆகியவற்றின் பண்புகளை நிறைவு செய்கிறது. அதாவது,

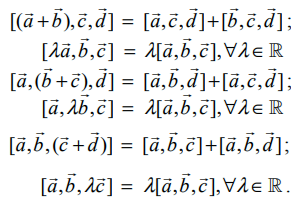
நிரூபணம்

திசையிலிப் பெருக்கல் மற்றும் வெக்டர் பெருக்கல் பண்புகளைப் பயன்படுத்த,

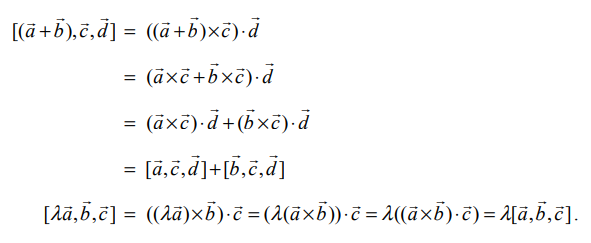
இத்தேற்றத்தின் முதல் முடிவினைப் பயன்படுத்தி, பின்வரும் முடிவுகளைப் பெறுகிறோம்

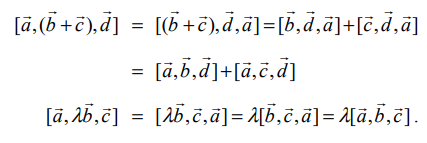
இதே போல், மற்ற சமன்பாடுகளையும் நிரூபிக்கலாம்.

பூச்சியமற்ற மூன்று வெக்டர்கள் ஒரு தள வெக்டர்கள் எனில், அவற்றில் ஏதேனும் ஒரு வெக்டரை மற்ற இரண்டு வெக்டர்களின் நேரியல் சேர்வாக எழுத முடியும் என பதினோராம் வகுப்பில் கற்றுள்ளோம். இப்பொழுது, ஒரு தள வெக்டர்களின் பண்புகளை திசையிலி முப்பெருக்கலைப் பயன்படுத்திக் காணலாம்.

தேற்றம் 6.4

பூச்சியமற்ற மூன்று வெக்டர்களின் திசையிலி முப்பெருக்கல் பூச்சியம் என இருந்தால், மட்டுமே அம்மூன்று வெக்டர்களும் ஒரு தள வெக்டர்களாகும்.

நிரூபணம்

தேற்றம் 6.5

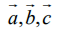என்ற மூன்று வெக்டர்கள் ஒரு தள வெக்டர்களாக இருக்கத் தேவையானதும் மற்றும் போதுமானதுமான நிபந்தனை குறைந்தபட்சம் ஒன்றாவது பூச்சியமற்றதாகவும் மற்றும் 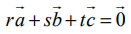என்றிருக்குமாறும் r, s, t ∈ ℝ என்ற திசையிலிகளைக் காணமுடியும் என்பதாகும்.

நிரூபணம்

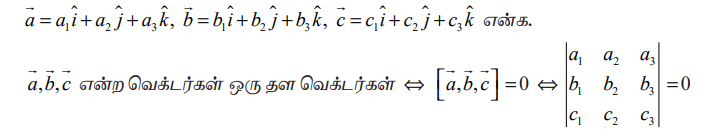
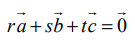⇔ என்றிருக்குமாறு குறைந்தபட்சம் ஒன்றாவது பூச்சியமற்றதாக உள்ள r, s, t ∈ ℝ என்ற திசையிலிகளைக் காண முடியும்.

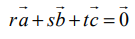⇔ என்றிருக்குமாறு குறைந்தபட்சம் ஒன்றாவது பூச்சியமற்றதாக உள்ள r, s, t ∈ ℝ என்ற திசையிலிகளை காணலாம்.

தேற்றம் 6.6

குறிப்பு

தேற்றம் 6.6ன்படி, 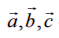என்பன ஒரு தளம் அமையா வெக்டர்கள் மற்றும் 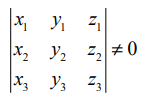எனில்,

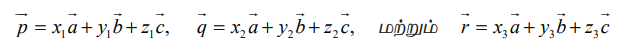எனும் மூன்று வெக்டர்களும் ஒரு தளம் அமையா வெக்டர்களாகும்.

எடுத்துக்காட்டு 6.12

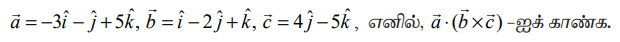
தீர்வு

மூன்று வெக்டர்களின் திசையிலி முப்பெருக்கலின் வரையறைப்படி,

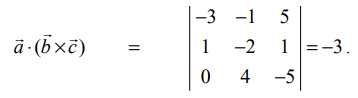
எடுத்துக்காட்டு 6.13

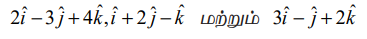என்ற வெக்டர்களை ஒரு முனையில் சந்திக்கும் விளிம்புகளாகக் கொண்ட இணைகரத் திண்மத்தின் கன அளவினைக் காண்க.

தீர்வு

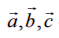என்ற வெக்டர்களை ஒரு புள்ளியில் சந்திக்கும் விளிம்புகளாகக் கொண்ட இணைகரத் திண்மத்தின் கன அளவு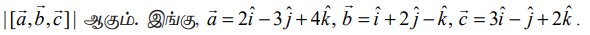

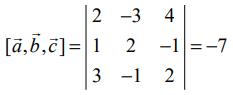என்பதால், இணைகரத் திண்மத்தின் கன அளவு 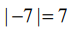கன அலகுகளாகும்.

எடுத்துக்காட்டு 6.14

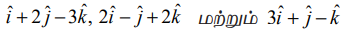ஆகிய வெக்டர்கள் ஒரு தள வெக்டர்களாகும் என நிரூபிக்க.

தீர்வு

இங்கு,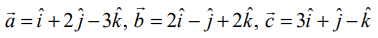

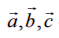என்ற வெக்டர்கள் ஒரு தள வெக்டர்களாகத் தேவையானதும் மற்றும் போதுமானதுமான நிபந்தனை 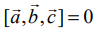ஆகும். இங்கு, 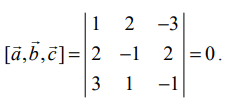எனவே, கொடுக்கப்பட்ட மூன்று வெக்டர்களும் ஒரு தள வெக்டர்களாகும்.

எடுத்துக்காட்டு 6.15

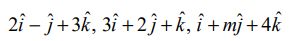என்ற வெக்டர்கள் ஒரு தள வெக்டர்கள் எனில், m−ன் மதிப்புக் காண்க.

தீர்வு

கொடுக்கப்பட்ட வெக்டர்கள் ஒரு தள வெக்டர்கள் என்பதால்,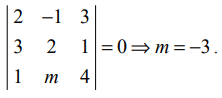

எடுத்துக்காட்டு 6.16

(6,–7,0), (16,−19,–4), (0,3,–6), (2,–5,10) என்ற நான்கு புள்ளிகளும் ஒரே தளத்தில் அமையும் என நிறுவுக.

தீர்வு

A = (6,−7,0), B = (16,−19,–4), C = (0,3,−6), D=(2,−5,10) என்க. A,B,C,D என்ற நான்கு புள்ளிகளும் ஒரே தளத்தில் அமையும் என நிரூபிக்க, 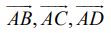என்ற மூன்று வெக்டர்கள் ஒரு தள வெக்டர்களாகும் என நிரூபிக்க வேண்டும்.

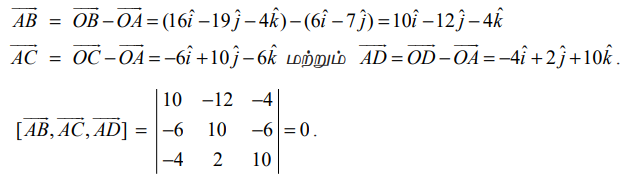
எனவே, 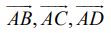என்ற வெக்டர்கள் ஒரு தள வெக்டர்களாகும். ஆகவே, A, B, C, மற்றும் D என்ற நான்கு புள்ளிகளும் ஒரே தளத்தில் அமைகின்றன.

எடுத்துக்காட்டு 6.17

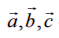என்ற வெக்டர்கள் ஒரு தள வெக்டர்கள் எனில், 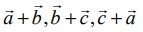என்ற வெக்டர்களும் ஒரு தள வெக்டர்களாகும் என நிறுவுக.

தீர்வு

எடுத்துக்காட்டு 6.18

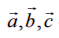என்பன மூன்று வெக்டர்கள் எனில் 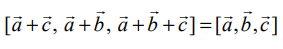என நிரூபிக்க.

தீர்வு

தேற்றம் 6.6−ஐபயன்படுத்தி இக்கணக்கினை நிரூபிக்கலாம்.

Tags : Definition, Properties, Theorem, Proof, Solved Example Problems, Solution வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள்.

12th Maths : UNIT 6 : Applications of Vector Algebra : Scalar triple product Definition, Properties, Theorem, Proof, Solved Example Problems, Solution in Tamil : 12th Standard Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் : திசையிலி முப்பெருக்கல் (Scalar triple product) - வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் : 12 ஆம் வகுப்பு புத்தகம் கேள்விகள் மற்றும் பதில்கள்.