இரு நேர்க்கோடுகளுக்கு இடைப்பட்ட மீச்சிறு தூரம் (Shortest distance between two straight lines)

6. இரு நேர்க்கோடுகளுக்கு இடைப்பட்ட மீச்சிறு தூரம் (Shortest distance between two straight lines)

இரு நேர்க்கோடுகளின் வெட்டும் புள்ளியை எவ்வாறு காண்பது எனவும் மற்றும் இரு கோடுகள் இணையானவையா இல்லையா என்பதை எவ்வாறு தீர்மானிப்பது எனவும் கற்றறிந்துள்ளோம்.

வரையறை 6.6

இரு நேர்க்கோடுகள் ஒரே தளத்தில் அமைந்தால், அவை ஒரு தளம் அமையும் கோடுகள் எனப்படும்.

குறிப்பு

இரு நேர்க்கோடுகள் இணைகோடுகளாகவோ அல்லது வெட்டும் கோடுகளாகவோ இருப்பின், அவை ஒரு தளம் அமையும் கோடுகளாகும்.

வரையறை 6.7

புற வெளியில் இணையாக இல்லாமலும் ஒன்றையொன்று வெட்டிக் கொள்ளாமலும் உள்ள இரு கோடுகளை ஒரு தளம் அமையாக் கோடுகள் என அழைக்கிறோம்.

குறிப்பு

இரு நேர்க்கோடுகள் ஒரு தளம் அமையாக் கோடுகள் எனில், அக்கோடுகள் ஒரே தளத்தில் இருக்காது.

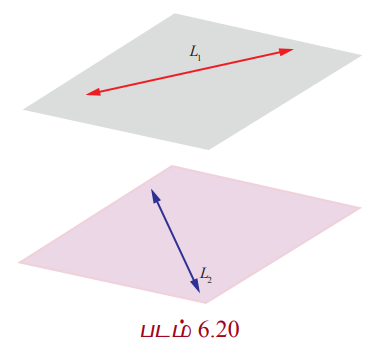
இணையாக இல்லாத இரண்டு நேர்க்கோடுகள் ஒன்றையொன்று வெட்டிக் கொண்டால், அக்கோடுகளுக்கு இடைப்பட்ட தூரம் பூச்சியம் ஆகும். ஒன்றையொன்று வெட்டாமலும் இணையாகவும் உள்ள இரண்டு நேர்க்கோடுகளுக்கு இடைப்பட்ட மீச்சிறு தூரமானது, இவ்விரு இணைக்கோடுகளுக்கும் செங்குத்தாக உள்ள கோட்டுத்துண்டின் நீளமாகும். இதேபோன்று, ஒரு தளம் அமையாக் கோடுகளுக்கு இடைப்பட்ட மீச்சிறு தூரமானது, ஒரு தளம் அமையாத இரு கோடுகளுக்கு செங்குத்தான கோட்டுத்துண்டின் நீளம் என வரையறுக்கப்படுகிறது. இரண்டு நேர்க்கோடுகள் இணைக்கோடுகளாகவோ அல்லது அமையாக் கோடுகளாகவோ இருக்கும்.

தேற்றம் 6.13

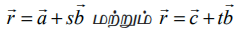என்ற இரண்டு இணைகோடுகளுக்கு இடைப்பட்ட மீச்சிறு தூரம்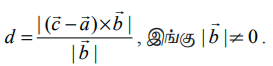

நிரூபணம்

கொடுக்கப்பட்ட 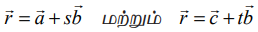என்ற இரண்டு இணைக்கோடுகளை முறையே L1 மற்றும் L2 எனக்குறிப்போம். L1 மற்றும் L2−களின் மீதுள்ள A மற்றும் B என்ற இரு புள்ளிகளின் நிலைவெக்டர்கள் முறையே மற்றும் என்க. கொடுக்கப்பட்ட இரு கோடுகளும் –க்கு இணையானவை.

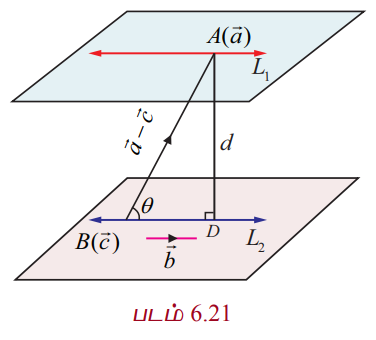
AD என்பது கொடுக்கப்பட்ட இரு கோடுகளுக்கும் செங்குத்து என்க. 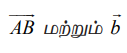என்ற வெக்டர்களுக்கு இடைப்பட்ட குறுங்கோணம் θ எனில்,

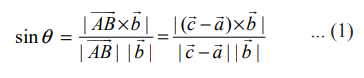
ஆனால், செங்கோண முக்கோணம் ABD−ல் இருந்து,

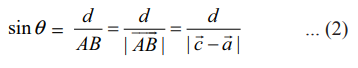
சமன்பாடுகள் (1) மற்றும் (2)−லிருந்து, நாம் பெறுவது

நிரூபணம்

கொடுக்கப்பட்ட 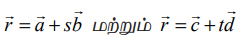என்ற ஒரு தளம் அமையாக் கோடுகளை முறையே L1 மற்றும் L2 எனக் குறிப்போம்.

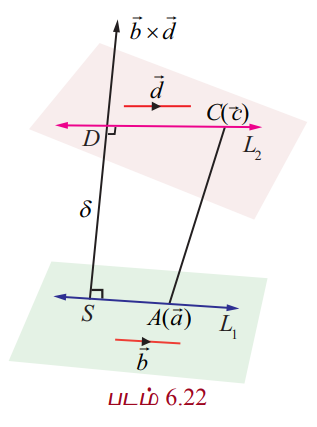
L1 மற்றும் L2 என்ற கோடுகளின் மீதுள்ள A மற்றும் C என்ற இரு புள்ளிகளின் நிலை வெக்டர்கள் முறையே 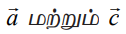என்க.

கொடுக்கப்பட்ட இரண்டு ஒரு தளம் அமையாக் கோடுகளின் சமன்பாடுகளிலிருந்து, L1 என்ற கோடு –க்கு இணையாகவும், L2 என்ற கோடு −க்கு இணையாகவும் இருப்பதைக் காண்கிறோம். ஆகையால், 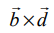என்பது L1 மற்றும் L1 என்ற இரண்டு கோடுகளுக்கும் செங்குத்தாகும்.

SD என்பது L1 மற்றும் L1 என்ற இரண்டு கோடுகளுக்கும் செங்குத்தாக உள்ள கோட்டுத்துண்டு என்க. ஆகவே ஆனது மற்றும் என்ற இரு வெக்டர்களுக்கும் செங்குத்தான வெக்டராகும். ஆதலால், 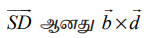−க்கு இணையான வெக்டராகும்.

எனவே, 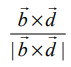என்பது  –ன் திசையில் உள்ள அலகு வெக்டராகும். மேலும், மீச்சிறு தூரம்

குறிப்புரை

(i) தேற்றம் 6.14−லிருந்து, 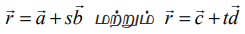என்பன ஒன்றையொன்று வெட்டும் கோடுகள் (அதாவது, ஒரு தளம் அமையும் கோடுகள்) எனில், 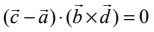ஆகும் எனக் காண்கிறோம்.

(2) 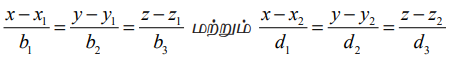என்ற கோடுகள் ஒன்றையொன்று வெட்டும் (அதாவது, ஒரு தளம் அமையும் கோடுகள்) எனில்,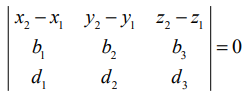

எடுத்துக்காட்டு 6.34

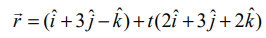மற்றும்  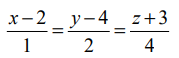 என்ற கோடுகள் வெட்டிக்கொள்ளும் புள்ளி வழியாகச் செல்வதும், மற்றும் இவ்விருகோடுகளுக்கும் செங்குத்தானதுமான நேர்க்கோட்டின் துணையலகு வெக்டர் சமன்பாட்டைக் காண்க.

தீர்வு

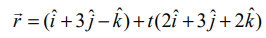என்ற கோட்டின் கார்டீசியன் சமன்பாடு  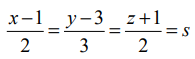 (என்க)

இக்கோட்டின் மீதுள்ள ஏதேனுமொரு புள்ளியின் அமைப்பு (2s +1, 3s+3, 2s−1)   …..(1)

இரண்டாவது கோட்டின் கார்டீசியன் சமன்பாடு 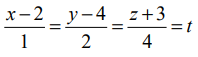(என்க)

இக்கோட்டின் மீதுள்ள ஏதேனுமொரு புள்ளியின் அமைப்பு (t+2, 2t+4, 4t−3)  …..(2)

கொடுக்கப்பட்ட கோடுகள் வெட்டிக் கொள்ளுமானால், ஒரு பொதுவான புள்ளி இருக்க வேண்டும். எனவே, ஒரு சில s, t ∈ ℝ களுக்கு,

 (2s +1, 3s +3, 2s−1) = (t+2, 2t + 4, 4t−3).

x,y மற்றும் z−ன் அச்சுத்தூரங்களை சமப்படுத்த, நாம்பெறுவது

2s−t=1, 3s−2t=1 மற்றும் s−2t=−1.

இம்மூன்று சமன்பாடுகளில் முதல் இரண்டு சமன்பாடுகளின் தீர்வு காண்பதால் s=1 மற்றும் t=1 எனக்கிடைக்கிறது. s மற்றும் t−ன்  இம்மதிப்புகள் மூன்றாவது சமன்பாட்டை நிறைவு செய்கின்றன. எனவே, கொடுக்கப்பட்ட கோடுகள் வெட்டும் கோடுகளாகும். இப்பொழுது, s –ன் மதிப்பை சமன்பாடு (1)−ல் அல்லது t –ன் மதிப்பை சமன்பாடு (2)−ல் பிரதியிட, இவ்விரு கோடுகளின் வெட்டும் புள்ளி (3,6,1) எனக் கிடைக்கிறது.

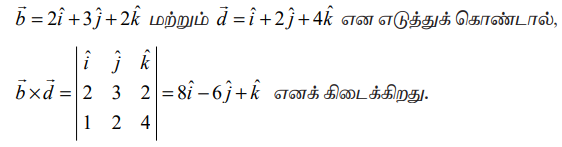
இவ் வெக்டர் கொடுக்கப்பட்ட இரு கோடுகளுக்கும் செங்குத்தான வெக்டராகும்.

எனவே, தேவையான நேர்க்கோடு (3,6,1) என்ற புள்ளி வழியாகச் செல்வதுடன் இரு நேர்க்கோடுகளுக்கும் செங்குத்தானதும் ஆகும். ஆகவே, தேவையான நேர்க்கோடு (3,6,1) என்ற புள்ளி வழியாகச் செல்வதுடன் 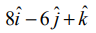என்ற வெக்டருக்கு இணையாகவும் இருக்கும். எனவே, தேவையான நேர்க்கோட்டின் வெக்டர் சமன்பாடு

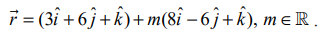
எடுத்துக்காட்டு 6.35

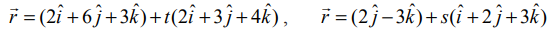என்ற ஒரு ஜோடி நேர்க்கோடுகள் இணைக்கோடுகளாகுமா எனக் காண்க. மேலும், அக்கோடுகளுக்கு இடைப்பட்ட மீச்சிறு தூரம் காண்க.

தீர்வு

கொடுக்கப்பட்ட இரு சமன்பாடுகளையும் 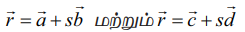உடன் ஒப்பிட்டு, நாம் பெறுவது  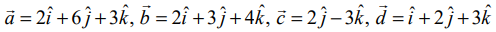 ஆகும்.

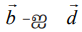–ன் திசையிலிப் பெருக்கலாக எழுத முடியாது என்பதை தெளிவாகக் காண்கிறோம். ஆகவே, இவ்விரு வெக்டர்கள் இணையான வெக்டர்கள் அல்ல. ஆதலால், இரு கோடுகளும் இணையான கோடுகள் அல்ல.

இரு கோடுகளுக்கு இடைப்பட்ட மீச்சிறு தூரம்

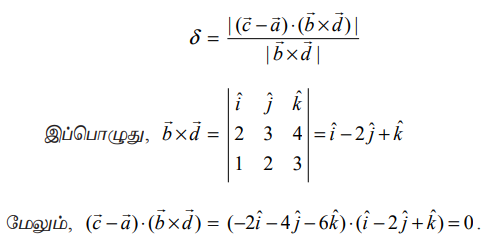
எனவே, இரு கோடுகளுக்கு இடைப்பட்ட மீச்சிறு தூரம் பூச்சியம் ஆகும். ஆகவே, கொடுக்கப்பட்ட கோடுகள் ஒன்றையொன்று வெட்டும் கோடுகளாகும்.

எடுத்துக்காட்டு 6.36

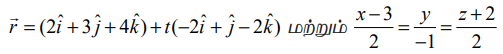என்ற கோடுகளுக்கு இடைப்பட்ட மீச்சிறு தூரம் காண்க.

தீர்வு

கொடுக்கப்பட்ட இரு கோடுகளின் துணையலகு வடிவ வெக்டர் சமன்பாடுகள் முறையே 

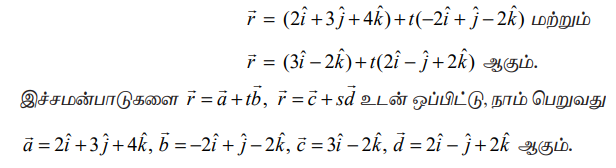
இங்கு 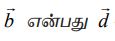−ன் திசையிலிப் பெருக்கலாக அமைந்துள்ளதைக் காண்கிறோம். ஆகவே, இவ்விரு கோடுகளும் இணையான கோடுகளாகும். இரண்டு இணையான நேர்க்கோடுகளுக்கு இடைப்பட்ட மீச்சிறு தூரம்

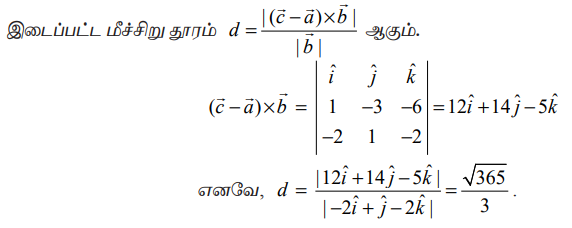
எடுத்துக்காட்டு 6.37

 (−1,2,3) என்ற புள்ளியிலிருந்து 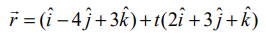என்ற நேர்க்கோட்டிற்கு வரையப்படும் செங்குத்தின் அடியின் அச்சுத்தூரங்களைக் காண்க. மேலும், கொடுக்கப்பட்ட புள்ளியிலிருந்து நேர்க்கோட்டிற்கு உள்ள மீச்சிறு தூரத்தைக் காண்க.

தீர்வு

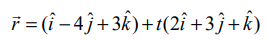என்ற சமன்பாட்டை 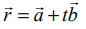உடன் ஒப்பிட்டு நாம் பெறுவது 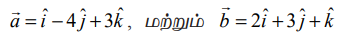ஆகும். கொடுக்கப்பட்ட (−1,2,3) என்ற புள்ளியை D எனவும், கோட்டின் மீதுள்ள (1,−4,3) என்ற புள்ளியை F எனவும் குறிக்கலாம். F என்பது D –யிலிருந்து கொடுக்கப்பட்ட நேர்க்கோட்டிற்கு வரையப்படும் செங்குத்துக் கோட்டின் அடி எனில், F என்ற புள்ளியின் அமைப்பு (2t+1, 3t−4, t+3) ஆகும். மேலும்,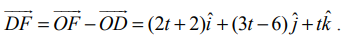

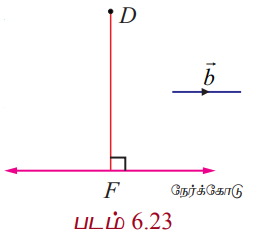
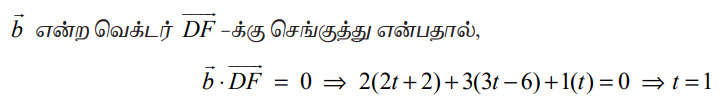
எனவே, F−ன் அச்சுத்தூரம் (3,−1,4) ஆகும்.

கொடுக்கப்பட்ட புள்ளியிலிருந்து கொடுக்கப்பட்ட கோட்டிற்கு உள்ள செங்குத்துத் தூரம் (மீச்சிறு தூரம்) 

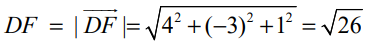அலகுகள்.