11வது இயற்பியல் : அலகு 7 : பருப்பொருளின் பண்புகள்
தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: மீட்சிக்குணகங்கள்
மூவகை மீட்சிக்குணகங்கள் உள்ளன.
(அ) யங் குணகம்
(ஆ) பருமக் குணகம்
(இ) விறைப்புக் குணகம் (அல்லது சறுக்குப்பெயர்ச்சிக் குணகம்)
(அ) யங் குணகம் (Young's modulus)
எடுத்துக்காட்டு 7.1
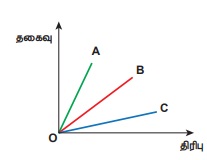
மீட்சி எல்லைக்குள் தகைவினால் A,B மற்றும் C என்ற கம்பிகளில் உருவான நீட்சித்திரிபுகள் படத்தில் காட்டப்பட்டுள்ளது. சமமான பளு செலுத்தப்பட்டதாகக் கொண்டு கம்பிப் பொருள்களின் மீட்சிப் பண்புகளை விவாதிக்கவும்.
மீட்சிக் குணகங்களை ஏறுவரிசையில் எழுதுக.
தீர்வு:
இங்கு மீட்சிக் குணகமானது யங் குணகம் ஆகும். நீட்சியின் காரணமாக தகைவு இழுவிசைத் தகைவாகவும் திரிபு இழுவிசைத் திரிபாகவும் உள்ளன.
மீட்சி எல்லைக்குள் தகைவானது திரிபுக்கு நேர்விகிதத்தில் உள்ளது (ஹூக் விதிக்கு உட்பட்டு) ஆகையால் வரைபடம் நேர்க்கோடாக உள்ளது. எனவே மீட்சிக்குணகத்தை (இங்கு யங் குணகம்) நேர்க்கோட்டிற்கு சாய்வு எடுப்பதன் மூலம் கணக்கிடலாம். சாய்வைக் கணக்கிட நாம் பெறுவது
A யின் சாய்வு > B யின் சாய்வு > C யின் சாய்வு இதன் மூலம் அறியப்படுவது,
C யின் யங் குணகம் < B யின் யங் குணகம் < A யின் யங் குணகம்
இங்கு சாய்வு அதிகமாக இருப்பின் திரிபு குறைவாக (நீளத்தில் சிறிய மாற்றம்) இருக்கும். பொருள் அதிக விறைப்பாக இருக்கும். எனவே, கம்பி A - இன் மீட்சிப்பண்பு ஆனது, கம்பி B மற்றும் கம்பி C இன், மீட்சிப்பண்பைவிட அதிகமாகவும் இருக்கும். இந்த உதாரணத்திலிருந்து நாம்புரிந்து கொள்வது யங்குணகம் என்பது திண்மப் பொருள் தனது நீளத்தை மாற்ற ஏற்படுத்தும் தடையின் அளவாகும்.
எடுத்துக்காட்டு 7.2
10 m நீளமுள்ள ஒரு கம்பியானது 1.25 × 10-4 m2 குறுக்குவெட்டுப் பரப்பைக் கொண்டுள்ளது. அது 5 kg பளுவிற்கு உட்படுத்தப்படுகிறது. கம்பிப் பொருளின் யங் குணகம் 4 × 1010 Nm-2 எனில் கம்பியில் உருவான நீட்சியைக் கணக்கிடுக (g = 10 ms-2 எனக் கொள்க)
தீர்வு
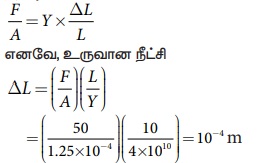
(ஆ) பருமக் குணகம் (Bulk modulus)
எடுத்துக்காட்டு 7.3
100 cm பக்கத்தைக் கொண்ட ஒரு உலோக கனசதுரம் அதன் முழு பக்கங்களிலும் செயல்படும் சீரான செங்குத்து விசைக்கு உட்படுத்தப்படுகிறது. அழுத்தம் 106 பாஸ்கல். பருமன் 1.5 × 10-5m3 என்ற அளவு மாறுபாடு அடைந்தால், பொருளின் பருமக்குணகத்தைக் கணக்கிடுக.
தீர்வு
வரையறைப்படி,
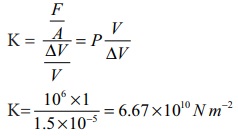
எடுத்துக்காட்டு 7.4
0.20 m பக்கத்தைக் கொண்ட ஒரு உலோக கனசதுரம் 4000 N சறுக்குப்பெயர்ச்சி விசைக்கு உட்படுத்தப்படுகிறது. மேற்பரப்பு அடிப்பரப்பைப் பொறுத்து 0.50 cm இடப்பெயர்ச்சி அடைகிறது. உலோகத்தின் சறுக்குப் பெயர்ச்சிக் குணகத்தைக் கணக்கிடுக.
தீர்வு
இங்கு L = 0.20 m, F = 4000 N, x = 0.50 cm = 0.005 m
மற்றும் பரப்பு A = L2 = 0.04 m2
எனவே,