பாகுநிலை

பாகுநிலை  (VISCOSITY)

அறிமுகம் 

பாடப்பகுதி 7.3 இல் ஓய்வில் உள்ள பாய்மங்களின் தன்மை குறித்து விவாதிக்கப்பட்டது. மாறுபட்ட பண்புகளில் பாய்ம இயக்கத்தின் தாக்கத்தை மேலும் விவாதிப்பதன் மூலம் வெளிக்கொணரலாம். ஒரு பாய்மத்தின் இயக்கம் சிக்கலான நிகழ்வாகும். ஏனென்றால் அது நிலை, இயக்க மற்றும் ஈர்ப்பு ஆற்றலைக் கொண்டு உராய்வை ஏற்படுத்தி பாகியல் விசைகளைத் தோற்றுவிக்கிறது. எனவே விவாதத்தை எளிமையாக்க ஒரு இலட்சிய திரவத்தின் நேர்வைக் கருதலாம். ஒரு இலட்சிய திரவமானது அமுக்க இயலாதது (அதாவது பருமக்குணகம் முடிவிலி) மற்றும் அதனுள் சறுக்குப்பெயர்ச்சி விசைகள் இருக்காது (அதாவது பாகியல் எண் சுழி). 

பெரும்பாலான பாய்மங்கள் இயக்கத்தை எதிர்க்கின்றன. ஒரு பாய்மம் ஒரு திண்மத்தைச் சார்ந்து இயங்கினால் அல்லது இரு பாய்மங்கள் ஒன்றுக்கொன்று சார்பு இயக்கத்தைக் கொண்டிருந்தால் நிலையான பரப்பில் ஒரு உராய்வு விசை செயல்படுகிறது. இந்த பாய்ம இயக்கத்தின் எதிர்ப்பானது ஒரு திண்மப்பொருள் ஒரு பரப்பில் இயங்கும் போது உருவாகும் உராய்வு விசையைப் போன்றது ஆகும். இயங்கும் பாய்ம ஏடுகளுக்கு இடையே தோன்றும் அக உராய்வு பாகுநிலை ஆகும். எனவே பாகுநிலையானது ஒரு பாய்மத்தின் ஏடுகளுக்கிடையே உள்ள சார்பு இயக்கத்தை எதிர்க்கும் பாய்மத்தின் பண்பு பாகுநிலை என வரையறுக்கப்படுகிறது.

செயல்பாடு

மூன்று உயரமான ஜாடிகளில் ஒரே அளவான மூன்று எஃகு பந்துகள் ஒரே நேரத்தில் விழச் செய்யப்படுகிறது. அது காற்றில் எளிதாக இயங்குகிறது ஆனால் நீரில் அவ்வளவு எளிதானதல்ல. எண்ணெயில் இயங்குவது இன்னும் கடினமானதாகும். விழும் பந்தினால் பாய்மத்தின் வெவ்வேறு ஏடுகளுக்கிடையே சார்பு இயக்கம் உருவாகி அதன் காரணமாக ஒரு விசை உருவாகிறது. இந்த உராய்வு விசை பாய்மத்தின் அடர்த்தியைச் சார்ந்தது. இயங்கும் பாய்மத்தின் ஏடுகளுக்கிடையே உள்ள சார்பு இயக்கத்தை எதிர்க்கும் பாய்மத்தின் பண்பு பாகுநிலை எனப்படும்.

பாகுநிலைக்கான காரணம் 

அருகில் அமைந்துள்ள இரு ஏடுகளைக் கொண்ட ஒரு திரவம் ஒரு கிடைமட்ட பரப்பில் பாய்வதாகக் கொள்க. மேல் ஏடானது கீழ் ஏட்டை முடுக்க முற்படும். அதைத் தொடர்ந்து கீழ் ஏடு மேல் ஏட்டை தடுக்க முற்படும். இதன் விளைவாக ஒரு பின்னோக்கிய தொடுவரை விசை தோன்றுகிறது. இது சார்பு இயக்கத்தைக் குலைக்கும். இதுவே பாய்மங்களின் பாகியல் தன்மைக்கான காரணமாகும்.

பாகியல் எண் (Coefficient of viscosity) 

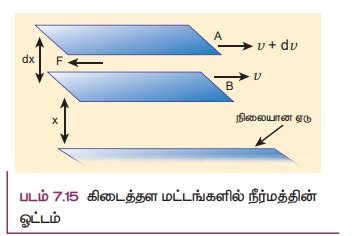
ஒரு நிலையான கிடைமட்ட ஏட்டின் மீது ஒரு திரவம் சீராகப் பாய்வதாகக் கொள்க (படம் 7.15) ஒரு நிலையான ஏட்டில் இருந்து தொலைவாகச் சென்றால் ஏடுகளின் வேகங்கள் சீராக அதிகரிக்கிறது. A மற்றும் B என்ற இரு இணையான ஏடுகளைக் கருதுக. நிலையான ஏட்டிலிருந்து x மற்றும் x + dx தொலைவில் அருகாமையில் உள்ள ஏடுகளின் திசைவேகங்கள் முறையே v மற்றும் v + dv எனக் கொள்க.

இரு ஏடுகளுக்கிடையே தொடுவரைத் திசையில் செயல்படும் பாகுநிலை விசை F ஆனது நியூட்டன் முதல் விதியின் மூலம் அறியப்படுகிறது. இந்த விசையானது (i) திரவத்தின் பரப்பு A மற்றும் (ii) திசைவேகச் சரிவு dv/dx ஆகியவற்றிற்கு நேர்விகிதத்தில் உள்ளது.

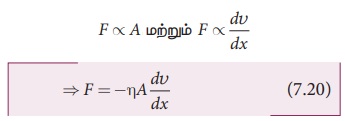
இங்கு விகித மாறிலி η திரவத்தின் பாகியல் எண் எனப்படும். எதிர்க்குறியானது விசை உராய்வுத் தன்மை கொண்டது மற்றும் அது சார்பு இயக்கத்தை எதிர்க்கிறது என்பதைக் குறிக்கிறது. பாகியல் எண்ணின் பரிமாணம் [ML− 1 T−1] ஆகும்.

குறிப்பு

பாகுநிலையானது உராய்வைப் போன்றதாகும். பொருளின் இயக்க ஆற்றல் வெப்ப ஆற்றலாக வெளிப்படுகிறது.

எடுத்துக்காட்டு 7.9

2.5×10-4m2 பரப்புள்ள ஒரு உலோகத்தட்டு 0.25×10-3m தடிமமான விளக்கெண்ணெய் ஏட்டின் மீது வைக்கப்பட்டுள்ளது. தட்டை 3×10-2m s-1, திசைவேகத்தில் நகர்த்த 2.5 N விசை தேவைப்பட்டால், விளக்கெண்ணெயின் பாகியல் எண்ணைக் கணக்கிடுக. கொடுக்கப்பட்டவை : 

A=2.5×10-4 m2, dx = 0.25×10-3m, 

F=2.5N and dv = 3×10-2 m s-1

தீர்வு

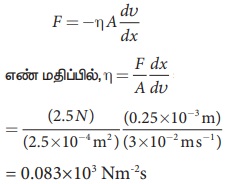
வரிச்சீர் ஓட்டம் (Streamlined flow)

பாய்மங்களின் ஓட்டம் மாறுபட்ட வகைகளில் உள்ளன. அது சீரான அல்லது வரிச்சீர் ஓட்டம், சீரற்ற அல்லது சுழற்சி ஓட்டம், அமுக்க இயலும் அல்லது அமுக்க இயலாத ஓட்டம், பாகியல் ஓட்டம் அல்லது பாகியலற்ற ஓட்டமாக இருக்கலாம். உதாரணமாக, ஒரு ஆற்றில் அமைதியாகச் செல்லும் நீரின் ஓட்டத்தைக் கருதுக. உற்று நோக்கினால் ஆற்றின் வெவ்வேறு இடங்களில் நீரின் திசைவேகம் மாறுபட்டுள்ளதை அறியலாம். அது ஆற்றின் நடுப்பகுதியில் வேகமானதாகவும், அதன் கரையோரங்களில் மெதுவானதாகவும் உள்ளது. எனினும் எந்த ஒரு புள்ளியிலும் நீர்மத்துகளின் திசைவேகம் மாறிலி ஆகும். புரிதலுக்காக, ஆற்றில் நடுப்பகுதியில் துகளின் திசைவேகம் வினாடிக்கு 4 மீட்டர் இருப்பதாகக் கருதுக. எனவே இந்தப் புள்ளியைக் கடக்கும் அனைத்துத் துகள்களின் திசைவேகங்களும் அதே மதிப்பைப் பெறும். இதுபோன்றே, கரையோரத்தில் பாயும் நீர்மத்துக்களின் திசைவேகம் வினாடிக்கு 0.5 மீட்டர் எனில் அதனைப் பின் தொடரும் அனைத்து நீர்மத்துகள்களின் திசைவேகங்களும் அதே மதிப்பைப் பெறும். 

ஒரு திரவ ஓட்டத்தில், ஒரு புள்ளியின் வழியே செல்லும் ஒவ்வொரு திரவத்துக்களும் அதற்கு முன்னர் சென்ற துகள்களின் பாதையிலேயே அதே திசைவேகத்தில் இயங்கினால் அந்த திரவ ஓட்டமானது வரிச்சீர் ஓட்டம் எனப்படும். இதனை சீரான ஓட்டம் அல்லது அடுக்குமுறை ஓட்டம் (Laminar flow) எனவும் குறிப்பிடலாம். இயங்கும் பாய்மத்துக்கள் மேற்கொள்ளும் வளைவானபாதை வரிச்சீர் எனப்படுகிறது. படம் 7.16 இல் காட்டியுள்ளவாறு எந்த ஒரு புள்ளியிலும் அதன் தொடுகோடானது அந்தப்புள்ளியில் பாய்ம ஓட்டத்தின் திசையைக் கொடுக்கிறது. இதனை இவ்வாறு அழைப்பதற்குக் காரணம் இது ஒரு நீர் ஓடை அல்லது இலட்சிய நிலையில் உள்ள ஆற்றைப் போன்று உள்ளதே ஆகும்.

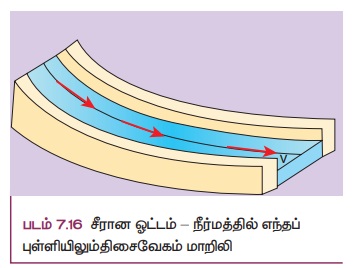
நீர்ம ஓட்டத்தின் திசைக்கு செங்குத்தான எந்த ஒரு குறுக்குவெட்டு பரப்பிலும் ஒரே திசைவேகத்தைக் கொண்ட சீரான வரிக் கற்றையைக் கருதினால் அந்த கற்றை குழாய் வடிவ ஓட்டம் (tube of flow) எனப்படும். குழாய் வடிவ ஓட்டத்தில் உள்ள எந்த ஒரு நீர்மத்துகளும் அதன் இயக்கம் முழுவதற்கும் குழாயினுள்ளேயே எப்போதும் இருக்கும் மற்றும் மற்ற குழாய் திரவத்துடன் கலக்காது என்பதை முக்கியமாக கவனிக்க வேண்டும். குழாய் வடிவ ஓட்டத்தின் அச்சு எப்போதும் வரிச்சீர் ஓட்டத்தைத் தரும். வரிச்சீர் ஓட்டங்கள் எப்போதும் பாய்மத்துகள்களின் இயக்கப் பாதைகளைக் குறிக்கின்றன. மாறுநிலைத் திசைவேகம் எனப்படும் ஒரு குறிப்பிட்ட திசைவேகம் வரை பாய்மத்தின் ஓட்டம் வரிச்சீராக உள்ளது. இதன் பொருள், மாறுநிலைத் திசைவேகத்திற்குக் குறைவான வேகத்தில் பாயும் போது வரிச்சீர் ஓட்டத்தைப் பெறலாம்.

சுழற்சி ஓட்டம் (Turbulent flow) 

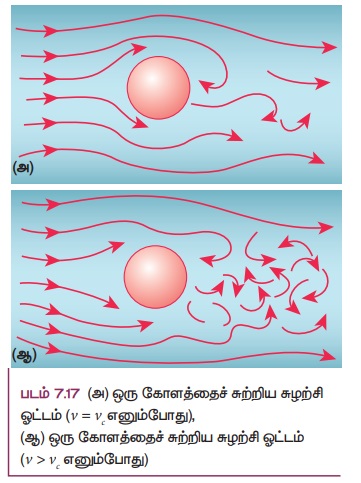
இயங்கும் பாய்மத்தின் வேகம் மாறுநிலைத் திசைவேகத்தை (vc) விட அதிகமானால் இயக்கமானது சுழற்சி ஓட்டமாகிறது. இந்நேர்வில் ஒவ்வொரு துகளிலும் திசைவேகமானது எண்மதிப்பிலும்,திசையிலும் மாறுவதால் தனிப்பட்ட துகள்கள் வரிச்சீர் ஓட்டத்தில் இயங்காது. எனவே சுழற்சி ஓட்டத்தில் துகள்களின் பாதை ஒழுங்கற்றதாக மாறி சுழல் ஓட்டம் அல்லது சுழல் எனப்படும் வட்டங்களில் இயங்கும். (படம் 7.17 (அ) மற்றும் (ஆ) ஒரு படகின் அல்லது கப்பலின் பின்புறமுள்ள நீரின் ஓட்டம் மற்றும் இயங்கும் பேருந்தின் பின்புறமுள்ள காற்று ஓட்டம் ஆகியவை சுழற்சி ஓட்டத்திற்குச் சில எடுத்துக்காட்டுகள் ஆகும்.

இரு வகையான இயக்கத்தின் வேறுபாட்டினை ஒரு அகன்ற குழாயில் பாயும் நீரினுள் அதன் அச்சின் வழியே ஒரு துளை மூலம் மையை செலுத்துவதன் மூலம் எளிதாக விளக்கலாம். பாய்மத்தின் திசைவேகம் குறைவாக உள்ள போது மை நேர்க்கோட்டுப் பாதையில் செல்லும். மாறாக திசைவேகமானது ஒரு குறிப்பிட்ட மதிப்பைவிட அதிமானால் மையானது பரவி ஒழுங்கற்ற இயக்கத்தைக் காட்டும். எனவே இயக்கமானது சுழற்சி ஓட்டமாக மாறுகிறது. வளைந்து நெளிந்து செல்லும் இயக்கத்தினால் சுழல் ஓட்டம் உருவாகி அதன் விளைவாக அதிக ஆற்றல் அழிக்கப்படுகிறது.

ரெனால்டு எண் 

ஒரு பாய்மத்தின் ஓட்டம் அதன்திசைவேகம் மாறுநிலைத் திசைவேகத்தை (vc) விட குறைவாக இருப்பின் சீரான அல்லது அடுக்குமுறை ஓட்டமாக உள்ளது. இல்லையெனில் ஓட்டம் சுழற்சி ஓட்டமாக மாறுகிறது என்பதை நாம் அறிந்து கொண்டோம். ஆஸ்போர்ன் ரெனால்டு (1842 - 1912) என்பவர் பாய்ம ஓட்டத்தின் தன்மையை அது வரிச்சீர் அல்லது சுழற்சி ஓட்டம் என அறிந்து கொள்ள ஒரு சமன்பாட்டை வடிவமைத்தார்.

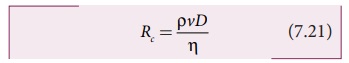
ரெனால்டு எண் எனப்படும் இது ஒரு பரிமாணமற்ற எண் ஆகும். இது Rc அல்லது K என்ற குறியீட்டால் குறிப்பிடப்படுகிறது. சமன்பாட்டில் ρ என்பது பாய்மத்தின் அடர்த்தி, v என்பது இயங்கும் பாய்மத்தின் திசைவேகம், D என்பது பாய்மம் செல்லும் குழாயின் விட்டம் மற்றும் η என்பது பாகியல் எண் ஆகியவற்றைக் குறிக்கின்றன. எந்த அலகு முறையிலும் Rc ஒரே மதிப்பைக் கொண்டிருக்கும்.

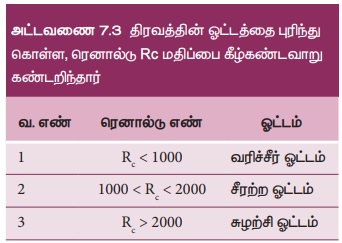
எனவே, ரெனால்டு எண் Rc என்பது ஒரு உருளை வடிவ குழாயின் வழியே செல்லும் பாய்மத்தின் ஓட்டம் வரிச்சீர் ஓட்டமா அல்லது சுழற்சி ஓட்டமா என முடிவு செய்யக்கூடிய ஒரு முக்கியமான மாறி ஆகும். 

உண்மையில், சுழற்சி ஓட்டம் தொடங்கும் Rc இன் மாறுநிலை மதிப்பு வடிவியலாக ஒரே மாதிரியுள்ள ஓட்டங்களுக்கு சமமான மதிப்பைக் கொண்டுள்ளது. உதாரணமாக மாறுபட்ட அடர்த்திகள் மற்றும் பாகியல் எண்கள் மதிப்புள்ள இரு திரவங்கள் (எண்ணெய் மற்றும் நீர்) சம வடிவம் மற்றும் அளவுகளைக் கொண்ட இரு குழாய்கள் வழியே சென்றால், ஒரே Rc மதிப்பில் சுழற்சி ஓட்டம் தொடங்குகிறது. மேற்கண்ட கருத்திலிருந்து ஒற்றுமை விதியைப் பெறலாம். அதன் கூற்றானது, இரு வடிவியல் ரீதியாக ஒரே மாதிரியான பாய்ம ஓட்டங்கள் இருந்தால் அவை இரண்டும் ஒரே ரெனால்டு எண்ணைக் கொண்டிருக்கும் வரை அடிப்படையில் ஒன்றுக்கொன்று சமமானதாகும். தொழில்நுட்ப பயன்பாடுகளில் ஒற்றுமை விதி முக்கிய பங்காற்றுகிறது. கப்பல்கள், நீர்மூழ்கி கப்பல்கள், பந்தயக்கார்கள் மற்றும் விமானங்களின் வடிவங்கள் அவற்றின் வேகம் பெரும் மதிப்பைப் பெறும் வகையில் வடிவமைக்கப்படுகின்றன.

முற்றுத்திசைவேகம் (Terminal Velocity)

முற்றுத்திசைவேகத்தைப் புரிந்து கொள்ள, ஒரு அதிக பாகுநிலை கொண்ட நீண்ட பாய்மத்தம்பத்தில் ஒரு சிறிய உலோகக் கோளம் ஓய்வு நிலையிலிருந்து தானே விழுவதாகக்கருதுக. கோளத்தின் மீது (i) செங்குத்தாக கீழ்நோக்கி செயல்படும் கோளத்தின் மீதான புவியீர்ப்பு விசை (ii) மிதக்கும் தன்மை காரணமாக மேல்நோக்கிய உந்து விசை U மற்றும் (iii) மேல்நோக்கி செயல்படும் பாகியல் விசை (பாகியல் விசை எப்போதும் கோளத்தின் இயக்கத்திற்கு எதிர்திசையில் செயல்படும்) ஆகிய விசைகள் செயல்படுகின்றன.

தொடக்கத்தில் மேல்நோக்கிய விசையானது, கீழ்நோக்கிய விசையை விட குறைவாக உள்ளதால் கோளம் கீழ்நோக்கிய திசையில் முடுக்கமடைகிறது. கோளத்தின் திசைவேகம் அதிகரித்தால் பாகியல் விசையும் அதிகரிக்கிறது. ஒரு கட்டத்தில் கீழ்நோக்கிய நிகர விசை மேல்நோக்கிய விசையை சமன்படுத்துவதால் கோளத்தின் மீதான தொகுபயன் விசை சுழியாகிறது. கோளம் தற்போது மாறா திசைவேகத்துடன் இயங்குகிறது.

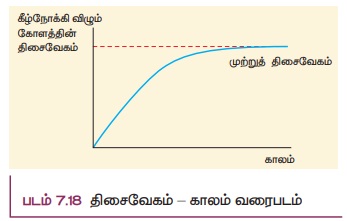
ஒரு பாகுநிலை ஊடகத்தின் வழியே தானே விழும் ஒரு பொருளானது அடையும் பெரும் மாறா திசைவேகம் முற்றுத்திசைவேகம் (vt) எனப்படும். படம் 7.18 இல் திசைவேகத்தை Y- அச்சிலும், காலத்தை X அச்சிலும் கொண்டு ஒரு வரைப்படம் வரையப்பட்டுள்ளது. 

கோளகமானது தொடக்கத்தில் முடுக்கமடைகிறது மற்றும் சிறிது நேரத்தில் அது மாறா மதிப்புள்ள முற்றுத்திசைவேகம் (vt) அடைகிறது என வரைபடத்திலிருந்து தெளிவாகிறது.

முற்றுத்திசைவேகத்திற்கான கோவை :

η பாகியல் எண் கொண்ட அதிக பாகுநிலையுள்ள திரவத்தின் வழியே ஆரமுள்ள r கோளம் ஒன்று விழுவதாகக் கருதுக. கோளப்பொருளின் அடர்த்தி ρ எனவும் பாய்மத்தின் அடர்த்தி σ எனவும் கொள்க.

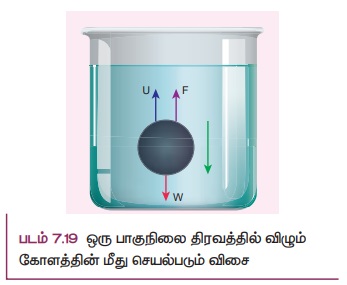
கோளத்தின் மீது செயல்படும் புவியீர்ப்பு விசை 

vt முற்றுத்திசைவேகத்தில் பாகியல் விசை

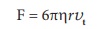
தற்போது, கீழ்நோக்கிய நிகர விசை மேல்நோக்கிய விசைக்கு சமமாகும்.

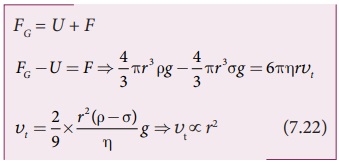
இங்கு கவனிக்க வேண்டியது, கோளத்தின் முற்றுத் திசைவேகம் அதன் ஆரத்தின் இருமடிக்கு நேர்த்தகவில் உள்ளது.

ρ ஐ விட σ அதிகமெனில், (ρ - σ) ஆனது எதிர்க்குறி மதிப்பபைப் பெறுவதால் முற்றுத்திசைவேகம் எதிர்க்குறியாகிறது. அதனால் தான் நீர் அல்லது எந்த திரவத்தின் வழியாகவும் காற்றுக்குமிழிகள் மேல்நோக்கி எழுகிறது. வானத்தில் மேகங்கள் மேல் நோக்கிய திசையில் நகருவதற்கும் இதுவே காரணமாகும்.

கவனத்தில் கொள்ள வேண்டியவை

i) ஒரு கோளத்தின் முற்றுத்திசைவேகம் கோளத்தின் ஆரத்தின் இருமடிக்கு நேர்த்தகவில் உள்ளது. எனவே, சிறிய மழைத்துளிகளை விடபெரிய மழைத்துளிகள் அதிக வேகத்துடன் விழுகின்றன. 

ii) கோள பொருளின் அடர்த்தி ஊடகத்தின் அடர்த்தியைவிட குறைவாக இருப்பின், கோளகமானது மேல்நோக்கிய திசையில் முற்றுத்திசைவேகத்தை அடைகிறது. அதனால் தான் சோடா நீரில் காற்றுக் குமிழிகள் மேல்நோக்கி எழுகின்றன.

ஸ்டோக் விதி மற்றும் அதன் பயன்பாடுகள்

பாகுநிலை ஊடகத்தின் வழியே ஒரு பொருள் வீழ்ந்தால் அதனுடன் உடனடியாக தொடுதலில் உள்ள பாய்ம ஏட்டை அது இழுக்கும். இது திரவத்தின் வெவ்வேறு ஏடுகளுக்கு இடையே சார்பு இயக்கத்தை உருவாக்குகிறது. ஸ்டோக் வெவ்வேறு பாய்மங்களில் சிறிய கோளப்பொருள்களின் இயக்கத்திற்கான பல சோதனைகள் செய்து, r ஆரமுள்ள கோளப்பொருளின் மீது செயல்படும் பாகியல் விசை F ஆனது

i) கோளத்தின் ஆரம் (r) 

ii) கோளத்தின் திசைவேகம் (v) மற்றும்

iii) திரவத்தின் பாகியல் எண் η

ஆகியவற்றைச் சார்ந்தது என்ற முடிவைப் பெற்றார். எனவே F ∝ ηx r yvz ⇒ F =kηxr y vz இங்கு k என்பது ஒரு பரிமாணமற்ற மாறிலி

பரிமாணங்களைப் பயன்படுத்தி, மேற்கண்ட சமன்பாட்டை இவ்வாறு எழுதலாம்.

[MLT – 2]  = k [ML−1T – 1] x ×[ L]y × [LT−1] z 

தீர்வு காண, x = 1, y = 1 மற்றும் z = 1 எனவே F=kη rv

சோதனைமூலம் k = 6π என ஸ்டோக் கண்டறிந்தார்.

இந்த தொடர்பு ஸ்டோக் விதி எனப்படும்.

ஸ்டோக் விதியின் செயல்முறைப் பயன்பாடுகள் : 

மழைத்துளிகள் அளவில் சிறியதாகவும், அதன் முற்றுத்திசைவேகங்கள் குறைவாகவும் உள்ளதால் அவை மேக வடிவில் காற்றில் மிதக்கின்றன. அவை அளவில் பெரிதாகும் போது அவற்றின் முற்றுத்திசைவேகங்கள் அதிகரித்து மழையாக கீழே விழுகின்றன. 

இந்த விதி கீழ்க்காண்பவற்றை விளக்குகிறது : 

அ) மேகங்களின் மிதத்தல் 

ஆ) சிறிய மழைத்துளிகளைவிட பெரிய மழைத்துளிகள் நம்மை அதிகமாக தாக்குகின்றன

இ) பாராசூட் உதவியுடன் கீழிறங்கும் ஒருவர் மாறா முற்றுத்திசைவேகத்தை பெறுகின்றார்.

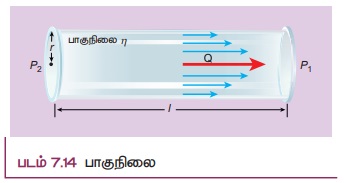
பாய்ஸன் சமன்பாடு (Poiseuille's equation)

ப்வாய்சொய் ஒரு நுண்குழாய் வழியே திரவத்தின் சீரான ஓட்டத்தை பகுப்பாய்வு செய்தார். அவர் நுண்குழாய் வழியாக ஒரு நொடியில் பாயும் திரவத்தின் பருமனுக்கான சமன்பாட்டைத் தருவித்தார். 

அவரது கருத்தின்படி சமன்பாட்டைத் தருவிக்க கீழ்க்காணும் நிபந்தனைகளைக் கருத்தில் கொள்ள வேண்டும்.

• குழாயின் வழியே திரவத்தின் ஓட்டம் வரிச்சீர் ஓட்டமாக இருக்க வேண்டும். 

• குழாய் கிடைமட்டமாக புவிஈர்ப்புவிசை நீர்ம ஓட்டத்தைப் பாதிக்காதவாறு இருக்க வேண்டும். 

• குழாயின் சுவரைத் தொடும் நீர்ம ஏடு ஓய்வில் இருக்க வேண்டும். 

• குழாயின் எந்த குறுக்குப்பரப்பிலும் அழுத்தம் சீராக இருக்க வேண்டும். 

பரிமாணப்பகுப்பாய்வை பயன்படுத்தி நாம் ப்வாய் சொய் சமன்பாட்டைத் தருவிக்கலாம். கிடைமட்டமாக உள்ள நுண் குழாயின் வழியே ஒரு திரவம் சீராக பாய்வதாகக் கருதுக. நுண் குழாயிலிருந்து ஒரு நொடியில் வெளியேறும் திரவத்தின் பருமன் v=(V/t) எனக் கொள்க. அது (அ) திரவத்தின் பாகியல் எண் (η) (ஆ) குழாயின் ஆரம் (r) மற்றும் (இ) அழுத்தச்சரிவு (P/l) ஆகியவற்றைச் சார்ந்தது.

இங்கு k என்பது ஒரு பரிமாணமற்ற மாறிலி.

எனவே 

எனவே M, L, மற்றும் T இன் அடுக்குகளை இருபுறமும் சமப்படுத்த

a + c = 0, −a + b −2c =3, மற்றும் −a −2c = −1 

a, b, மற்றும் c ஆகிய தெரியாத மதிப்புகள் உள்ளன. மூன்று சமன்பாடுகளைத் தீர்வு காண நாம் பெறுவது 

a = −1, b = 4, மற்றும் c = 1 எனவே சமன்பாடு (7.24) ஆனது,

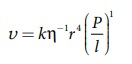
சோதனை மூலம் K – இன் மதிப்பு π / 8 , என காணப்பட்டது. எனவே,

மேற்கண்ட சமன்பாடு குறுகிய குழாய் அல்லது நுண்குழாய் வழியே செல்லும் நீர்ம ஓட்டத்திற்கே பொருந்தும். இச்சமன்பாடு ப்வாய்சொய் சமன்பாடு எனப்படும். இந்த தொடர்பானது மாறுநிலைத் திசைவேகத்தை (vc) விட குறைவான திசைவேகம் கொண்ட பாய்மங்களுக்கு நன்கு பொருந்துகின்றது.

பாகுநிலையின் பயன்பாடுகள் 

பாகுநிலையின் முக்கியத்துவத்தை கீழ்க்காணும் உதாரணங்களில் இருந்து புரிந்து கொள்ளலாம். 

1. கனரக இயந்திரங்களின் பாகங்களில் உயவியாகப் பயன்படும் எண்ணெய் அதிக பாகியல் எண்ணைக் கொண்டிருக்க வேண்டும். பொருத்தமான உயவியைத் தேர்வு செய்ய அதன் பாகுநிலையையும், அது வெப்பநிலையைப் பொறுத்து எவ்வாறு மாறுபாடுகிறது என்பதையும் அறிந்திருக்க வேண்டும். 

[குறிப்பு: வெப்பநிலை உயர்ந்தால் திரவத்தின் பாகுநிலை குறைகின்றது]. மேலும் கார் இயந்திரங்களில் (இலகுரக இயந்திரம்) பயன்படும் குறைந்த பாகுநிலையுள்ள எண்ணெய்களைத் தேர்வு செய்யவும் இது உதவுகிறது. 

2. சில கருவிகளின் இயக்கத்திற்கு ஈரப்பதத்தைக் கொடுக்க அதிக பாகுநிலை கொண்ட திரவம் பயன்படுத்தப்படுகிறது மற்றும் அது நீரியல் தடுப்பிகளில் (hydraulic brakes) தடுப்பி எண்ணெய்யாக பயன்படுகிறது. 

3. தமனிகள் மற்றும் இரத்தக் குழாய்கள் வழியே இரத்த ஓட்டம் நீர்மத்தின் பாகுநிலையைச் சார்ந்தது. 

4. ஒரு எலக்ட்ரானின் மின்னூட்டத்தைக் காண மில்லிகன் எண்ணெய்த் துளி ஆய்வை மேற்கொண்டார். அவர் பாகுநிலை பற்றிய அறிவை மின்னூட்டத்தைக் கணக்கிட பயன்படுத்தினார்.