முறுடுகள் (Surds)

முறுடுகள் (Surds)

மெய்யெண்களைப் பற்றிய கருத்துகள், அவற்றை எண்கோட்டில் குறித்தல் மற்றும் கையாளுதல் ஆகியவற்றை நன்கு அறிந்த நாம் தற்போது குறிப்பிட்ட சில தோராய மதிப்புகளை எப்படி முறுடுகளாக தனித்துவமான முறையில் குறிப்பிடுவது என்பது பற்றி கற்க இருக்கின்றோம்.

 √4 என்ற எண்ணை √ குறியீடு இல்லாமல் நம்மால் சுருக்கமாகக் கூற இயலுமா? ஆம் முடியும். √4 இக்குப் பதிலாக 2 என எளிமையாக எழுத முடியும். அப்படியானால், √[1/9] யும் அவ்வாறே எழுதலாமா? மிகவும் எளிதாக எழுதலாம். √ குறியீடு இல்லாமல் இதன் மதிப்பு 1/3 ஆகும். √0.01 இன் மதிப்பு என்ன? இதனையும் எளிதாக எழுதலாம். இதன் தீர்வு 0.1 ஆகும்.

√4, √1/9 மற்றும் √0.01 என்பவற்றின் தீர்வு காணும்போது √ குறியீடு இல்லாமல் இருப்பதை நம்மால் காண முடிகிறது. எல்லா இடங்களிலும் இவ்வாறு செய்ய இயலுமா? √18 என்பதைக் கருதுக. மூலக்குறியீடு இல்லாமல் இதன் மதிப்பை நம்மால் காண இயலுமா? 2−ன் வர்க்கமூலம், 5−ன் கனமூலம் போன்று மூலக்குறியீடு இல்லாமல் தீர்வு காண இயலாத எண்கள் முறுடுகள் எனப்படுகின்றன. அவை விகிதமுறு எண்களைக் கெழுக்களாகக் கொண்ட சமன்பாட்டின் விகிதமுறா மூலங்கள் ஆகும். 

முறுடு என்பது ஒரு விகிதமுறு எண்ணின் விகிதமுறா மூலம் ஆகும். n√a என்பது ஒரு முறுடு, இங்கே n ∈ ℕ, n>1, 'a' ஒரு விகிதமுறு எண்.

எடுத்துக்காட்டுகள்: √2 ஒரு முறுடு. இது x2 = 2 என்ற சமன்பாட்டின் விகிதமுறா மூலம் ஆகும். (x2 − 2 = 0 என்பது விகிதமுறு எண்களைக் கெழுக்களாகக் கொண்ட சமன்பாடு என்பதைக் கவனிக்க. √2 என்பது விகிதமுறா எண். இதை 1.4142135... என்ற முடிவுறாச் சுழல் தன்மையற்ற தசம எண்ணால் குறிப்பிடலாம்.)

3√3 (இது 31/3 −க்குச் சமமானது) ஒரு முறுடு. ஏனெனில், இது x3 − 3 = 0 என்ற சமன்பாட்டின் விகிதமுறா மூலம் ஆகும் ( √3 ஒரு விகிதமுறா எண், இதை 1.7320508... என்ற முடிவுறாச் சுழல் தன்மையற்ற தசம எண்ணால் குறிப்பிடலாம்). 

x2 − 6x + 7 = 0 போன்ற இருபடிச் சமன்பாடுகளைத் தீர்ப்பது பற்றி நீங்கள் அடுத்த வகுப்பில் கற்க இருக்கிறீர்கள். மேற்கண்ட சமன்பாடானது விகிதமுறு எண்களைக் கெழுக்களாகக் கொண்ட இருபடிச் சமன்பாடு, அதன் ஒரு மூலம் 3+√2 ஆனது ஒரு முறுடு ஆகும்.

√[1/25] ஒரு முறுடா? இல்லை; இதை 1/5 என்ற விகிதமுறு எண்ணாகச் சுருக்கி எழுத முடியும்.

4√[16/81] இன் மதிப்பு எவ்வாறு இருக்கும்? இது முறுடு அல்ல. இதனை 2/3 எனச் சுருக்க இயலும்.

நமக்குத் தெரிந்த மிக முக்கியமான விகிதமுறா எண் π ஒரு முறுடல்ல! அது ஒரு விகிதமுறா எண்ணாக இருந்த போதிலும், அதை √ குறியீட்டுக்குள் ஒரு விகிதமுறு எண்ணாக எழுத இயலாது. (அதாவது, விகிதமுறு கெழுக்களைக் கொண்ட எந்தவொரு சமன்பாட்டிற்கும் இது மூலமாக இருக்காது).

முறுடுகள் ஏன் முக்கியமாகின்றன? கணக்கீடுகள் செய்யும்போது, நாம் √2 = 1.414, மற்றும் √3 = 1.732 போன்ற தோராய மதிப்புகளை எடுத்துக்கொள்கிறோம்.

  (√2)2 = (1.414)2 = 1.99936 ≠ 2; 

  (√3)2 = (1.732)2 = 3.999824 ≠ 4 

இதிலிருந்து √2 மற்றும் √3 என்பவற்றின் தோராய மதிப்புகளை விட, வேறொரு துல்லியமான மற்றும் மிகச் சரியான மதிப்புகளை அவை கொண்டிருக்கின்றன என்பதை நம்மால் காண முடிகிறது. பொறியாளர்களும் விஞ்ஞானிகளும் பாலம் கட்டுதல், கட்டடக்கலை வேலைகள் போன்ற தங்கள் பணிகளைச் செய்யும்போது, மிகத் துல்லியமான மதிப்புகள் அவர்களுக்குத் தேவைப்படுகின்றன. எனவே முறுடுகளைப் பற்றி நாம் கற்பது இன்றியமையாததாகிறது.

முன்னேற்றத்தைச் சோதித்தல்

1. பொருத்தமில்லாதது எது? உமது விடைக்குத் தகுந்த காரணம் கூறவும்..

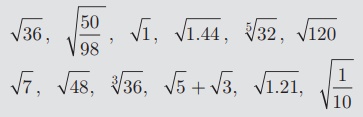
2. அனைத்து முறுடுகளும் விகிதமுறா எண்களா? உமது விடையைக் கலந்தாலோசிக்கவும்.

3. எல்லா விகிதமுறா எண்களும் முறுடுகளா? சில எடுத்துக்காட்டுகளைக் கொண்டு சரிபார்க்க.

1. முறுடின் வரிசை (Order of a surd)

ஒரு முறுடானது எந்த மூலத்திலிருந்து பெறப்படுகிறதோ, அந்த மூலத்தின் வரிசை அந்த முறுடின் வரிசை எனப்படுகிறது. n√a என்ற முறுடின் வரிசை n ஆகும். 5√99 இன் வரிசை என்ன? இது 5 ஆகும்.

முறுடுகளை பல்வேறு வழிகளில் வகைப்படுத்தலாம். 

(i) ஒரே வரிசை கொண்ட முறுடுகள் (Surds of Same order) இரண்டு அல்லது அதற்கு மேற்பட்ட முறுடுகளின் வரிசைகள் சமம் எனில் அந்த முறுடுகள் ஒரே வரிசை கொண்ட முறுடுகள் எனப்படும். இவை சம மூலக்குறியீடு கொண்ட முறுடுகள் எனவும் அழைக்கப்படும். எடுத்துக்காட்டாக,

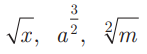என்பன இரண்டாம் வரிசை முறுடுகள் அல்லது இருபடி முறுடுகள்.

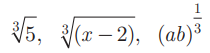என்பன மூன்றாம் வரிசை முறுடுகள் அல்லது கன முறுடுகள்.

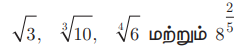என்பன வெவ்வேறு வரிசை கொண்ட முறுடுகள்.

(ii) முறுடின் எளிய வடிவம் (A surd in the simplest form) ஒரு முறுடின் எளிய வடிவம் என்பது அதை விகிதமுறு மற்றும் விகிதமுறா காரணிகளின் பெருக்கலாக எழுதும்போது, அதில் உள்ள விகிதமுறாக் காரணி கீழ்க்காணும் 3 விதிகளை நிறைவு செய்ய வேண்டும்.

(அ) மூலத்தின் வரிசை இயன்ற அளவு மிகச் சிறியதாய் இருக்க வேண்டும். 

(ஆ) மூலக் குறியீட்டின் வரிசை பின்னமாக இருத்தல் கூடாது. 

(இ) வரிசை n கொண்ட மூலக் குறியீடுக்குள் an வடிவில் எந்த ஒரு காரணியும் இருக்கக்கூடாது. இங்கு a ஒரு மிகை முழு.

எடுத்துக்காட்டு 2.18)

பின்வருவனவற்றை ஒரே வரிசை கொண்ட முறுடுகளாக மாற்ற இயலுமா? 

(i) √3 (ii) 4√3 (iii) 3√3

தீர்வு

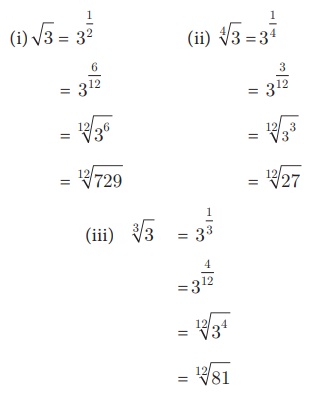
கடைசி வரியிலிருந்து, மூன்றையும் ஒரே வரிசை கொண்ட முறுடுகளாக மாற்ற முடிகிறது.

எடுத்துக்காட்டு 2.19

1. கொடுக்கப்பட்டுள்ள முறுடுகளை எளிய வடிவில் எழுதுக: i) √8 ii) 3√192

2. 3√7  > 4√5 என்பதை மெய்ப்பிக்க. 

தீர்வு

1. (i) √8 = √[4×2] = 2√2

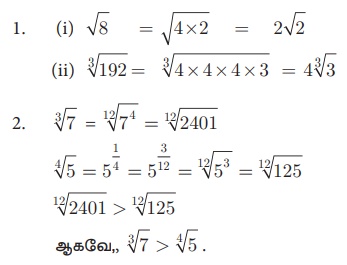
(iii) முழுமையான மற்றும் கலப்பு முறுடுகள் (Pure and Mixed Surds) எளிய வடிவில் ஒரு முறுடின் கெழு அல்லது குணகம் 1 எனில், அந்த முறுடு முழுமையான முறுடு எனப்படுகிறது.

எடுத்துக்காட்டாக, √3, 3√6, 4√7, 5√49 ஆகியவை முழுமையான முறுடுகள். ஒரு முறுடின் எளிய வடிவில் அதன் கெழு அல்லது குணகம் 1−ஐத் தவிர வேறு ஓர் எண்ணாக இருப்பின் அது கலப்பு முறுடு எனப்படுகிறது.

எடுத்துக்காட்டாக, 5√3, 2 4√5, 3 4√6 என்பன கலப்பு முறுடுகள். 

(iv) எளிய மற்றும் கூட்டு முறுடுகள் (Simple and Compound Surds) ஒரே ஓர் உறுப்பை மட்டும் கொண்டுள்ள முறுடு எளிய முறுடு எனப்படுகிறது. எடுத்துக்காட்டாக, √3, 2 √5 ஆகியன எளிய முறுடுகள். இரண்டு அல்லது அதற்கு மேற்பட்ட முறுடுகள் கூட்டுச் செயலிகளால் (+ அல்லது −) இணைக்கப்பட்டிருந்தால் அது கூட்டு முறுடு ஆகும். 

எடுத்துக்காட்டாக, √5 + 3√2 , √3 − 2√7, √5 − 7√2 + 6√3 ஆகியன கூட்டு முறுடுகள்.

(v) ஈருறுப்பு முறுடு (Binomial Surd) கூட்டல் அல்லது கழித்தல் முறையில் இணைத்து எழுதப்பட்ட விரிவில் இரண்டும் முறுடாகவோ அல்லது ஒன்று விகிதமுறு எண் மற்றொன்று ஒரு முறுடாகவோ இருப்பின் அது ஈருறுப்பு முறுடு எனப்படும். 

எடுத்துக்காட்டாக, ½ −√19, 5 + 3√2 , √3 − 2√7 ஆகியன ஈருறுப்பு முறுடுகள் ஆகும் .

எடுத்துக்காட்டு 2.20

ஏறுவரிசையில் எழுதுக: 3√2, 2√4, 4√3 

தீர்வு

 3√2, 2√4, 4√3 ஆகியவற்றின் வரிசைகள் 3, 2, 4. 

3, 2, 4 இன் மீ.பொ.ம = 12.

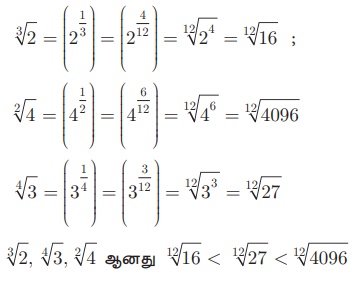
ஏறுவரிசை 3√2, 4√3, 2√4.

2. மூலக்குறியீட்டு விதிகள் (Laws of Radicals)

 m, n, என்பன மிகை முழுக்கள், a மற்றும் b என்பன மிகை விகிதமுறு எண்கள் எனில், கீழ்க்காணும் மூலக்குறியீட்டு விதிகளை நினைவு கூர்தல் பயனுள்ளது. 

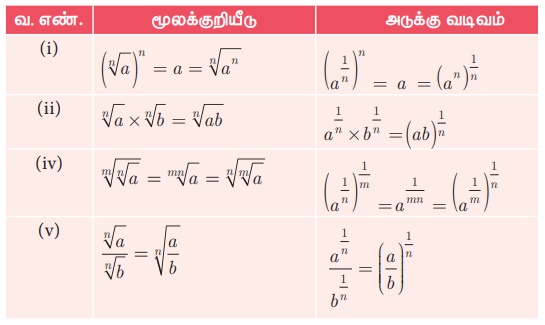
மூலக்குறியீட்டு விதிகளைப் பயன்படுத்தித் தீர்க்கக்கூடிய சில கணக்குகளைத் தற்போது விவாதிப்போம்.

எடுத்துக்காட்டு 2.21

கொடுக்கப்பட்ட முறுடுகளை அதன் எளிய வடிவில் எழுதுக. மேலும், அவற்றின் வரிசை, மூல அடிமானம் மற்றும் கெழு ஆகியவற்றையும் கண்டறிக.

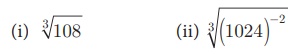
தீர்வு

வரிசை= 3; மூல அடிமானம்= 1/4 ; கெழு= 1/64

(அடுக்கு வடிவத்தைப் பயன்படுத்தியும் இதே முடிவுகளைப் பெற இயலும்).

குறிப்பு

 5 மற்றும் 6 என்ற எண்களைக் கருதுக. மேலும் 5 = √25 மற்றும் 6 = √36 ஆகும். 

ஆகவே, √26, √27, √28, √29, √30, √31, √32, √33, √34, மற்றும் √35 என்பன 5 −க்கும் 6 −க்கும் இடைப்பட்ட முறுடுகளாகும்.

3√2 = √[32 × 2] = √18, 2√3 = √[22 ×3] = √12 ஆகவே, √17, √15, √14, √13 என்பன 2√3 −க்கும் 3√2 −க்கும் இடைப்பட்ட முறுடுகளாகும்.

3. முறுடுகளில் நான்கு அடிப்படைச் செயல்கள் (Four Basic Operations on Surds)

(i) முறுடுகளில் கூட்டல் மற்றும் கழித்தல் (Addition and subtraction of surds) ஒத்த முறுடுகளைக் கீழ்க்காணும் விதியைப் பயன்படுத்திக் கூட்டவோ கழிக்கவோ முடியும்.

   a n√b  ±  c n√b = (a ± c) n√b, இங்கு b > 0.

எடுத்துக்காட்டு 2.22

(i) 3√7 மற்றும் 5√7 ஐக் கூட்டுக. அவற்றின் கூடுதல் ஒரு விகிதமுறு எண்ணா அல்லது விகிதமுறா எண்ணா எனச் சரிபார்க்க.

(ii) 4√5 ஐ7√5 இலிருந்து கழிக்க. தீர்வானது ஒரு விகிதமுறு எண்ணா அல்லது விகிதமுறா எண்ணா ? 

தீர்வு

(i) 3√7 + 5√7 = (3 + 5) √7 = 8√7. தீர்வு ஒரு விகிதமுறா எண். 

(ii) 7√5 − 4√5 = (7 − 4) √5 = 3√5 . தீர்வு ஒரு விகிதமுறா எண்.

எடுத்துக்காட்டு 2.23 

கீழ்க்காண்பவற்றைச் சுருக்குக:

(i) √63 − √175 + √28 

(i) 2 3√40 + 3 3√625 – 4 3√320

தீர்வு

(i) √63 − √175 + √28 = √[9×7] − √[25×7] + √[4×7]

= 3√7 − 5√7 + 2√7

 = (3√7 +2√7) − 5√7 

= 5√7 − 5√7

= 0

(ii) 2 3√40  +  3 3√625  –  4 3√320

= 2 3√[8×5]  +  3 3√[125×5]  –  4 3√[64 × 5]

 = 2 3√[23×5]  +  3 3√[53×5]  –  4 3√[43×5] 

= ( 2 × 2 3√5 )  +  ( 3 × 5 3√5 )  –  ( 4 × 4 3√5 )

= 4 3√5  +  15 3√5  –  16 3√5 

= (4+ 15 − 16) 3√5 = 3 3√5

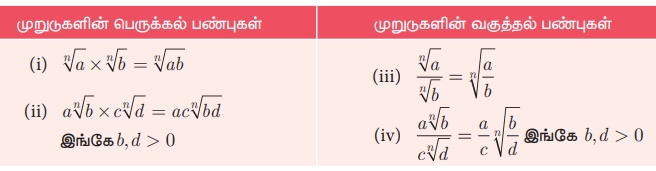
(ii) முறுடுகளில் பெருக்கல் மற்றும் வகுத்தல் (Multiplication and division of surds)

ஒத்த முறுடுகளைக் கீழ்க்காணும் விதிகளைப் பயன்படுத்திப் பெருக்கவோ அல்லது வகுக்கவோ முடியும். 

எடுத்துக்காட்டு 2.24

 3√40 மற்றும் 3√16 ஐப் பெருக்குக. 

தீர்வு 

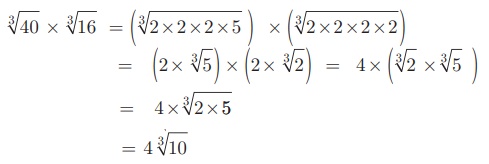
எடுத்துக்காட்டு 2.25

 2√72 × 5√32 × 3√50 இன் மதிப்பைக் கணக்கிட்டு விடையை எளிய வடிவில் தருக. 

தீர்வு

2√72 = √[36×2] = 6√2

√32 = √[16×2]= 4√2

√50 = √[25×2] = 5√2

2√72 × 5√32 × 3√50 = ( 2 × 6√2) × (5 × 4√2) × (3 × 5√2)

= 2×5×3×6×4×5×√2×√2×√2 

= 3600×2√2

= 7200√2

எடுத்துக்காட்டு 2.26

9√8 என்ற முறுடை 6√6 ஆல் வகுக்க. 

தீர்வு

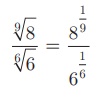(6, 9 இன் மீ.பொ.ம 18 என்பதைக் குறித்துக் கொள்க.)

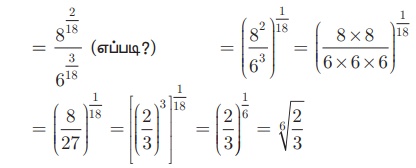
செயல்பாடு − 1

கீழ்க்காணும் முடிவுகள் ஆர்வமானதாக இருக்கிறதா?

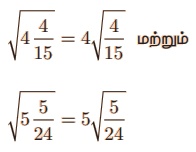
என்பவை சரியா என ஆராய்க. இதே வடிவில் மேலும் 4 புதிய முறுடுகளைக் காண்க.

செயல்பாடு−2

வரைபடத்தாளை எடுத்து, அதில் O, A, B, C ஐப் பின்வருமாறு குறிக்க.

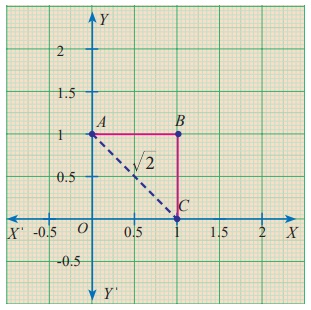
சதுரம் OABC இல்,

OA = AB = BC = OC = 1 அலகு 

செங்கோண ΔOAC இல், 

AC = √[12 +12 ]

= √2 அலகு (பிதாகரஸ் தேற்றப்படி)

மூலைவிட்டத்தின் நீளம் AC = √2 , ஒரு முறுடாகும்.

கீழ்க்காணும் வரைபடங்களைக் கருதுக.

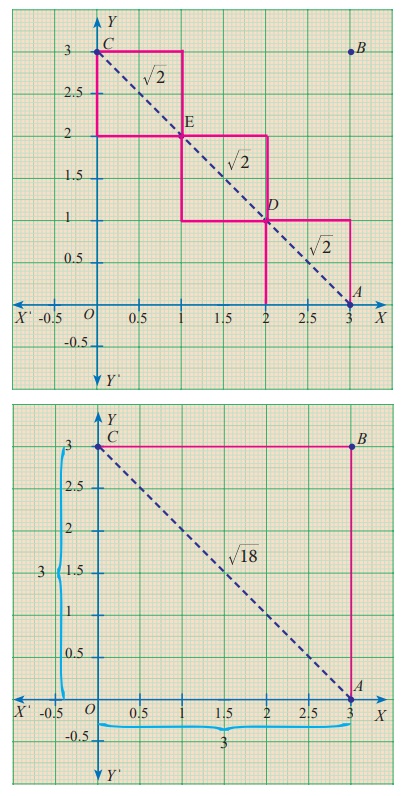
மூலைவிட்டம் AC இன் நீளத்தை இரு வேறு வழிகளில் காணலாம்.

AC = AD + DE + EC

 (ஓரலகு சதுரங்களின் மூலைவிட்டம்)

AC = √2 + √2 + √2 = 3√2 அலகுகள்  ……. (1)

AC = √ [ OA2 + OC2] = √ [32 + 32] 

AC = √ [ 9 + 9 ] = √18 அலகுகள்       ……. (2)

இவை சமமா? விவாதிக்க. 

இதே செயலை வேறுபட்ட பக்க அளவுகளைக் கொண்ட சதுரங்களை எடுத்துச் சரிபார்க்க.