வரையறை, தேற்றம், நிரூபணம் - வெக்டர் முப்பெருக்கல் (Vector triple product) | 12th Maths : UNIT 6 : Applications of Vector Algebra
12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்
வெக்டர் முப்பெருக்கல் (Vector triple product)
வெக்டர் முப்பெருக்கல் (Vector triple product)
வரையறை 6.5
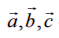 என்பன தேனும் மூன்று வெக்டர்கள் எனில்,
என்பன தேனும் மூன்று வெக்டர்கள் எனில், 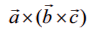 என்பது இம் மூன்று வெக்டர்களின் வெக்டர் முப்பெருக்கல் என அழைக்கப்படுகிறது.
என்பது இம் மூன்று வெக்டர்களின் வெக்டர் முப்பெருக்கல் என அழைக்கப்படுகிறது.
குறிப்பு
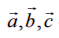 என்பன ஏதேனும் மூன்று வெக்டர்கள் எனில்,
என்பன ஏதேனும் மூன்று வெக்டர்கள் எனில், 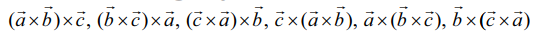 என்பனவும் வெக்டர் முப்பெருக்கல்கள் ஆகும்.
என்பனவும் வெக்டர் முப்பெருக்கல்கள் ஆகும்.
வெக்டர் பெருக்கலில் நன்கறியப்பட்ட பண்புகளின் விளைவாக பின்வரும் தேற்றத்தைப் பெறுகிறோம்.
தேற்றம் 6.7
வெக்டர் முப்பெருக்கல் பின்வரும் பண்புகளை நிறைவு செய்கிறது.
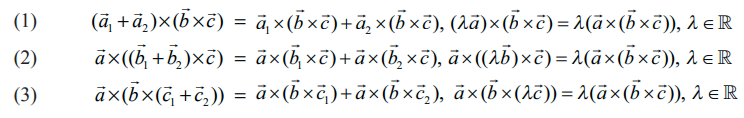
குறிப்புரை
வெக்டர் பெருக்கல் சேர்ப்புப் பண்பை நிறைவு செய்யாது. அதாவது 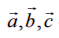 என்ற வெக்டர்களுக்கு
என்ற வெக்டர்களுக்கு 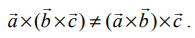
நியாயப்படுத்துதல்
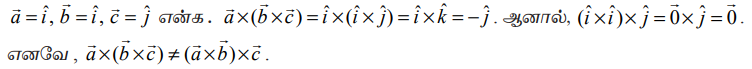
வெக்டர் முப்பெருக்கலை, திசையிலிப் பெருக்கல் வாயிலாக விளக்க ஒரு எளிய சூத்திரத்தைப் பின்வரும் தேற்றம் வழங்குகிறது.
தேற்றம் 6.8 (வெக்டர் முப்பெருக்கல் விரிவாக்கம்) (Vector Triple product expansion)
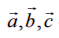 என்பன ஏதேனும் மூன்று வெக்டர்கள் எனில்,
என்பன ஏதேனும் மூன்று வெக்டர்கள் எனில், 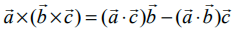 ஆகும்.
ஆகும்.
நிரூபணம்
ஆய அச்சுக்களைப் பின்வருமாறு தேர்வு செய்வோம்:
![]() செயல்படும் நேர்க்கோட்டுத் திசையில் x−அச்சையும்,
செயல்படும் நேர்க்கோட்டுத் திசையில் x−அச்சையும், ![]() வழியாகசெல்வதும்
வழியாகசெல்வதும் ![]() வெக்டருக்கு இணையானதுமான தளத்தில் உள்ளவாறு y−அச்சையும், மற்றும்
வெக்டருக்கு இணையானதுமான தளத்தில் உள்ளவாறு y−அச்சையும், மற்றும் ![]() ,
, ![]() ஆகியவற்றை உள்ளடக்கிய தளத்திற்கு செங்குத்தாக z−அச்சையும் தேர்வு செய்க.
ஆகியவற்றை உள்ளடக்கிய தளத்திற்கு செங்குத்தாக z−அச்சையும் தேர்வு செய்க.
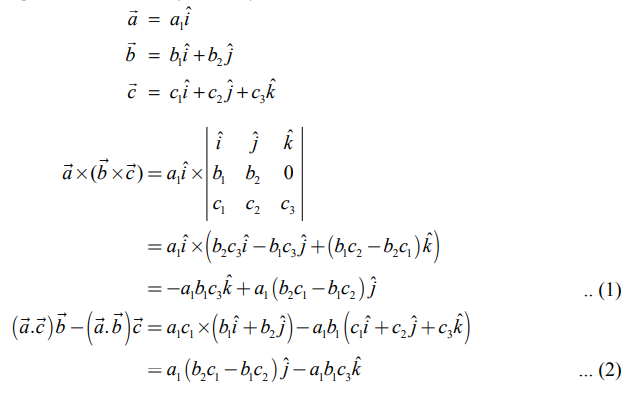
சமன்பாடுகள் (1) மற்றும் (2) ஆகியவற்றில் இருந்து
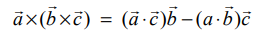 எனக் கிடைக்கிறது.
எனக் கிடைக்கிறது.
குறிப்பு
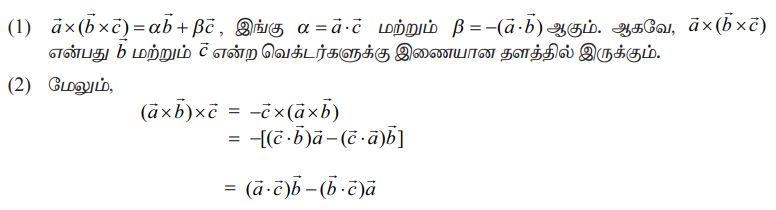
எனவே, 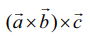 என்பது
என்பது ![]() மற்றும்
மற்றும் ![]() என்ற வெக்டர்களுக்கு இணையாக உள்ள தளத்தில் இருக்கும்.
என்ற வெக்டர்களுக்கு இணையாக உள்ள தளத்தில் இருக்கும்.
(3) 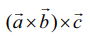 என்ற வெக்டரில், அடைப்புக் குறிக்குள் உள்ள
என்ற வெக்டரில், அடைப்புக் குறிக்குள் உள்ள ![]() என்ற வெக்டரை நடுவில் உள்ள வெக்டர் எனவும்,
என்ற வெக்டரை நடுவில் உள்ள வெக்டர் எனவும், ![]() என்ற வெக்டரை நடுவில் இல்லாத வெக்டர் எனவும் கருதுக. இதேபோல்,
என்ற வெக்டரை நடுவில் இல்லாத வெக்டர் எனவும் கருதுக. இதேபோல், 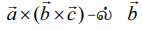 என்று வெக்டரை நடுவில் உள்ள வெக்டராகவும்
என்று வெக்டரை நடுவில் உள்ள வெக்டராகவும் ![]() என்ற வெக்டரை நடுவில் இல்லாத வெக்டராகவும் கருதுக. இப்பொழுது, இவ்வெக்டர்களின் வெக்டர் முப்பெருக்கல்
என்ற வெக்டரை நடுவில் இல்லாத வெக்டராகவும் கருதுக. இப்பொழுது, இவ்வெக்டர்களின் வெக்டர் முப்பெருக்கல்
λ (நடுவில் உள்ள வெக்டர்) − μ (நடுவில் இல்லாத வெக்டர்)
என்றமைவதைக் காணலாம். இங்கு λ என்பது நடுவில் இல்லாத வெக்டர்களின் புள்ளிப் பெருக்கலாகும் மற்றும் μ என்பது நடுவில் இல்லாத வெக்டரைத் தவிர மற்ற வெக்டர்களின் புள்ளிப் பெருக்கலாகும் என்பதை அறிக.