அடிப்படை முடிவுகளின் மீள்பார்வை

அடிப்படை முடிவுகளின் மீள்பார்வை (A recall of Basic Results)

முந்தைய வகுப்புகளில் செங்கோண முக்கோணத்தைப் பயன்படுத்தி முக்கோணவியலின் விகிதங்களையும் மற்றும் குறுங்கோண முக்கோணவியலின் முற்றொருமைகளையும் படித்தோம். இரு கோள்களுக்கு இடைப்பட்ட தொலைவு, மலையின் உயரம், சந்திரன் மற்றும் சூரியன் போன்ற மிகத் தொலைவில் உள்ளவைகளின் தூரம், மிகப் பிரம்மாண்டமான கட்டிடங்களின் உயரம், அதிவேக விமானங்களின் திசைவேகம் ஆகியவற்றைக் கணக்கிடுவது விந்தையாக உள்ளது. அதுபோன்ற  உயரங்கள் மற்றும் தூரங்களைக் குறுங்கோண முக்கோணவியலின் விகிதங்களைக் கொண்டு கணக்கிடுவது ஆர்வ மிகுதியைக் காட்டுகிறது. ஏதேனும் ஒரு மெய்யெண்ணிற்கு முக்கோணவியல் சார்பை வரையறுத்து அதனை கணிதத்தின் அனைத்துப் பாடப்பிரிவுகளிலும் பயன்படுத்துவது குறிப்பாக நுண்கணிதத்தில் பயன்படுத்துவது நமது குறிக்கோளாகும். முதலாவதாகக் கோணம் மற்றும் கோணத்தின் பாகை அளவின் வரையறைகளை நினைவு கூறுவோம்.

1. கோணங்கள் (Angles)

OA, OB ஆகிய இரண்டு கதிர்கள் O என்ற பொதுவான புள்ளியைக் கொண்டு படம் 3.1-ல் காட்டியவாறு கோணம் ∠AOB-ஐ உருவாக்கும். பொதுவான புள்ளி O - வை உச்சி என்றும், இரண்டு கதிர்கள் கோணத்தின் பக்கங்கள் என்றும் அழைக்கப்படுகிறது.

கோணத்தின் ஆரம்பப் பக்கம் OA என அழைக்கப்படுகிறது. ஆரம்ப A கோணம் நிலை OA-விலிருந்து OB வரை ஒரு கதிரை சுழற்றிய பின் OB ஆனது கோணத்தின் முனையப் பக்கம் என்று அழைக்கப்படுகிறது.

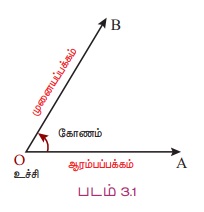
இடஞ்சுழி சுழற்சி ஒரு நேர்மறை கோணத்தை உருவாக்குகிறது. (நேர்மறை அடையாளம் கோணத்தில்), ஒரு வலஞ்சுழி சுழற்சி ஒரு எதிர்மறை கோணத்தை உருவாக்குகிறது. (எதிர்மறை அடையாளம் கோணத்தில்)

குறிப்பு: இடஞ்சுழியாக (வலஞ்சுழியாக) OA-ஐ அதன் மீது ஒன்றிணையும்படி முழுமையாகச் சுற்றப்படுவதை ஒரு முழு வட்டச் சுற்று அல்லது சுழற்சி என்கிறோம்.

2. கோண அளவீடுகளின் பல்வேறு அமைப்புகள் (Different Systems of measurement of angle) 

கோணங்களை அளவிடுவதற்கு மூன்று வகையான அமைப்புகள் உள்ளன. அவையாவன,

(i) அறுபான் அமைப்பு (Sexagesimal system)

அறுபான் அமைப்பின் கோண அளவீட்டு முறை பெரிதும் பயன்படுத்தப்படுகிறது. இதில் செங்கோணத்தை 90 சம பாகங்களாகப் பிரித்து அதைப் பாகை (Degree) என்றும், ஒரு பாகையை 60 சம பாகங்களாகப் பிரித்து அதனைக் கலைகள் (Minutes) என்றும், ஒரு கலையை 60 சம பாகங்களாகப் பிரித்து அதனை விகலைகள் (Seconds) என்றும் அழைக்கிறோம். ஒரு பாகை, ஒரு கலை மற்றும் ஒரு விகலை ஆகியவை முறையே 1°, 1', 1" எனக் குறிக்கப்படுகிறது.

(ii) நூற்றின் கூறு அமைப்பு (Centesimal system)

நூற்றின் கூறு அமைப்பில் ஒரு செங்கோணத்தை 100 சம்பாகங்களாகப் பிரித்து அதனைத் தரம் (Grades) என்றும், ஒரு தரத்தை 100 சம பாகங்களாகப் பிரித்து அதனைக் கலைகள் (Minutes) என்றும், ஒரு கலையை 100 சமபாகங்களாகப் பிரித்து அதனை விகலைகள் (Seconds) என்றும் அழைக்கிறோம். இதனை 1g என்ற குறியீடு ஒரு தரத்தைக் குறிக்கிறது.

(iii) வட்டமுறை அமைப்பு (Circular system) 

வட்டமுறை அமைப்பில் ஆரையன் (Radian) அளவீடு அவ்வட்டத்தின் வில்லின் நீளம் மற்றும் அதன் ஆரத்தைக் கொண்டு வரையறுக்கப்படுகிறது. வட்டமுறை அமைப்பு கணிதத்தின் அனைத்து பிரிவுகளிலும் மற்றும் அறிவியலிலும் பெரிதும் பயன்படுகின்றன. 1c என்ற குறியீடு ஓர் ஆரையன் அளவை குறிக்கிறது.

3. பாகை அளவு (Degree Measure)

கோணங்களின் அளவீட்டு அலகை ஒரு பாகை என்றும் அதனைக் குறியீட்டின் மூலம் ° என்றும் குறிக்கலாம். நாம் ஒரு முழுவட்டச் சுற்றை 360 சம பாகங்களாகப் பிரித்து ஒவ்வொரு பகுதியையும் ஒரு பாகை என்கிறோம். ஒரு பாகை 1° என்பது ஒரு முழுச் சுழற்சியில் 1/360 ஆகும். கோணத்தின் ஒரு பகுதியை அளவிட மற்றும் கோணங்களின் அளவீடுகளின் துல்லியத்திற்காக, கலைகள் மற்றும் விகலைகள் அறிமுகப்படுத்தப்படுகின்றன. ஒரு கலை (1') என்பது ஒரு பாகையில் (1/60) ஆகும், ஒரு விகலை (1") என்பது ஒரு கலையில் (1/60) ஆகும் அல்லது ஒரு பாகையில் (1/3600) ஆகும்.

சிறப்பாகப் புரிந்து கொள்வதற்கும் மற்றும் பயன்பாட்டிற்கும் பின்வரும் வகையில் சோடி கோணங்களை நாம் வகைப்படுத்தலாம்.

(i) ஒரே அளவை கொண்ட இரு கோணங்கள் ஒத்த கோணங்க என்று அழைக்கப்படுகின்றன. 

(ii) இரண்டு கோணங்களின் கூடுதல் 90° எனில், அவை நிரப்புக்கோணங்கள் என்று அழைக்கப்படுகின்றன.

(iii) இரண்டு கோணங்களின் கூடுதல் 180° எனில் அவைமிகை நிரப்புக்கோணங்கள் என்று அழைக்கப்படுகின்றன. 

(iv) 0°-விற்கும் 360°-விற்கும் இடைப்பட்ட இரண்டு கோணங்களின் கூடுதல் 360° எனில், அவை இணையிய கோணங்கள் என்று அழைக்கப்படுகின்றன.

குறிப்பு: (i) நாம் எங்கெல்லாம் ஒரு பாகையை ஒரு மணி நேரம் குறிக்கும் என்று நினைக்கிறோமோ அங்கெல்லாம் பாகை, கலை மற்றும் விகலை என்ற கருத்து, நேர அளவீட்டு முறைக்குச் சமமானதாகும்.

(ii) கவனிக்க

4. திட்ட நிலையில் உள்ளகோணங்கள் (Angles in Standard Position)

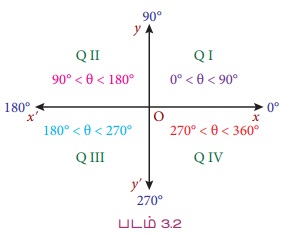
ஒரு கோணத்தின் உச்சியானது O-விலும், அதன் ஆரம்பப் பக்கம் மிகை x-அச்சாகவும் செயல்பட்டால் கோணம் திட்ட நிலையில் இருப்பதாகக் கூறலாம்.

திட்ட நிலையில், கோணத்தின் முனையப் பக்கம் முதல் காற்பகுதியில் விழுந்தால் கோணம் முதல் காற்பகுதியில் இருக்கும் என்று கூறலாம். இதே போன்று நாம் மற்ற மூன்று காற்பகுதிகளை வரையறுக்கலாம்.

திட்ட நிலையில், கோணங்களுக்கான முனையப் பக்கம் x-அச்சு அல்லது y-அச்சு வழியாக அமைந்தால் அக்கோணங்களைக் காற்பகுதி கோணங்கள் (Quadrantal Angles) என்று அழைக்கலாம். எனவே, 0°; 90°; 180°; 270° மற்றும் 360° ஆகியவை காற்பகுதி கோணங்கள் ஆகும்.

குறிப்பு: காற்பகுதி கோணத்தின் பாகை அளவீடு 90°-ன் மடங்காகும்.

5. இணை முனையக் கோணங்கள் (Coterminal angles)

நாம் கதிரை இடஞ்சுழியாக முழுமையாகச் சுழற்றினால் அளவிடும் கோணம் 360° ஆகும். இடஞ்சுழியாக தொடர்ந்து சுழற்றிக் கொண்டிருந்தால் அளவிடும் கோணம் 360°-ஐ மிகும். வலஞ்சுழியாக சுழற்றினால் குறை கோணத்தை (Negative Angle) ஏற்படுத்தும்.

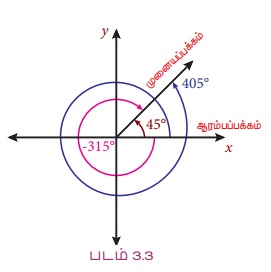
கோணங்கள் 57°, 417° மற்றும் -303° ஆகிய கோணங்கள் ஒரே ஆரம்ப மற்றும் முனையப் பக்கங்களை கொண்டவை, ஆனால் வெவ்வேறு அளவுகளாலான சுழற்சிகளைக் கொண்டவை இது போன்ற கோணங்களை இணைமுனையக் கோணங்கள் (coterminal angles) என்று அழைக்கலாம். அதாவது ஒரே முனையம் கொண்ட திட்ட நிலையில் உள்ள கோணங்களை இணை முனையக் கோணங்கள் (coterminal angles) என்று அழைக்கலாம்.

α மற்றும் β ஆகியவை இணை முனையக் கோணங்கள் எனில் β = α + k (360°), இங்கு k என்பது ஒரு முழு எண். திட்ட நிலையில் ஒரே முனையம் கொண்ட கோணங்களின் அளவீட்டு வித்தியாசம் 360° ன் முழு எண் மடங்கில் இருக்கும்.

எடுத்துக்காட்டாக, 417° மற்றும் -303° ஆகியவை இணை முனையக் கோணங்கள். ஏனெனில்

417° - (- 303°) = 720° = 2 (360°).

குறிப்பு: (i) 45°, - 315° மற்றும் 405° ஆகியவை முதல் காற்பகுதியில் அமையும் என்பதை கவனியுங்கள்.... 

(ii) (30°, 390°), (280°, 1000°) மற்றும் (-85°, 275°) ஆகிய கோணங்களின் சோடிகள் இணை முனையக் கோணங்கள் ஆகும்.

6. செங்கோண முக்கோணத்தைப் பயன்படுத்தி அடிப்படை முக்கோணவியல் விகிதங்கள் (Basic Trigonometric ratios using a right triangle)

செங்கோண முக்கோணம் ABC இல் a, b, c ஆகிய பக்கங்களின் நீளங்கள் ஆறு விகிதங்களை உருவாக்கும் என்பதை நாம் நன்கறிவோம். அவ்விகிதங்கள் முக்கோணவியலில் ஆறு அடிப்படை சார்புகளை வரையறுக்க வழிவகுக்கும்.

முதலாவதாக, ஒரு செங்கோண முக்கோணத்தை குறிப்பாக வைத்து வரையறுக்கப்பட்ட முக்கோணவியல் விகிதங்களை நாம் நினைவு கூறுவோம்.

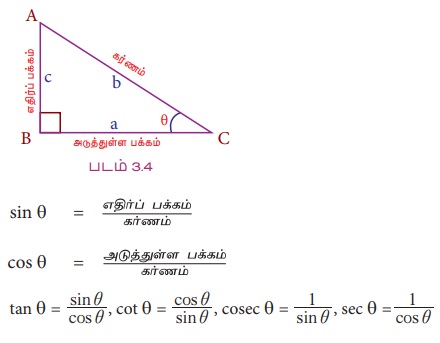
ஆகியவற்றை முக்கோணவியல் விகிதங்கள் sin θ மற்றும் cos θ - வை பயன்படுத்திக் காணலாம்.

7. பரவலாக பயன்படுத்தப்படும் கோணங்களின் முக்கோணவியல் சார்புகளின் சரியானமதிப்புகள் (Exact Values for trigonometric functions of widely used angles) 

அறிந்த கோணங்களின் முக்கோணவியல் சார்புகளின் மதிப்புகளை பட்டியலிடுவோம்.

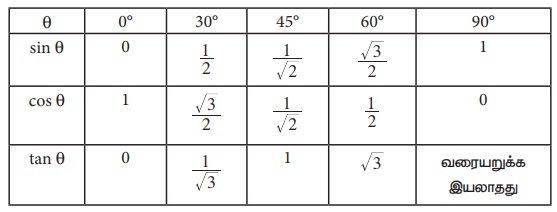
குறிப்பு: (i) மேலே கொடுக்கப்பட்ட அனைத்து மதிப்புகளும் மிகச் சரியானவையாகும்.

(ii) sin 30° மற்றும் cos 60° இன் மதிப்புகளும் sin 60° மற்றும் cos 30° ஆகியவற்றின் மதிப்புகளும் சமம் என்பதைக் கவனத்தில் கொள்க. 

(iii) தலைகீழ் விகித மதிப்புகளான cosecant, secant மற்றும் cotangent ஆகியவைகளை மேற்கண்ட அட்டவணையின் மூலம் பெறலாம்.

(iv) cos 90° = 0 என்பதால், tan 90° மற்றும் sec 90° ஆகியவை வரையறுக்க இயலாதவையாகிறது. 

(v) sin 0° = 0 என்பதால் cot 0° மற்றும் cosec 0° ஆகியவை வரையறுக்க இயலாதவையாகிறது.

8. அடிப்படை முக்கோணவியல் முற்றொருமைகள் (Basic Trigonometric Identities)

சார்பகத்தில் அனுமதிக்கப்பட்ட அனைத்து மதிப்புகளுக்கும் ஒரு முக்கோணவியல் முற்றொருமை எப்பொழுதும் உண்மை என்ற உறவைத் தெரிவிக்கிறது. எடுத்துக்காட்டாக, sec θ = 1/cos θ என்பது θ-ன் அனுமதிக்கப்பட்ட அனைத்து மதிப்புகளுக்கும் இந்த உறவு உண்மையாகிறது. எனவே, இது ஒரு முற்றொருமையாகும். மேலும், sin θ = 1/2  ஒரு முற்றொருமையல்ல. ஏனெனில் θ = 60° எனும் போது இந்த உறவு உண்மையற்றதாகும். சிக்கலான கோவைகளை எளிமைப்படுத்த முற்றொருமைகள் நமக்குப் பயன்படுகிறது. அவைகள் முக்கோணவியல் சமன்பாடுகளைத் தீர்ப்பதற்குப் பெரிதும் பயன்படுகிறது.

முற்றொருமைகளை கையாண்டு அதனைத் திருத்தி அமைப்பதற்கு இயற்கணிதத்தின் பல்வேறு யுக்திகள் உதவி புரிகின்றன.

முக்கோணவியலில் அடிப்படை முற்றொருமைகளை (பித்தாகோரியன் முற்றொருமைகள்) நினைவு கூறுவோம், குறிப்பாக

cos2 θ + sin2 θ = 1; sec2 θ - tan2 θ = 1; cosec2 θ – cot2 θ = 1

குறிப்பு: (i) sin2 θ என்பது (sin θ)2 - ஐக் குறிக்கும். இந்த முறை மற்ற முக்கோணவியல் விகிதங்களுக்கும் பொருந்தும். 

(ii) θ = 90° எனில் sec2θ – tan2θ = 1 என்பது அர்த்த மற்றதாகும். sec θ மற்றும் tan θ ஆகியவை வரையறுக்கப்படும் அனைத்து 0 - வின் மதிப்புகளுக்கும் உண்மை இருப்பினும் இது ஒரு முற்றொருமையாகும். ஆகவே, சார்பகத்தின் அனைத்து மதிப்புகளுக்கும் முற்றொருமை ஒரு சமன்பாடு என்பது உண்மையாகும்.

(iii) sin θ / 1 + cos θ என்ற கோவை, 1 + cos θ + θ - விற்கு, θ -ன் அனைத்து மதிப்புக்களுக்கும் செல்லுபடியாகும் என்பதை நாம் புரிந்துகொள்ள வேண்டும்.

எடுத்துகாட்டும் 3.1  நிறுவுக. tan θ + sec θ – 1 / tan θ – sec θ + 1 = 1+ sin θ / cos θ.

தீர்வு:

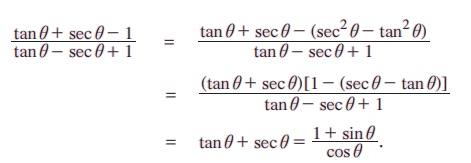
எடுத்துக்காட்டு 3.2

நிறுவுக: (sec A - cosec A) (1 + tan A + cot A) = tan A sec A - cot A cosec A. 

தீர்வு:

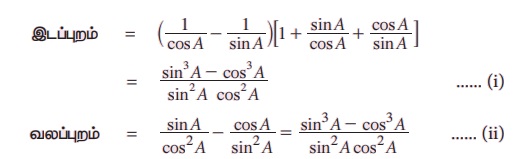
(i) மற்றும் (ii) இலிருந்து நமக்குத் தேவையான தீர்வு கிடைத்துள்ளது.

எடுத்துக்காட்டு 3.3 a cos θ = b மற்றும் c sin θ = d லிருந்து θ -ஐ நீக்குக, a, b, c, d ஆகியவை மாறிலிகள். 

தீர்வு:

ac cos θ = bc மற்றும் ac sin θ = ad ஆகியவற்றை வர்க்கப்படுத்திக் கூட்டக் கிடைப்பது

a2 c2 = b2 c2+ a2 d2

பயிற்சி 3.1

1. கொடுக்கப்பட்ட கோணங்கள் எந்தக் காற்பகுதியில் அமையும் என்பதைக் காண்க.

(i) 25°

(ii) 825° 

(iii) - 55° 

(iv) 328° 

(v) - 230° 

2. 0° ≤ θ < 360° - ல் கொடுக்கப்பட்ட ஒவ்வொரு கோணத்திற்கான இணைமுனையக்கோணத்தை காண்க.

(i) 395°

(ii) 525° 

(iii) 1150° 

(iv) - 270° 

(v) - 450° 

3. acos θ - bsin θ = c எனில், asin θ + bcos θ = 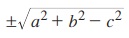என்பதை நிறுவுக.

4. sin θ + cos θ = m எனில், cos6 θ + sin6 θ = 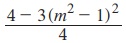என நிறுவுக.

(இங்கு m2 < 2).

5. 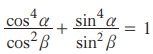எனில்,

(i) sin4 α + sin4 β = 2 sin2 α sin2 β 

(ii) 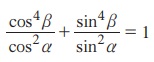என நிறுவுக.

6. என நிறுவுக.

7. 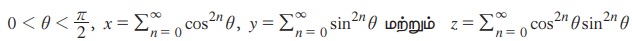எனில், xyz = x+y+ z என நிறுவுக.

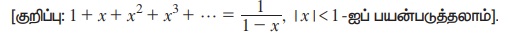
8. tan2θ = 1 – k2 எனில், secθ + tanθ cosecθ = (2 – k2)3/2 என நிறுவுக. மேலும் இவற்றை நிறைவு செய்யும் k இன் மதிப்பைக் காண்க.

9. secθ+ tanθ = p எனில், secθ, tanθ மற்றும் sinθ ஆகியவற்றின் மதிப்பை p இன் வாயிலாகக் காண்க.

10. cot θ (1 + sinθ) = 4m மற்றும் cotθ (1 – sinθ) = 4n எனில், (m2 – n2)2 = mn என நிறுவுக.

11. cosecθ – sinθ = a3 மற்றும் secθ – cosθ = b3 எனில், a2 b2(a2 + b2) = 1 என நிறுவுக.

12. a secθ – c tanθ = b மற்றும் b secθ + d tanθ = c ஆகிய சமன்பாடுகளிலிருந்து θ ஐ நீக்குக.