முக்கோணங்களின் முற்றொருமைகள்

முக்கோணங்களின் முற்றொருமைகள் (Trigonometric Identities)

1. கூட்டுக்கோணங்களின் சூத்திரங்கள் அல்லது கூட்டல் அல்லது கழித்தல் முற்றொருமைகள் (Sum and difference identities or compound angles formulas)

கூட்டுக்கோணங்கள் என்பது இரண்டு அல்லது அதற்கும் மேற்பட்ட கோணங்களின் கூடுதல் ஆகும். f (x + y) = f (x) + f (y) மற்றும் f (kx) = kf (x), ( k என்பது ஒரு மெய்யெண்) போன்ற சார்புகளின் தொடர்பை முக்கோணவியல் சார்புகள் பூர்த்தி செய்யாது. எடுத்துக்காட்டாக cos(α + β) + cos α + cos β, sin (2a) ≠ 2 sin α, tan 3 α + 3tan α ... இவ்வாறு sin(α + β), cos (α + β), .. போன்ற சூத்திரங்களைக் தருவிப்பது அவசியம் மற்றும் அதைப் பயன்பாட்டு கணக்குகளில் கணக்கிடுவதற்கு பயன்படுத்தப்படுகின்றன.

செவிப்பறையில் அழுத்தத்தை உருவாக்கும் அதிர்வுகளால் இசையானது உருவாகியுள்ளது. இசை ஒலி சைன் வளைக்கோட்டு வரைபடங்கள் மாதிரிகளாக இருக்கலாம் (y = sin x அல்லது y = cos x போன்ற வரைபடங்களைப் போன்றது), ஒன்றுக்கு மேற்பட்ட ஒலிகள் ஒலிக்கும்போது ஏற்படும் விளைவு அழுத்தமானது ஒவ்வொரு தனிப்பட்ட ஒலிகள் ஏற்படும் அழுத்தத்தின் கூடுதலுக்குச் சமமாகும். இச்சூழலில் முக்கோணவியலின் கூடுதல் மற்றும் கழித்தல் முற்றொருமைகள் முக்கியமாக பயன்படுத்தப்படுகின்றன. அத்துடன் அலைகளின் பகுப்பாய்வில் முக்கோணவியலின் கூடுதல் மற்றும் கழித்தல் முற்றொருமைகள் பயனுள்ளதாக இருக்கின்றன.

இரண்டு கோணங்களின் கூடுதலின் கொசைன் முற்றொருமையை முதலில் நாம் நிறுவுவோம், மற்றும் இதனை அனைத்து முக்கோணவியல் விகிதங்களுக்கும் நீட்டிப்போம். 

முற்றொருமை 3.1: cos (α + β) = cos α cos β - sin α sin β

நிரூபணம் :

O -ஐ மையமாகக் கொண்ட ஓரலகு வட்டத்தைக் கருத்தில் கொள்க. P = P (1, 0) என்க. ∠ POQ = a, ∠ POR = α + β மற்றும் ∠POS = - β என்றமையும்படி Q, R மற்றும் S புள்ளிகளை ஓரலகு வட்டத்தில் படம் 3.15 இல் காட்டியபடி குறிக்க. α, α + β மற்றும் – β ஆகியவை திட்டநிலையிலுள்ளன. இப்பொழுது Q, R மற்றும் S ஆகிய புள்ளிகள், Q(cos α, sin α), R(cos(α + β), sin(α + β)) மற்றும் S(cos(-β), sin(-β)) ஆகக் கொடுக்கப்படுகிறது. ∆ POR மற்றும் ∆ SOQ ஆகியவை சர்வசமமுடையதாகிறது. எனவே,

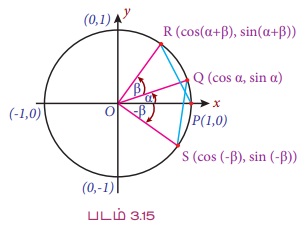
PR = SQ , ஆனது PR2 = SQ2-ஐக் கொடுக்கிறது.

ஆகவே,

[cos(α + β) - 1]2 + sin2 (α + β) = [cos α - cos(-β) ]2 + [sin α - sin(-β) ]2

- 2 cos(α+ β) + 2 = 2 - 2 cos α cos β+ 2 sin α sin β 

எனவே, cos (α + β) = cos α cos β - sin α sin β

குறிப்பு: (i) மேற்கண்ட நிரூபணத்தில் PR = SQ கூறுவது என்னவென்றால் ஒருவட்டத்தின் மீது இரண்டு புள்ளிகளுக்கிடையே உள்ள தொலைவு அதன்ஆரம் மற்றும் மையக் கோணத்தை கொண்டு தீர்மானிக்கப்படுகிறது.   

(ii) வில்கள் PR மற்றும் SQ ஆகியவை முறையே மையத்தில் தாங்கும் கோணம் α + βமற்றும் α + (-β) ஆகும். எனவே PR = SQ. எனவே (cos α,sin α) மற்றும் (cos (-β), sin( - β)) இக்கு இடைப்பட்ட தூரமும் (cos (α+ β), sin(α + β)) மற்றும் (1, 0) ஆகிய புள்ளிகளுக்கு இடைப்பட்ட தூரமும் சமம் ஆகும்.

(iii) மேலே உள்ள வருவித்தலில் 0 ≤ α <2 π, 0 ≤ β < 2π ஆகும். சைன் மற்றும் கொசைன் ஆகியவற்றின் சீர் சுழற்சித் தன்மையால் மேலே வருவித்த முடிவு எந்த ஒரு α மற்றும் β இக்கும் பொருந்தும்.

முற்றொருமை 3.2 : cos (α - β) = cos α cos β + sin α sin β

நிரூபணம் :

cos (α + β) = cos α cos β - sin α sin β என நமக்குத் தெரியும்,

இங்கு,       cos(α - β) = cos(α + (–β)] = cos α cos (-β) - sin α sin(-β) 

எனவே,      cos(α - β) = cos α cos β + sin α sin β

குறிப்பு: (i) மேலே உள்ள முற்றொருமையில் α = β எனப் பிரதியிடக் கிடைப்பது cos2 α + sin2 α = 1. 

(ii) α = 0 மற்றும் β = x எனப் பிரதியிடக் கிடைப்பது cos (- x) = cosx இது ஒரு இரட்டைச்சார்பு எனக் காட்டுகிறது.

முற்றொருமை 3.3 : sin(α + β) = sin α cos β + cos α sin β

நிரூபணம் :

sin(α + β) = cos[π/2 - (α + β) = cos [(π/2 - α)- β] 

என எழுதி மற்றும் முற்றொருமை 3.2-ஐ பயன்படுத்தி நிரூபிக்கலாம்.

குறிப்பு: α + β = π/2 எனில், மேலே உள்ள முற்றொருமை cos2 α + sin2 α = 1 என மாறும்.

முற்றொருமை 3.4 : sin(α - β) = sin α cos β - cos α sin β 

நிரூபணம் : 

sin(α – β) = sin [α + (–β)] என எழுதி மற்றும் முற்றொருமை 3.3ஐ பயன்படுத்தி நிரூபிக்கலாம். 

குறிப்பு: சைன் மற்றும் கொசைன் கூட்டல் மற்றும் கழித்தல் சூத்திரத்தை அணி அமைப்பில் எழுதலாம். 

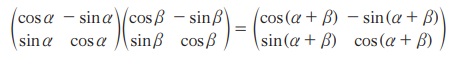
முற்றொருமை 3.5: tan(α + β) = tan α + tan β / 1 - tan α tan β

நிரூபணம் :

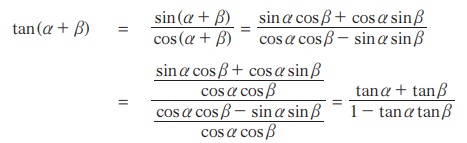
முற்றொருமை 3.6 : tan(α - β) = tan α - tan β / 1 + tan α tan β

நிரூபணம் :

tan(α - β) = tan[α + (-β)] 

என எழுதி மற்றும் முற்றொருமை 3.5 ஐ பயன்படுத்தி நிருபிக்கலாம்.

குறிப்பு: (i) தால்மி (CE 100-170) அவர்கள் கோணத்தின் நாணை முக்கோணவியல் சார்பாகக் கொண்டு ஒரு தேற்றத்தை நிரூபித்தார். ஒரு வட்ட நாற்கரத்தில் மூலைவிட்டங்களின் பெருக்கல் அதன் எதிர்ப்பக்கங்களின் பெருக்கலின் கூடுதலுக்குச் சமம். ABCD என்ற வட்ட நாற்கரத்தில்

(AC)(BD) = (AB) (CD) + (AD) (BC) ஆகும்.  

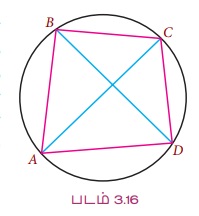
இதைப் பயன்படுத்திக் கூட்டல் மற்றும் கழித்தல் முற்றொருமைகளை நிரூபிக்கலாம். எனவே, இது தால்மியின் கூடுதல் மற்றும் வேறுபாடு சூத்திரம் ஆகும்.

(ii) பொதுவாக, cos (α ± β) ≠ cos α + cos β மற்றமுக்கோணவியல் சார்புகளுக்கும் இது பொருந்தும். 

(iii) α = β எனில், sin (α - β) = sin α cos β - cos α sin β இலிருந்து sin 0 = 0 எனக் கிடைக்கும். இது முன்பே கொடுக்கப்பட்ட ஒன்றாகும்.

(iv) α = π/2 மற்றும் β = θ எனில், sin (α - β) = sin α cos β - cos α sin β இலிருந்து sin(π/2 - θ) = cos θ எனக் கிடைக்கும். இது முன்பே நிரூபிக்கப்பட்ட ஒன்றாகும். 

(v) ஒரு கோணத்தை இரண்டு கோணங்களின் கூடுதலாகவோ அல்லதுவேறுபாடுகளாகவோ எழுதுவதன் மூலம் சில முக்கோணவியல் சார்புகளின் மதிப்பை நாம் காணலாம். எடுத்துக்காட்டாக tan 75°-ஐ மதிப்பிடுவதற்கு tan (45° + 30°) என்றும் அதுபோல் cos 135°-ஐ cos (180° - 45°) என எழுதி மதிப்பைக் காணலாம்.

எடுத்துக்காட்டு 3.15 மதிப்பு காண்க (i) cos 15° (ii) tan 165°. 

தீர்வு: 

(i) cos 15° = cos (45° - 30°) = cos 45° cos 30° + sin 45° sin 30°

எடுத்துக்காட்டு 3.16 sin x = 4/5 (முதல் காற்பகுதியில் உள்ளது) மற்றும் cos y =-12/13, (இரண்டாம் காற்பகுதியில் உள்ளது) எனில்,

(i) sin (x - y) (ii) cos(x - y) ஆகியவற்றைக் காண்க. 

தீர்வு:

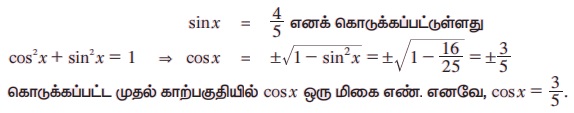
இதேபோல் இரண்டாம் காற்பகுதியில் cos y = -12 / 13 எனக் கொடுக்கப்பட்டுள்ளது

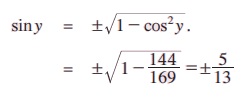
இரண்டாம் காற்பகுதியில் sin y ஒரு மிகை எண். எனவே, sin y = 5/13. 

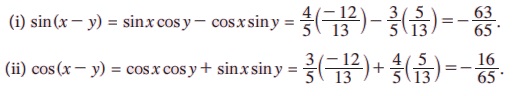
எடுத்துக்காட்டு 3.17 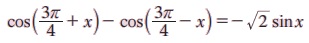என நிறுவுக.

தீர்வு :

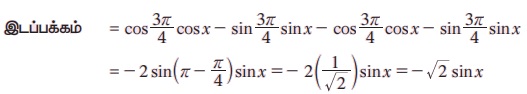
குறிப்பு: cos (A + x) - cos(A – x) = - 2 sin Asinx

எடுத்துக்காட்டு 3.18 நிறுவுக. A (9,12) என்ற புள்ளி தளத்தில் O ஐப் பொறுத்து இடஞ்சுழியாக 60° கோணத்தில் சுழலும்போது அடையும் புதிய நிலை B என்க, B இன் ஆயத்தொலைவுகளை காண்க.

தீர்வு:

A(9, 12) = A (rcosθ, rsinθ) இங்கு r = OA என்க 

எனவே, rcosθ = 9 மற்றும் rsinθ = 12 ஆகும்.

r2=81 + 144 = 225   ⇒  r = 15

எனவே, A என்பது A (15 cosθ, 15 sinθ) 

இங்கு, B என்பது B(15cos (θ + 60°), 15 sin(θ + 60°))

15 cos(θ + 60°) = 15(cosθ cos 60° – sinθ sin60°)

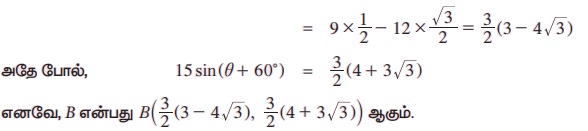
எடுத்துக்காட்டு 3.19 இரண்டு நீரலைகள் இணைவதை விளக்கும் அலைத்தொட்டி ஒன்று உள்ளது. h = 8cost மற்றும் h = 6 sint இங்கு t ∈ [0,2 π) என இரண்டு அலைகள் உள்ளன. இங்கு நேரம் t விகலைகளிலும், அலையா நீர்மட்டத்திலிருந்து அலையின் உயரம் மில்லி மீட்டரிலும் அளக்கப்படுகிறது என்க. கொடுக்கப்பட்ட இரு அலைகளும் இணையும்போது உருவாகும் அலையின் அதிகபட்ச உயரம் மற்றும் t இன் மதிப்பையும் காண்க.

தீர்வு:

t நேரத்தில் விளைவு அலையின் உயரம் H எனக் கொள்க.

 H = 8 cost + 6sint 

 8 cost + 6sint = kcos(t - a)

  = k(cos α cos α + sin t sin α) 

இங்கு ,  k = 10 மற்றும் tan α = 3/4 

எனவே,  H = 10 cos(t - a) 

  H-ன் மீப்பெரும் உயரம் = 10 மிமீ 

t = α எனும்போது மீப்பெரும் மதிப்பையடைகிறது. இங்கு tan α = 3/4

எடுத்துக்காட்டு 3.20 விரிவாக்குக. (i) sin(A + B + C) (ii) tan(A + B+ C).

தீர்வு:

(i) sin(A + B + C) = sin[A + (B + C)]

 = sin A cos (B + C) + cos A sin(B + C)

 = sin A cos B cos C + cos A sin B cos C + cos A cos B sinC – sin A sin B sin C

(ii) tan(A + B + C)     = tan[A + (B + C)]

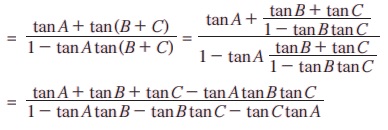
குறிப்பு: (i) A + B + C = 0 அல்லது π எனில், tan(A + B + C) = 0 மேலும் tan A + tanB + tan C = tanA tan BtanC

இம்முடிவு விரிகோண முக்கோணத்திற்கும் பொருந்தம். 

(ii) tan (x - y) + tan(y - z) + tan(z - x) = tan (x - y) tan(y - z) tan(z - x) 

(iii) tan 3A - tan 2A - tan A = tan 3A + tan(- 2A) + tan(- A) = tan 3A tan 2A tanA   

(iv) A + B + C = π /2 எனில் tanA tan B+ tan B tan C + tan C tan A = 1 (எப்படி?)

பயிற்சி 3.4

1. 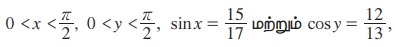எனில்

(i) sin (x + y) 

(ii) cos(x - y) 

(iii) tan (x + y) 

ஆகியவற்றின் மதிப்புகளைக் காண்க 

2. 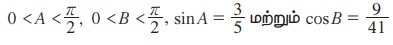எனில்

(i) sin (A + B) 

(ii) cos (A - B) ஆகியவற்றின் மதிப்புகளைக் காண்க. 

3. எனில் cos(x - y) இன் மதிப்பைக் காண்க.

4. 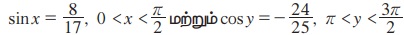எனில் sin(x - y) இன்மதிப்பைக் காண்க.

5. (i) cos 105° (ii) sin 105° (iii) tan 7π/12 ஆகியவற்றின் மதிப்புகளைக் காண்க. 

6. நிறுவுக: 

(i)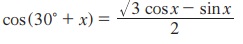

(ii) cos (π + θ) = - cos θ 

(iii) sin (π + θ) = - sin θ 

7. sin 15 மற்றும் cos 15° ஆகியவற்றை மூலங்களாகக் கொண்ட இருபடிச் சமன்பாட்டைக் காண்க. 

8. cos (A + B + C) ஐ விரிவாக்கு. இங்கு A + B + C = π/2  எனில்,

cos A cos B cos C = sin A sin B cos C + sin B sin C cos A + sin C sin A cos B என நிறுவுக. 

9. நிறுவுக (i) sin(45° + θ) – sin(45° - θ) = √2 sin θ

(ii) sin (30° + θ) + cos(60° + θ) = cos θ 

10. acos (x + y) = bcos (x - y) எனில் (a + b) tanx = (a - b)coty எனக் காண்பி. 

11. நிறுவுக. sin 105° + cos 105° = cos 45° 

12. நிறுவுக. sin 75° - sin 15° = cos 105° + cos 15°

13. நிறுவுக. tan 75° + cot 75° = 4

14. நிறுவுக. cos (A + B) cos C – cos (B + C) cos A = sin B sin (C - A) 

15. நிறுவுக. sin (n + 1) θ sin(n - 1) θ + cos(n + 1) θ cos(n - 1) θ = cos 2 θ, n ∈ Z. 

16. xcos θ = 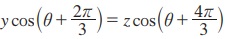எனில் xy + yz + zx இன் மதிப்பைக் காண்க 

17. நிறுவுக. 

(i) sin(A + B) sin(A - B) = sin2 A – sin2 B

(ii) cos(A + B)cos(A - B) = cos2 A – sin B = cos2 B – sin2 A 

(iii) sin2 (A + B) – sin2 (A – B) = sin 2A sin 2B 

(iv) cos 8 θ cos 2 θ = cos2 5 θ – sin2 3 θ

18. cos2 A + cos2 B - 2 cos A cos B cos(A + B) = sin2 (A + B) எனக் காண்பி

19. cos(α - β ) + cos(β - γ) + cos(γ - α) =- 3/2 எனில்

cos α + cos β + cosγ= sin α + sin β + sin γ = 0 எனக் காண்பி .

20. (i) tan(45° + A) =  1 + tan A/1 - tanA

(ii) tan(45° - A) = 1+ tan A /1 - tanA- எனக் காண்பி.

21. நிறுவுக. cot (A + B) = cot A cot B – 1/cot A + cotB

22. tanx =n/n+1=மற்றும் tany =1/2n+ 1எனில், tan (x + y) ஐக் காண்க

23. நிறுவுக. tan(π/4 + θ)tan(3 π/4 + θ)=- 1 

24. cot α =1/2 α ∈ (π, 3 π/2 ) மற்றும் sec β =-5/3, β∈( π/2, π ) எனில் tan(α + β) - இன்மதிப்பைக் காண்க.

25. θ + ϕ = α மற்றும் tan θ = k tan ϕ எனில், sin(θ - ϕ)  k - 1 / k +1sin α என நிறுவுக.

2. மடங்குக் கோண முற்றொருமைகள் மற்றும் உபமடங்குக் கோண முற்றொருமைகள் (Multiple angle identities and submultiple angle identities)

1831ஆம் ஆண்டு மைக்கேல் பாரடே (Michael Faraday) அவர்கள், ஒரு கம்பியை ஒரு காந்தத்தின் அருகே கொண்டு செல்லும்போது கம்பியில் சிறிதளவு மின்சாரம் உருவாகிறது என்பதைக் கண்டறிந்தார். இந்தப் பண்பு உலகம் முழுவதும் உள்ள வீடுகள், வியாபார நிறுவனங்கள், கல்விக்கூடங்கள், ஆகியவற்றிற்குத் தேவையான மின்சாரம் தயாரிக்கப் பயன்படுகிறது. ஆயிரக்கணக்கான கம்பிகளை மிகப்பெரிய மின்காந்தத்தைச் சுற்றிச் சுழற்றுவதால் மிக அதிகமாக மின்சாரம் தயாரிக்கப்படுகிறது.

மின்னழுத்தம் என்ற அளவை சைன் சார்பாகவும் வரைபடமாகவும் மாற்றலாம். தற்காலமின்சாரவியல் மற்றும் வேறு சில இயல்பான நிகழ்வுகளுக்கு முக்கோணவியல் சார்புகளையும் மற்றும் மடங்குக் கோணம் அல்லது உபமடங்குக் கோண முற்றொருமைகளைப் பயன்படுத்தலாம். 

A என்பது ஒரு கோணம் எனில், பிறகு 2A, 3A, ..., ஆகியவை A-ன் மடங்கு கோணங்கள் என்று கூறப்படும் மற்றும் A/2, A/3,…. ஆகியவை கோணங்கள் A-ன் உபமடங்கு கோணங்கள் என்றுகூறப்படும். இப்போது நாம் மடங்கு கோணங்கள் மற்றும் உபமடங்கு கோணங்களின் முக்கோணவியல் விகிதங்களை விவாதிப்போம் மற்றும் சில முற்றொருமைகளை தருவிப்போம்.

இருமடங்குக் கோண முற்றொருமைகள் (Double Angle Identities)

கூட்டல் மற்றும் கழித்தல் முற்றொருமைகளை எடுத்துக்கொண்டு அவற்றிலிருந்து வரக்கூடிய சில விளைவுகளைப் ஆராய்வோம். இருமடங்குக் கோண முற்றொருமைகள் கூட்டல் முற்றொருமையின் சிறப்பு அமைப்பாகும். இரண்டு கோணங்கள் சமம் எனில் கூட்டல் முற்றொருமை இருமடங்கு கோண முற்றொருமையாக மாறும். அவைகள் முக்கோணவியல் சமன்பாடுகளின் தீர்வு காணவும் மற்றும் முற்றொருமைகளை சரிபார்க்கவும் பெரிதும் பயன்படுகின்றன. இருமடங்குக் கோண முற்றொருமைகள் குறைப்பு முற்றொருமைகள் (அடுக்குக் குறைப்பு முற்றொருமைகள்) வருவிக்கப் பயன்படுகிறது. மேலும் முக்கோணவியல் கோவைகளின் மிகை மற்றும் குறை மதிப்புகளைக் காண இரு மடங்கு கோண முற்றொருமைகள் பயன்படுகிறது.

முற்றொருமை 3.7: sin 2A = 2sin A cos A 

நிரூபணம்

sin (α + β) = sin α cos β + cos α sin β என நமக்குத் தெரியும்.

α = β = A என எடுத்துக் கொள்க.

எனில், நமக்குக் கிடைப்பது, sin(A + A) = sin A cos A + sinA cos A 

எனவே, sin 2A = 2sin A cos A

குறிப்பு: (i) y = sin 2x மற்றும் y = 2 sinx ஆகியவை வெவ்வேறானவை. அவைகளின் வரைபடம் வரைந்து வித்தியாசத்தை உணரலாம்.

(ii) sin2A = 2 sin A cosA இன் பயன்பாடு: α எனும் திசைவேகத்தில் கிடைமட்டத்திற்கு u எனும் கோணத்தில் எறியப்பட்ட ஒரு பொருள், தரையிரங்குவதற்கு முன் அது பயணிக்கும் கிடைமட்ட தொலைவை அளவிடும் சூத்திரம் R = u2 sin2a /g.

α = π /4 எனும் போது R-ன் மீப்பெரும் மதிப்பு u2/g என்பது நமக்கு தெளிவாகிறது. 

(iii) | sin AcosA | = |sin2A/2| ≤ 1/2

A = π/4 எனும் போது sin A cosA-ன் மீப்பெரு மதிப்பு 1/2 ஆகும். எனவே, -1/2 ≤ sin A cos A ≤ 1/2.

எடுத்துக்காட்டு 3.21 ஒரு கால்பந்து விளையாட்டு வீரர் விளையாட்டுத்திடல் தரைமட்டத்திலிருந்து கால்பந்தை 80 அடி/விகலை தொடக்கத் திசைவேகத்துடன் உதைக்கிறார், பந்து அடையும் அதிகபட்சக் கிடைமட்டத் தூரத்தையும், பந்து உதைக்கப்பட்டு மேலே எழும்பும் போது கிடைமட்டத்துடன் அது ஏற்படுத்தும் கோணத்தையும் காண்க (g = 32 என்க). 

தீர்வு: 

கிடைமட்டத் தூரம் R காணப் பயன்படும் சூத்திரம்

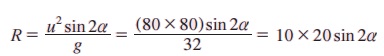
எனவே, அதிகபட்ச உயரம் = 200 அடி ஆகும். α = 45° எனும் கோணத்தில் உதைக்கும்போது பந்து அதிகபட்ச உயரத்தை அடையும்.

முற்றொருமை 3.8: cos 2A = cos2A – sin2A

நிரூபணம்

cos(α + β) = cos α cos β - sin α sin β என நமக்கு தெரியும்

α = β = A என எடுத்துக்கொள்க 

cos (A + A) = cos A cos A – sin Asin A

cos 2A = cos2 A – sin2 A எனக் கிடைக்கும்

குறிப்பு: cos 2A = cos2 A – sin2 A என்ற முற்றொருமையிலிருந்து

cos 2A = cos2 A - (1 – cos2 A) = 2 cos2 A – 1 மற்றும் 

cos 2A = (1 – sin2 A) – sin2 A = 1 – 2 sin2 A எனக் கிடைக்கிறது.

முற்றொருமை 3.9: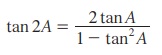

நிரூபணம்

முற்றொருமை 3.10 :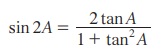

நிரூபணம்

sin 2 A = 2 sin A cos A என நமக்குத் தெரியும்

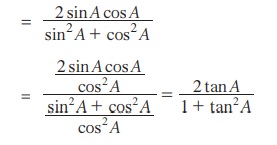
முற்றொருமை 3.11 :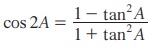  

நிரூபணம்

cos 2 A = cos2 A – sin2 A என நமக்குத் தெரியும்

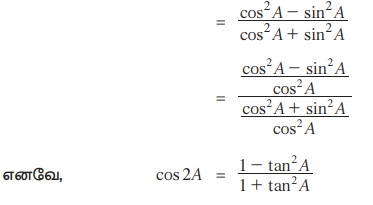
அடுக்குக் குறைப்பு முற்றொருமைகள் அல்லது குறைப்பு முற்றொருமைகள் (Power reducing identities or reduction identities)

இருமடங்குக் கோண முற்றொருமையிலிருந்து sine, cosine மற்றும் tangent இக்கான குறைப்பு முற்றொருமைகளைக் காணலாம். எடுத்துக்காட்டாக,

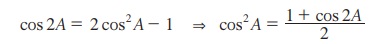
பின்வரும் அட்டவணையில் அடுக்குக் குறைப்பு முற்றொருமைகள் கொடுக்கப்பட்டுள்ளன.

குறிப்பு: (i) அடுக்குக் குறைப்பு முற்றொருமையில் அடுக்கு இரண்டிலிருந்து ஒன்றாகக் குறைக்கப்பட்டுள்ளது. 

(ii) அடுக்குக்குறைப்பு முற்றொருமைகள் sine மற்றும் cosine ஆகியவற்றின் இரட்டைப்படை அடுக்குகளை, அடுக்கு ஒன்றையுடைய cosine ஆக மாற்றப் பயன்படுகிறது. எடுத்துக்காட்டாக, அடுக்குக் குறைப்பு முற்றொருமைகளைப் பயன்படுத்தி,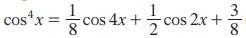மற்றும் 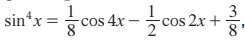என நிரூபிக்கலாம். (முயற்சி செய்!) 

(iii) உயர் கணிதத்தில் அடுக்குக் குறைப்பு முற்றொருமைகள் பெரிதும் பயன்படுகின்றன.

மும்மடங்குக் கோண முற்றொருமைகள் (Triple-Angle Identities)

இருமடங்குக் கோண முற்றொருமைகளைப் பயன்படுத்தி மும்மடங்குக் கோண முற்றொருமைகளைக் காணலாம்.

முற்றொருமை 3.12 : sin 3 A = 3 sin A – 4 sin3 A 

நிரூபணம்

sin 3 A = sin (2 A + A) = sin 2 A cos A + cos 2 A sin A 

= 2 sin A cos2 A + (1 - 2 sin2 A) sin A

= 2 sin A (1 – sin2 A) + (1 – 2 sin2 A) sin A

= 3 sin A - 4 sin3 A

முற்றொருமை 3.13 : cos 3 A = 4 cos3 A – 3 cos A

நிரூபணம்

cos 3 A = cos (2 A + A) = cos 2 A cos A - sin 2 A sin A

= (2 cos2 A – 1) cos A – 2 sin A cos A sin A

= (2 cos2 A – 1) cos A – 2 cos A (1 – cos2 A) 

= 4 cos3 A - 3 cos A

முற்றொருமை 3.14 : tan 3 A = 3 tan A - tan A / 1 – 3 tan A 

நிரூபணம்

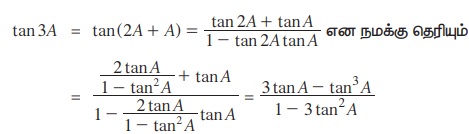
இருமடங்கு மற்றும் மும்மடங்குக் கோண முற்றொருமைகள் கீழே கொடுக்கப்பட்டுள்ளன

அரைக்கோண முற்றொருமைகள் (Half-angle identities)

அரைக்கோண முற்றொருமைகள் இருமடங்குக் கோண முற்றொருமைகளோடு தொடர்புடையவை. சிறப்புக் கோணங்களின் சரிபாதிக் கோணம் தேவைப்படும்போது அரைக்கோண முற்றொருமைகள் பயன்படுகின்றன.

எடுத்துக்காட்டாக, sin 15° ஆனது sin 15° = sin 30°/2 எனக் கொண்டு கணக்கிடவேண்டும். மேலும் அரைக்கோண முற்றொருமைகளைப் பயன்படுத்தி மிகச்சரியான மதிப்புகளைக் காணலாம்.

இருமடங்குக் கோண முற்றொருமைகளில் 2A = θ அல்லது A = θ / 2 எனப் பிரதியிட θ/2 கோணங்களுடைய புதிய முற்றொருமைகள் கிடைக்கும்.

அரைக்கோண முற்றொருமைகளை பின்வரும் அட்டவணையில் காணலாம்.

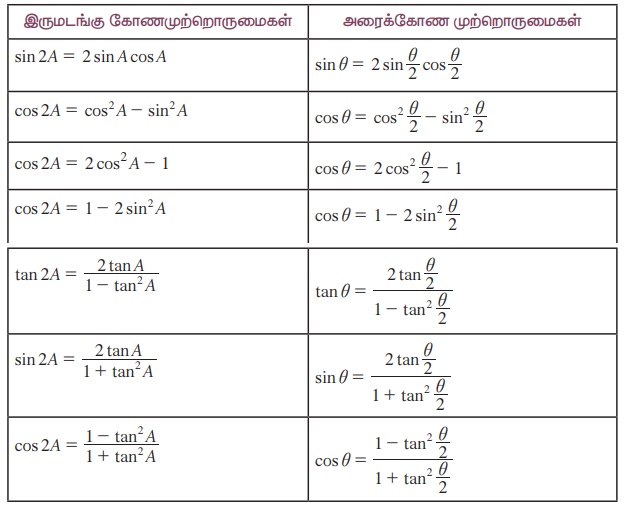
குறிப்பு: (i) வர்க்கப்படுத்தப்பட்ட முக்கோணவியல் சார்புகளை வர்க்கப்படுத்தாதமுக்கோணவியல் சார்பாக மாற்றுவதற்கு அரைக்கோணமுற்றொருமைகள்அதிகம் பயன்படுகின்றன. 

(ii) ஒரு கோணத்தின் cosine மதிப்பு கொடுக்கப்பட்டிருந்தால் அதன் அரைக்கோணத்தின் sine மற்றும் cosine மதிப்புகளைக் கண்டறிய அரைக்கோண முற்றொருமைகள் பயன்படுகின்றன.

எடுத்துக்காட்டு 3.22 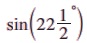இன் மதிப்பைக் காண்க.

தீர்வு:

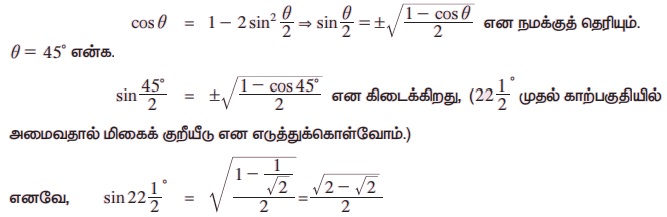
எடுத்துக்காட்டு 3.23 sin θ = 12/13, θமுதல் காற்பகுதியில் அமைகிறது எனில், sin 2θ இன் மதிப்பைக் காண்க. 

தீர்வு: 

ஒரு செங்கோண முக்கோணத்தைப் பயன்படுத்தி cos θ = 5/13, என்பதை எளிதாகக் காணலாம்.

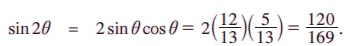
குறிப்பு: முக்கோணத்தை வடிவமைக்காமல் நாம் 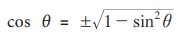எனும் கொசைன் சூத்திரத்தை பயன்படுத்தி cos θ மதிப்பைக் காணலாம்.

எடுத்துக்காட்டு 3.24 நிறுவுக. sin 4A = 4sinA cos3 A – 4 cos Asin3 A 

தீர்வு: 

4 sin A cos3 A – 4 cos A sin3 A = 4 sinA cos A (cos2 A – sin2 A)

 = 4 sinA cos A cos 2A = 2(2 sinA cos A) cos 2A

 = 2(sin 2A) cos 2A = sin 4A

எடுத்துக்காட்டு 3.25 நிறுவுக.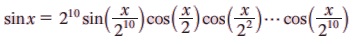

தீர்வு:

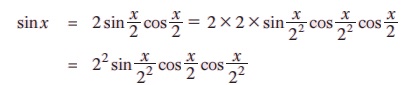
அரைக்கோண sine சூத்திரத்தை மீண்டும் மீண்டும் பயன்படுத்தினால் நமக்குக் கிடைப்பது,

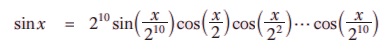
குறிப்பு: மேலே உள்ள முடிவானது எந்த முடிவுறு எண்ணிக்கைக்கும் நீட்டிக்க முடியும்.

எடுத்துக்காட்டு 3.26 நிறுவுக.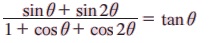

தீர்வு:

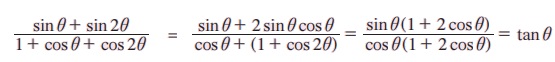
எடுத்துக்காட்டு 3.27 நிறுவுக.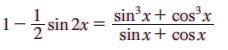

தீர்வு:

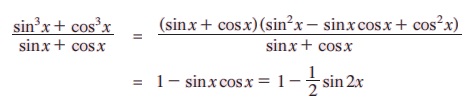
எடுத்துக்காட்டு 3.28 – π < x < π மற்றும் cos 2x = sinx எனில் x-இன் மதிப்புகளைக் காண்.

தீர்வு:

cos 2x = sinx என நமக்குத் தெரியும்.

எனில்,   2 sin2 x + sinx - 1 = 0 எனக் கிடைக்கிறது.

மேலே உள்ள சமன்பாட்டின் மூலங்கள் sinx = - 1 ±3/4 =- 1 அல்லது 1/2 ஆகும்.

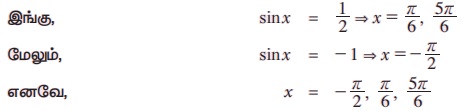
எடுத்துக்காட்டு 3.29 மதிப்புகளைக் காண்க.

(i) sin 18° (ii) cos 18° (iii) sin 72° (iv) cos 36° (v) sin 54° 

தீர்வு:

(i) θ = 18° என்க. 

இவ்வாறாக,       5θ = 90° 

3θ + 2θ = 90°     2θ = 90° - 3θ

 sin 2θ = sin(90° - 3θ) = cos 3θ 

 2sinθ cosθ = 4 cos3θ - 3 cosθ

 cos θ = cos 18° ≠ 0 ஆதலால் நமக்கு கிடைப்பது 

 2 sinθ = 4 cos2θ – 3 = 4(1 – sin2θ) – 3

4 sin2θ + 2 sinθ - 1= 0

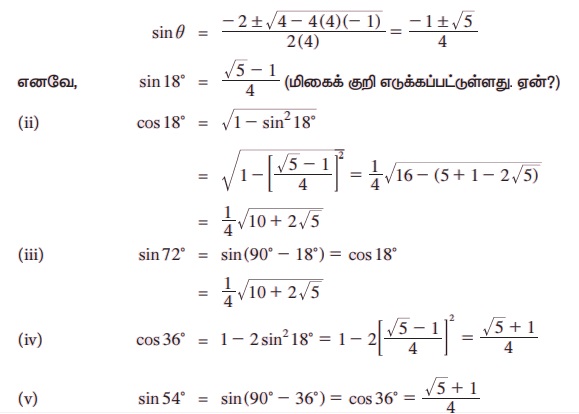
குறிப்பு: sin 18° = cos 72°, cos 18° = sin 72° மற்றும் cos 36° = sin 54° என கவனிக்கவும்.

எடுத்துக்காட்டு 3.30 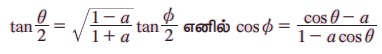என நிறுவுக.

தீர்வு:

அரைக்கோண முற்றொருமைகளின்படி நமக்குக் கிடைப்பது,

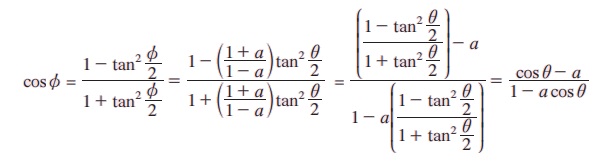
எடுத்துக்காட்டு 3.31 √3 cosec 20° - sec 20° இன் மதிப்பைக் காண்க. 

தீர்வு:

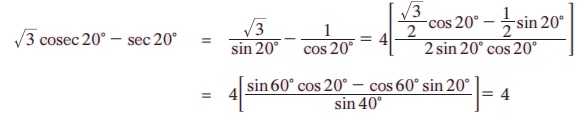
எடுத்துக்காட்டு 3.32 நிறுவுக.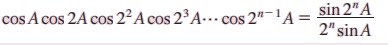

தீர்வு:

பயிற்சி 3.5

1. A முதல் காற்பகுதியில் இருக்கும் போது cos 2A-ன் மதிப்பைக் காண்க.

(i) cos A = 15/17

(ii) sin A = 4/5 

(iii) tan A = 16/63

2. θ ஒரு குறுங்கோணம் எனில்,

(i) sin θ = 1/25 எனும்போது sin (π/4-θ/2)

(ii) sinθ = 8/9 எனில் cos(π/4+ θ/2) ன் மதிப்புகளைக் காண்க.

3. எனக் காண்பி. 

4. cos 5θ = 16 cos5 θ - 20 cos3 θ+ 5 cosθ என நிறுவுக

5. 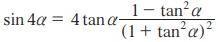என நிறுவுக.

6. A + B = 45° எனில், (1 + tan A)(1 + tan B) = 2 என நிறுவுக. 

7. (1 + tan 1°)(1 + tan 2°)(1 + tan 3°) ... (1 + tan 44°) என்பது 4 இன் மடங்கு என நிறுவுக. 

8. 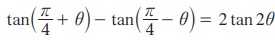என நிறுவுக. 

9. 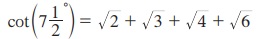எனக் காண்பி. 

10. (1 + sec 2 θ)(1 + sec 4 θ) … (1 + sec 2n θ) = tan 2n θ cot θ என நிறுவுக. 

11. 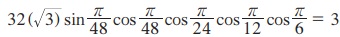என நிறுவுக.

3. பெருக்கலிலிருந்து கூட்டல் மற்றும் கூட்டலிலிருந்து பெருக்கல் முற்றொருமைகள் (Product to sum and sum to product identities)    

முக்கோணவியல் சார்புகளின் சில பயன்பாட்டின்போது முக்கோணவியல் சார்புகளின் பெருக்கலை முக்கோணவியல் சார்புகள் கூட்டல் அல்லது கழித்தலாக எழுத வேண்டிய தேவை ஏற்படுகிறது. சைன் மற்றும் சொசைனின் கூட்டல் மற்றும் கழித்தல் முற்றொருமைகள் நடுவில் இருக்கும் குறியைத் தவிர மற்றவைகள் ஒன்றுபோல் இருப்பது ஆச்சரியத்திற்குரியதாகும்.

இப்பண்பு அவற்றை இணைத்துப் புதிய முற்றொருமையை உருவாக்க ஏதுவாக உள்ளது. அதன் மூலம் பெருக்கலைக் கூட்டலாகவும், கூட்டலைப் பெருக்கலாகவும் மாற்றி எழுதக்கூடிய பல முற்றொருமைகள் கிடைக்கிறது. 

                        sin(A + B) = sinA cosB + cos A sinB           (3.1) 

                        sin(A – B) = sin A cos B - cos A sin B         (3.2) 

                        cos (A + B) = cos A cosB - sin AsinB          (3.3) 

                        cos(A - B) = cos A cos B + sin Asin B         (3.4) 

மேலேயுள்ள முற்றொருமைகளிலிருந்து நாம் எளிதாகப் பின்வரும் பெருக்கலிலிருந்து கூடுதல் முற்றொருமைகள் தருவிக்கலாம்.

          sin A cosB  = 1/2 [sin(A + B) + sin(A – B)]      (3.5)

                        cos AsinB   =1/2[sin(A + B) – sin(A – B)]        (3.6)

                        cos Acos B = ½ (cos (A + B) + cos(A - B)]      (3.7)

                        sin AsinB   =1/2(cos(A - B) - cos(A + B)]        (3.8)

sine மற்றும் cosine-களின் பெருக்கலைக் கூடுதலாக மாற்றி அமைக்க வேண்டிய அவசியம் தேவைபடும்போது மேற்கண்ட முற்றொருமைகள் அவசியமாகிறது. சில தொகையிடலை மதிப்பிடுவதற்கு இந்த யுக்தி பெரிதும் பயன்படுகிறது.

கூட்டலிலிருந்து பெருக்கல் முற்றொருமைக்கு, A + B = C மற்றும் A - B = D எனப் பிரதியிடலாம் அல்லது மேலும் அதற்குச் சமமான 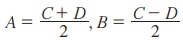இவற்றை முற்றொருமைகள் (3.5)2 இலிருந்து (3.8) வரை பிரதியிடவேண்டும். இதன் மூலம் பின் வருமாறு கூட்டலிருந்து பெருக்கலுக்கான முற்றொருமைகள் நமக்கு கிடைக்கின்றன. 

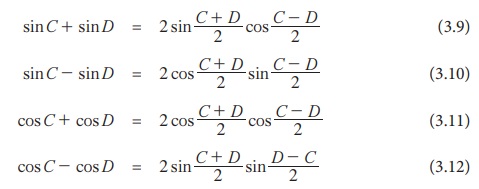
முற்றொருமை 3.15 : நிறுவுக. sin (60° - A) sin A sin (60° + A) = 1/4 sin 3A 

நிரூபணம் 

sin(60° - A) sin A sin(60° + A) = sin(60° - A)sin(60° + A) sin A

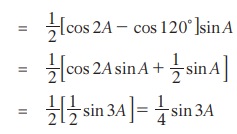
இதேபோல் பின்வரும் இரண்டு முக்கியமான முற்றொருமைகளை நாம் நிரூபிக்கலாம்

முற்றொருமை 3.16 : cos (60° - A) cos A cos (60° + A) = 1/4 cos 3A

முற்றொருமை 3.17: tan(60° - A)tan A tan (60° + A) = tan 3A

எடுத்துக்காட்டு 3.33 பின்வருவனவற்றைக் கூட்டல் அல்லது கழித்தலாகக் கூறு. (i) sin 40° cos 30° (ii) cos 110° sin 55°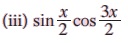

தீர்வு:

(i) 2 sin A cos B = sin(A + B) + sin(A - B) என நமக்குத் தெரியும்.

A = 40° மற்றும் B = 30° என்க.

2 sin40° cos 30°= sin(40° + 30°) + sin(40° - 30°) = sin70° + sin 10°

எனவே,             sin40° cos 30°= 1/2 (sin70° + sin 10°)

 (ii) 2 cos Asin B = sin(A + B) - sin(A - B) என நமக்குத் தெரியும்.

A = 110° மற்றும் B = 55° என்க.

2 cos 110° sin 55° = sin(110° + 55°) – sin(110° - 55°) எனக் கிடைக்கிறது.

எனவே ,      cos 110° sin 55° = 1/2 [sin 165° - sin55° ]

(iii) 2 sin A cosB = sin(A + B) = sin(A - B) என நமக்குத் தெரியும். 

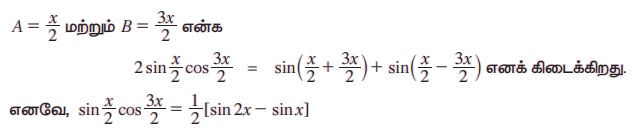
எடுத்துக்காட்டு 3.34 பின் வருவனவற்றை கூட்டல் மற்றும் கழித்தலைப் பெருக்கலாக கூறுக.

(i) sin 50° + sin 20° (ii) cos 6 θ + cos 2 θ (iii)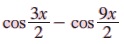

தீர்வு:

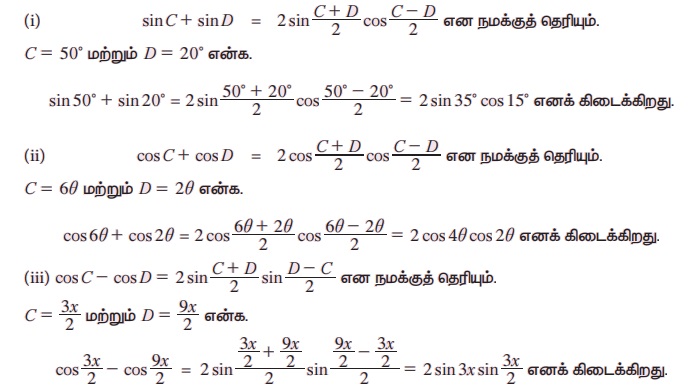
எடுத்துக்காட்டு 3.35 sin 34° + cos 64° – cos 4° இன் மதிப்பைக் காண்க. 

தீர்வு:

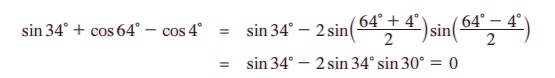
எடுத்துக்காட்டு 3.36 நிறுவுக. cos 36° cos 72° cos 108° cos 144° = 1/16

தீர்வு:

இடப்பக்கம் = cos36° cos(90° - 18°) cos (90° + 18°) cos (180° - 36°)

= sin2 18° cos2 36°

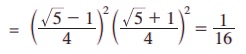
எடுத்துக்காட்டு 3.37 சுருக்குக.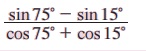

தீர்வு:

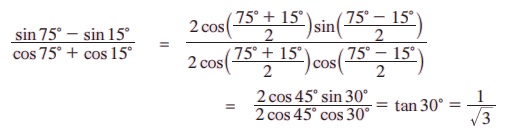
குறிப்பு: sin 75° = cos 15° மற்றும் cos 75° = sin 15° எனக் கொண்டு தீர்வு காண முயற்சி செய்க.

எடுத்துக்காட்டு 3.38 cos 10° cos 30° cos 50°cos 70° = 3/16 எனக் காண்பி.

தீர்வு:

cos (60° - A) cos A cos (60° + A) = 1/4 cos 3A என நமக்குத் தெரியும். 

cos 10° cos 30° cos 50° cos 70° = cos 30°[cos 10° cos 50° cos 70°]

                                                    = cos 30°[cos(60 - 10°) cos 10° cos(60° + 10°)]

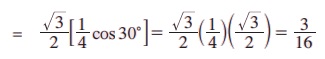
பயிற்சி 3.6

1. பின்வருவனவற்றைக் கூட்டல் அல்லது கழித்தலாக கூறுக. 

(i) sin 35° cos 28°

(ii) sin 4x cos 2x 

(iii) 2 sin 10 θ cos 2θ 

(iv) cos 5θ cos 2θ

(v) sin 5θ sin 4θ 

2. பின்வருவனவற்றைப் பெருக்கலாக கூறுக. 

(i) sin 75° – sin 35°

(ii) cos 65° + cos 15° 

(iii) sin 50° + sin 40° 

(iv) cos 35° - cos 75° 

3. sin 12° sin48° sin 54° = 1/8 எனக் காண்பி.

4. 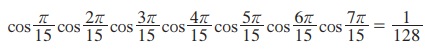எனக் காண்பி .

5. 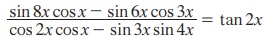எனக் காண்பி . 

6. 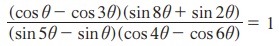எனக் காண்பி. 

7. நிறுவுக. sinx + sin 2x + sin 3x = sin 2x (1 + 2 cosx).

8. நிறுவுக.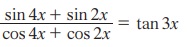

9. நிறுவுக. 1 + cos2x + cos4x + cos 6x = 4 cos.xcos 2x cos 3x 

10. நிறுவுக.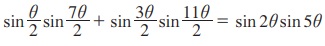

11. நிறுவுக. cos(30° - A)cos(30° + A) + cos (45° - A)cos(45° + A) = cos 2A + 1/4

12. நிறுவுக.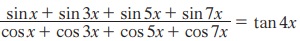

13. நிறுவுக .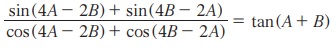

14. 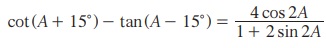எனக் காண்பி.

4. நிபந்தனைக்குட்பட்ட முக்கோணவியல் முற்றொருமைகள் (Conditional Trigonometric Identities)

கொடுக்கப்பட்ட கோணத்தின் அனைத்து ஏற்றுக்கொள்ளக்கூடிய மதிப்புகளுக்கும் முக்கோணவியல் முற்றொருமைகள் உண்மை என்பதை நாம் அறிவோம். சில முக்கோணவியல் முற்றொருமைகள் கொடுக்கப்பட்ட கூடுதல் நிபந்தனையையும் நிறைவு செய்கிறது. அப்படிப்பட்ட முற்றொருமைகள் நிபந்தனைக்குட்பட்ட முக்கோணவியல் சமன்பாடுகள் ஆகும். முன் பகுதிகளில் கண்ட தொடர்புகளின் அடிப்படையில் சில நிபந்தனைக்குட்பட்ட முக்கோணவியல் முற்றொருமைகளை இப்பகுதியில் பார்ப்போம்.

எடுத்துக்காட்டு 3.39 A + B + C = π எனில், பின்வருவனவற்றை நிறுவுக.

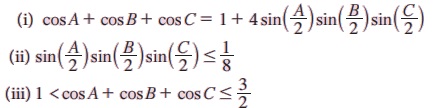
தீர்வு: 

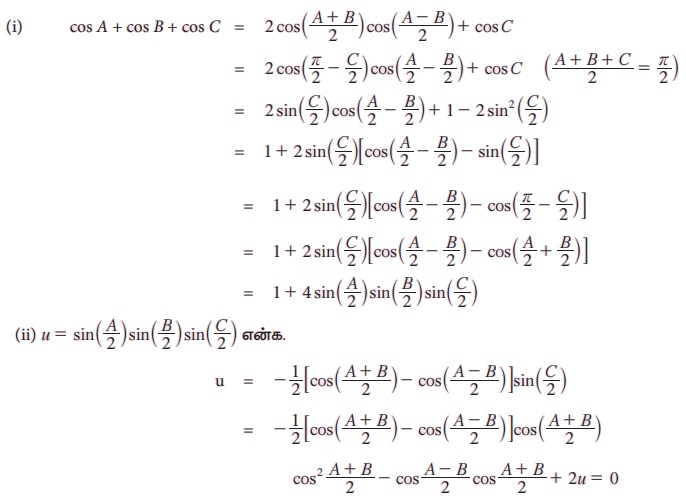
இது cos A+B/2 இன் இருபடிச்சமன்பாடாகும்.

cos A + B/2 ஒரு மெய்யெண் என்பதால் இச்சமன்பாட்டிற்குத் தீர்வு உண்டு. எனவே, தன்மைகாட்டி b2 - 4ac ≥ 0, தருவது யாதெனில்,

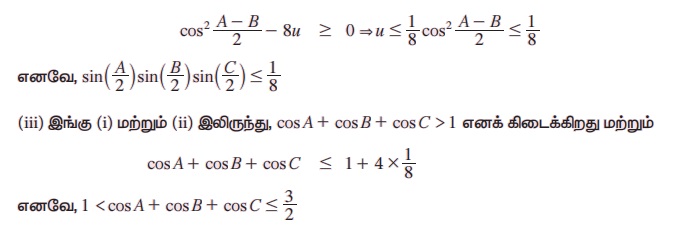
குறிப்பு: A + B + C = π எனில்,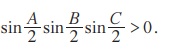

எடுத்துக்காட்டு 3.40 A + B + C = π எனில், 

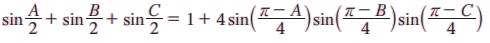என நிறுவுக. 

தீர்வு: 

-

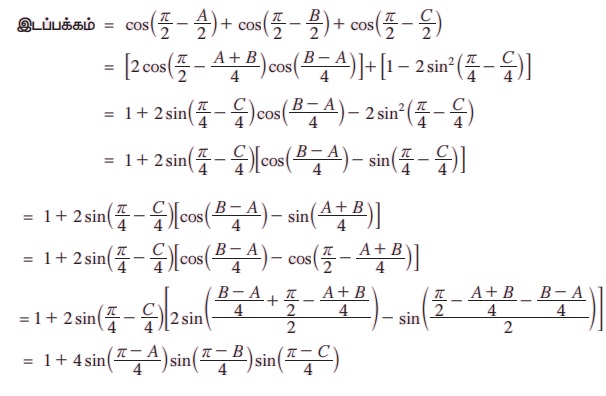
எடுத்துக்காட்டு 3.41 A + B + C = π எனில்,  cos2 A + cos2B + cos2 C = 1 – 2 cos A cos B cos C என நிறுவுக.

தீர்வு:

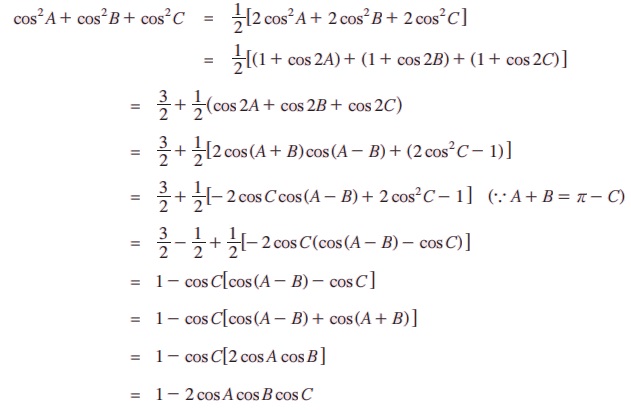
பயிற்சி 3.7

1. A + B + C = 180° எனில், பின்வருவனவற்றை நிறுவுக

(i) sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C 

(ii) cos A + cos B - cos C =- 1 + 4 cos A/2 cosB/2 sinC/2 

(iii) sin2 A+ sin2 B + sin2 C = 2 + 2 cos Ā cos B cos C 

(iv) sin2 A+ sin2 B – sin2 C = 2 sin A sin B cos C 

(v) tan A/2 tanB/2 + tanB/2 tanC/2 + tanC/2 tanA/2 = 1 

(vi) sin A + sinB + sin C =4 cosA/2 cos B/2cosC/2

(vii) sin(B + C - A) + sin(C + A - B) + sin(A + B - C) = 4 sin Asin B sin C

2. A + B + C = 25 எனில், sin(s – A) sin(s – B) + sin s sin(s – C) = sin Asin B என நிறுவுக.

3. x + y + z = xyz எனில், 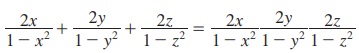என நிறுவுக.

4. A + B + C = π /2 எனில், பின்வருவனவற்றை நிறுவுக.

(i) sin 2A + sin 2B + sin 2C = 4 cos A cos B cosC

(ii) cos 2A + cos 2B + cos 2C = 1 + 4sinAsinBsinC 

5. ∆ ABC ஒரு செங்கோண முக்கோணம் மற்றும் ∠ A = π/2 எனில், பின்வருவனவற்றை நிறுவுக. 

(i) cos2 B + cos2 C = 1

(ii) sin2 B + sin2 C = 1 | 

(iii) cosB - cosc=-1+ 2 √2 cos B/2 sin C/2