முக்கோணத்தின் பண்புகள்

முக்கோணத்தின் பண்புகள் (Properties of Triangle)

ஒரு முக்கோணத்தால் வடிவமைக்கப்பட்ட செயல் முறை கூடிய பயன்பாட்டு கணக்குகளுக்குத் தீர்வு காண்பது முக்கோணவியலின் ஒரு முக்கியப் பயன்பாடாகும். ஒரு முக்கோணத்தின் அனைத்துப் பக்கங்களையும் மற்றும் கோணங்களையும் காண்பது முக்கோணத்தைத் தீர்க்கும் விதமாகக் குறிப்பிடப்படுகிறது. எந்தவொரு முக்கோணத்திலும் மூன்று பக்கங்கள் மற்றும் மூன்று கோணங்களை ஒரு முக்கோணத்தின் அடிப்படை உறுப்புகள் என்று அழைக்கிறோம். ஒரு செங்கோண முக்கோணத்தின் தீர்வு காண்பதில் பித்தாகரஸ் தேற்றம் பெரும் பங்காற்றுகிறது. ஒரு செங்கோணம் அல்லாத முக்கோணத்தைத் தீர்ப்பதில் சைன் மற்றும் கொசைன் விதிகள் திறம்பட பயன்படுத்தக்கூடிய முக்கியமான கருவிகள் ஆகும். இப்பிரிவில் ஒரு முக்கோணத்தின் மூன்று பக்கங்கள் மற்றும் மூன்று கோணங்களுக்கிடையே உள்ள தொடர்புகளை பற்றி விவாதிப்போம் மற்றும் சைன் மற்றும் கொசைன் விதிகளைத் தருவிப்போம். 

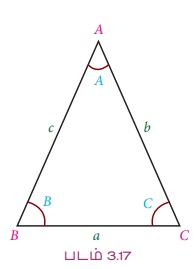
குறியீடு : ஒரு முக்கோணம் ABC என்க. ∆ABC இன் மூன்று முனைகள் A, B, C இன் கோணங்கள் A, B, C என்றே குறிக்கப்படுகிறது. A, B, C ஆகிய கோணங்களுக்கு எதிர் பக்கங்கள் முறையே a, b, c எனக் குறிக்கப்படுகின்றன. ∆என்ற குறியீடு முக்கோணத்தின் பரப்பைக் குறிக்கிறது. 

ஒருமுக்கோணத்தின் மூன்று முனைகளின் வழியாகச் செல்லக்கூடிய வட்டத்தை அதன் சுற்றுவட்டம் என்கிறோம். சுற்று வட்டத்தின் மையம் மற்றும் ஆரம் R ஆகியவை முறையே சுற்றுவட்ட மையம் மற்றும் சுற்றுவட்ட ஆரம் எனப்படும்.

குறிப்பு: ∆ABC இல், A + B + C = π மற்றும் a + b >c, b + c > a, a + c > b ஆகும்.