சைன் விதி அல்லது சைன் சூத்திரம்

சைன் விதி அல்லது சைன் சூத்திரம் (Law of sine or sine formula)

1. சைன் விதி (Law of sines)

ஒரு முக்கோணத்தின் கோணங்களுக்கும் மற்றும் பக்கங்களுக்கும் இடையே உள்ள தொடர்பே சைன் விதி ஆகும். ஓரு முக்கோணத்தை தீர்க்க, பின்வரும் சூழலில் சைன் விதியை திறம்பட பயன்படுத்தலாம்.

(i) இருபக்கங்கள் மற்றும் ஒரு கோணம் கொடுக்கப்பட்டால், கொடுக்கப்பட்ட இரு பக்கங்களுக்கிடையே உள்ள கோணம் இதில் சேர்க்கப்படவில்லை என்றால் மற்றைய கோணங்களைக் காணலாம்.

(ii) இரு கோணங்கள் மற்றும் ஒரு பக்கம் கொடுக்கப்பட்டு அது கொடுக்கப்பட்ட ஏதேனுமொரு கோணத்திற்கு எதிர்பக்கம் என்றால் மற்றைய பக்கங்களைக் காணலாம்.

தேற்றம் 3.1 (சைன் விதி) 

எந்த ஒரு முக்கோணத்திலும் பக்கங்களின் நீளங்கள் அவற்றிற்கு எதிரே உள்ள கோணங்களின் சைன் மதிப்பிற்கு நேர் விகிதத்தில் இருக்கும். இங்கு, ∆ ABC இல், 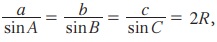இங்கு, R என்பது முக்கோணத்தின் சுற்றுவட்ட ஆரம் ஆகும்.

நிரூபணம் :

∆ABC இல் A என்ற கோணம் குறுங்கோணமாகவோ அல்லது செங்கோணமாகவோ அல்லது விரிகோணமாகவோ இருக்கலாம். இங்கு O என்பது ∆ABC -இன் சுற்றுவட்ட மையம் எனவும் மற்றும் R என்பது ஆரம் எனவும் கொள்வோம்.

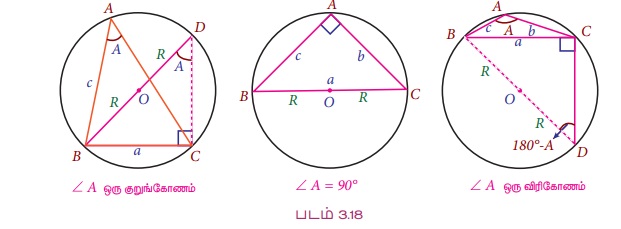
நிலை I

∠A, ஒரு குறுங்கோணம் 

BO ஐ நீட்டும் போது வட்டத்தின் மீது D என்ற புள்ளியை சந்திக்கின்றது.

∠BDC = ∠BAC = A

∠BCD = 90° 

நிலை II

∠A, ஒரு செங்கோணம் 

இந்நிலையில் O என்பது ∆ ABC இல் உள்ள BC -இன் பக்கம் மீது அமையும்.

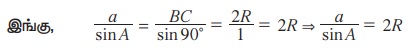
நிலை III

∠A, ஒரு விரிகோணம் 

BO ஐ நீட்டும்போது வட்டத்தில் D என்ற புள்ளியைச் சந்திக்கின்றது.

∠BDC + ∠BAC = 180°

∠BDC = 180° - ∠BAC = 180° - A

∠BCD = 90°

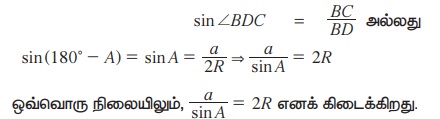
இதைப்போன்று கோணங்கள் B மற்றும் C ஆகியவற்றைக் கருத்தில் கொண்டால், 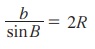மற்றும் 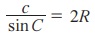என்பனவற்றை நிரூபிக்கலாம். எனவே,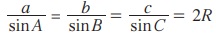

குறிப்பு: (i) சைன் விதியை மூன்று சமன்பாடுகளின் தொகுப்பாக எழுதலாம்.

(ii) சைன் விதியின்படி ஒரு முக்கோணத்தின் பக்கங்கள் அவைகளுக்கு எதிரேஉள்ள கோணங்களின் சைன் மதிப்பிற்கு நேர்விகிதத்தில் அமையும். 

(iii) ஒரு முக்கோணத்தின் இரு பக்கங்களும் அவற்றிற்கிடைப்பட்ட கோணமும்கொடுக்கப்பட்டிருந்தால் சைன் விதியைப் பயன்படுத்தி முக்கோணத்தின் தீர்வு காண இயலாது. 

(iv) ஒரு முக்கோணத்தின் மிகப்பெரிய பக்கம், மிகப்பெரிய கோணத்திற்கு எதிரே அமையும் என்பது சைன் விதியின் சுவாரஸ்யமான வடிவகணித விளைவாகும். (நிரூபி)

நேப்பியரின் சூத்திரம் 

தேற்றம் 3.2 

∆ABC இல்

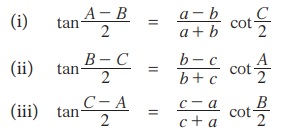
நிரூபணம் :

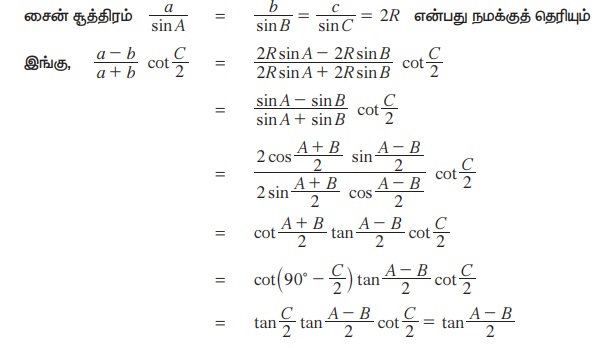
இதேபோன்று, மற்ற இரு சூத்திரங்களையும் நிரூபிக்கலாம்.

2. கொசைன் விதி (Law of Cosines)

ஒரு முக்கோணத்தின் இரண்டு பக்கங்களும் அவற்றிடைப்பட்ட கோணமும் அல்லது முக்கோணத்தின் மூன்று பக்கங்கள் கொடுக்கப் பட்டிருந்தால் சைன் விதியைப் பயன்படுத்தி அம்முக்கோணத்தைத் தீர்க்க இயலாது. அச்சமயங்களில் கொசைன் விதியைப் பயன்படுத்தி முக்கோணத்தின் தீர்வைக் காணலாம். மேலும், இது இரண்டு பக்கங்களும் மற்றும் இடைப்பட்ட கோணமும் கொடுக்கப்பட்டால் முக்கோணத்தின் பரப்பைக் காணும் சூத்திரத்தை வருவிக்கப் பயன்படுகிறது.

தேற்றம் 3.3 (கொசைன் விதி) 

∆ABC இல்,

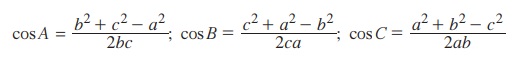
நிரூபணம் : 

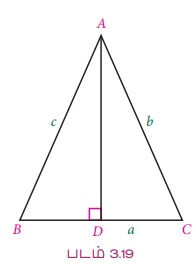
∆ABC இல் AD ⊥ BC என வரைக. 

∆ABD இல் AB2 = AD2 + BD2 = c2 = AD2 + BD2

∆ABC இன் உறுப்புகளின் மூலம் AD மற்றும் BD இன் மதிப்புகளைக் காணலாம்.

AD/AC = sin C  ⇒ AD = b sin C 

BD = BC – DC = a – b cos C 

c2 = (bsin C)2 + (a - bcos C)2

= b2 sin2 c + a2 + b2 cos2 C - 2ab cos C 

= a2 + b2 (sin2 C + cos2 C) – 2 ab cos C 

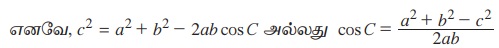
இதேபோன்று, மற்ற இரு சூத்திரங்களையும் நிரூபிக்கலாம். அவையாவன,  

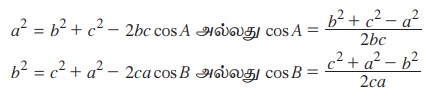
குறிப்பு: (i) a2 = b2 + c2 - 2bc cos A என்பது ஒரு முக்கோணத்தின் ஒரு பக்கத்தின் வர்க்கம் மற்ற இரண்டு பக்கங்களின் வர்க்கங்களின் கூடுதலிலிருந்து அவைகளின் பெருக்கட்பலனின் இருமடங்கை அவ்விரு பக்கங்களுக்கு இடைப்பட்ட கோணத்தின் கொசைன் மதிப்போடு பெருக்கக் கிடைக்கும் மதிப்பைக் கழிக்கக் கிடைக்கும் மதிப்புக்குச் சமம். மேலும் a, b, c ஆகிய எழுத்துக்களை ஒரு சூத்திரத்தில் சுழற்றும் போது மற்றொரு சூத்திரம் கிடைக்கப் பெறுகிறது.

(ii) ஒரு செங்கோண முக்கோணத்திற்கு கொசைன் விதியை எழுதும்போது அதுபித்தாகரஸ் தேற்றமாகக் குறைகிறது. எனவே, கொசைன் விதியைப் பித்தாகரஸ்தேற்றத்தின் பொதுமையாக்கப்பட்ட தேற்றமாகக் பார்க்கலாம். 

(iii) குறுங்கோணம் மற்றும் விரிகோணம் ஆகியவற்றில் கொசைன் சார்புகள்சைன் சார்பைப் போல் அல்லாமல் வித்தியாசமானவை என்பதால் சைன் விதியோடு ஒப்பிடும்போது கொசைன்விதியைப் பயன்படுத்துவது பயனுள்ளதாக இருக்கும். கோணத்தின் கொசைன் மதிப்பு மிகை எனில் அது குறுங்கோணம் இல்லையேல் அது விரிகோணம் ஆகும்.   

(iv) கொசைன் விதியின் பொருள்: நேர்வழித்தடம் குறைந்த தூரத்தையுடையது. இதன் விளக்கம் பின்வருமாறு. 

∆ABC இல், c2 = a2 + b2 - 2ab cosC, - cos C < 1 என்பதிலிருந்து நமக்கு c2 <a2 + b2 + 2ab என கிடைக்கிறது. எனவே, c < a + b. ஆகவே, ∆ABC இல், a < b + c , b < c + a, c < a + b எனக் கிடைக்கிறது. 

(v) கொசைன் விதியைப் பயன்படுத்தும் போது முதலில் அறியப்படாத அளவீட்டில் பெரிய கோணத்தைக் கண்டறிவது உத்தமம். இப்படியொரு கோணம் இருக்குமேயானால் அது முக்கோணத்தின் விரிகோணம் ஆகும்.

3. வீழல் சூத்திரம் (Projection Formula)

தேற்றம் 3.4 

∆ABC இல் நமக்குக் கிடைப்பது, 

(i) a = bcos C+ c cosB 

(ii) b = c cos A + acosC

(iii) c = acos B + bcos A

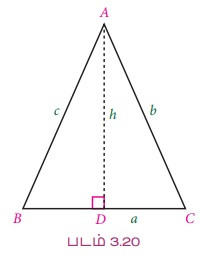
நிரூபணம் :

∆ABC இல் நமக்குக் கிடைப்பது, a = BC 

AD ⊥ BC ஐ வரைக.

a = BC = BD + DC

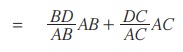
= (cos B)c + (cos C)b 

a  = b cos C + c cos B

இதேபோல், மற்ற இரு வீழல் சூத்திரங்களையும் நிரூபிக்கலாம்.

குறிப்பு: a = b cos C + c cos B என்பது, a = a இன் மீது b இன் வீழல் + a இன் மீது c இன் வீழல் ஆகும். எனவே, ஒரு முக்கோணத்தின் ஒரு பக்கத்தின் நீளம் அதன் மீது மற்ற இரு பக்கங்களின் வீழல்களின் கூடுதலுக்குச் சமம்.

4. முக்கோணத்தின் பரப்பளவு (Area of the triangle)

விரிகோண முக்கோணத்தின் சில உறுப்புகள் மற்றும் சைன் சார்பு ஆகியவற்றைப் பயன்படுத்தி முக்கோணத்தின் பரப்பளவைக் காணலாம். அடிப்பக்கம் b மற்றும் உயரம் h-ஐ கொண்ட ஒரு முக்கோணத்தின் பரப்பளவை காணும் சூத்திரம், 1/2 bh என்பதை நாம் நினைவூட்டுவோம்.

விரிகோண முக்கோணத்தில் பரப்பளவு சூத்திரத்தைப் பயன்படுத்துவதற்கு முன் உயரம் h-ன் மதிப்பை நாம் காணவேண்டும்.

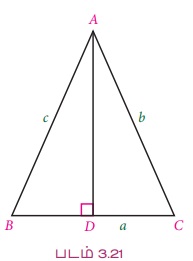
தேற்றம் 3.5

∆ABC இல், முக்கோணத்தின் பரப்பு 

∆ = 1/2ab sin c = 1/2 bc sin A = 1/2 ac sin B 

நிரூபணம் :

∆ABC இல், AD ⊥ BC என வரைக.

∆ADC இல், AD/AC = sin C ⇒ AD = bsinc 

எனவே, ∆ = ½ × அடிப்பக்கம் × உயரம் = 1/2 ab sin C 

இதே முறையில் மற்ற இரண்டு முடிவுகளைக் நிருபிக்கலாம். 

குறிப்பு: (i) விரிகோண முக்கோணத்தின் பரப்பளவு காணும் சூத்திரம் கூறுவது யாதெனில் இரண்டு பக்கங்களின் நீளங்கள் மற்றும் அவற்றிற்கு இடைப்பட்ட கோணத்தின் சைன் மதிப்பு ஆகியவற்றின் பெருக்கட்பலனில் பாதியாகும். 

(ii) வட்டத் துண்டின் பரப்பளவைக் காண முக்கோணத்தின் பரப்பளவு சூத்திரம் பயன்படுகிறது. வட்டத்துண்டு என்பது ஒரு நாணிற்கும் அது வெட்டும் வில்லிற்கும் இடைப்பட்ட பகுதி ஆகும். 

r என்பது வட்டத்தின் ஆரம் மற்றும் θ என்பது வட்டநாண் AB மையத்தில் தாங்கு கோணம் என்க.

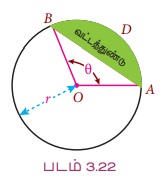
வட்டத்துண்டு ABD இன் பரப்பு = வட்டக் கோணப்பகுதியின் பரப்பு - ∆OAB இன் பரப்பு

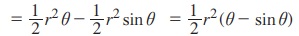
(iii) ஒரு செங்கோண முக்கோணத்தின் பரப்பு காணும் சூத்திரத்தின் பொதுமையாக்கப்பட்ட சூத்திரமாக முக்கோணத்தின் பரப்பளவு காணும் சூத்திரத்தைப் பார்க்கலாம்.

(iv) மேற்கண்ட சூத்திரத்திலிருந்து, முக்கோணங்களின் பரப்பளவைக் காண்பதற்கு மூன்றாவது பக்கத்தின் அளவு தேவையில்லை எனத் தெளிவாகிறது. மேலும், ஒரு முக்கோணத்தின் பரப்பளவைக் காண அதனுடைய உயரத்தைக் காண வேண்டிய அவசியமில்லை.

எடுத்துக்காட்டு 3.56 8 கி.மீ. விட்டமுள்ள வட்ட வடிவ மிருகக்காட்சி பூங்கா ஒன்றை அமைக்க அரசு திட்டமிடுகிறது. கால்நடை மருத்துவமனை அமைக்க 4 கி.மீ. நிளமுடைய வட்ட நாண் கொண்ட வட்டத்துண்டு தனியாக ஒதுக்கப்படுகிறது. கால்நடை மருத்துவமனை அமைக்க ஒதுக்கப்பட்ட வட்டத்துண்டின் பரப்பைக் காண்க.

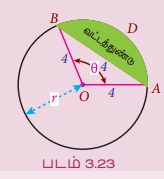
தீர்வு:

O ஐ மையமாகக் கொண்ட வட்டத்தின் நாண் AB என்க. 

∠AOB = θ என்க.

வட்டத்துண்டின் பரப்பு = வட்டக் கோணப் பகுதியின் பரப்பு - ∆OAB இன் பரப்பு

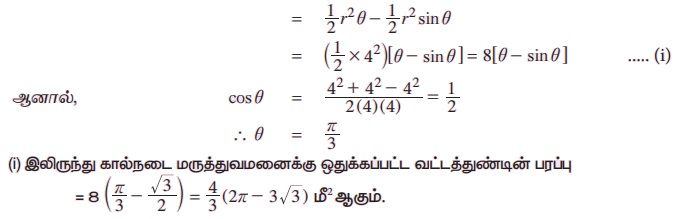
5. அரைகோண சூத்திரங்கள் (Half-Angle Formula) 

தேற்றம் 3.6 

∆ABC இல்,

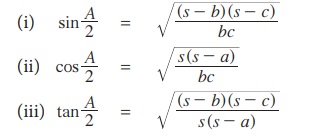
இங்கு, s என்பது ∆ABC இன் அரை சுற்றளவு, அதாவது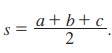

நிரூபணம் :

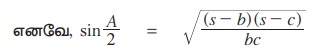
இதே போன்று மற்ற இரு முடிவுகளையும் நிருபிக்கலாம். 

குறிப்பு: மற்ற அரைக்கோண சூத்திரங்கள்

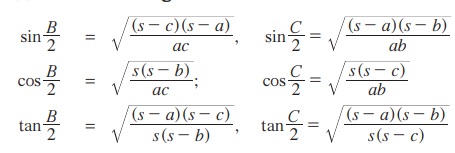
கிளைத்தேற்றம் :