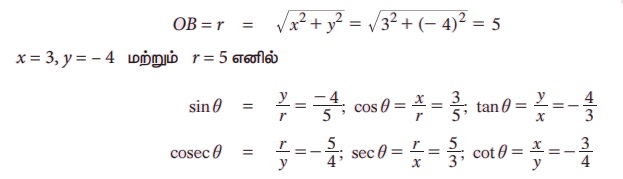முக்கோணவியல் சார்புகளும் மற்றும் அதன் பண்புகளும்

முக்கோணவியல் சார்புகளும் மற்றும் அதன் பண்புகளும்

(Trigonometric Functions and their Properties) 

1. கார்டீசியன் ஆயத்தொலை வடிவில் ஏதேனுமொரு கோணத்திற்கு முக்கோணவியல் சார்புகள் (Trigonometric Functions of any angle in terms of Cartesian Coordinates)

முக்கோணவியல் விகிதங்களுக்கான கொள்கைகளைக் கீழ் வகுப்புகளில் நாம் பயின்றோம். அது குறுங்கோண அளவில் மட்டுமே இருந்தது. ஆனால் நாம் குறுங்கோணம் அல்லாத பல கோணங்களைக் பார்த்துள்ளோம். நாம் குறுங்கோணத்தை நீட்டித்து மற்றும் முக்கோணவியலின் சார்புகளை ஏதேனும் ஒரு கோணத்திற்கு வரையறை செய்வோம். ஏதேனுமொரு கோணத்தின் முக்கோணவியல் விகிதங்களை ஆரையன் வடிவில் தரும்போது அவற்றை முக்கோணவியல் சார்புகள் என்கிறோம்.

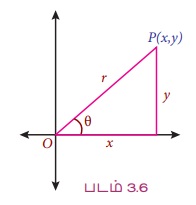
திட்ட நிலையில் θ-ன் முனையப் பக்கத்தில் ஆதியைத் தவிர வேறு ஒரு புள்ளி P(x, y) என்க. OP = r என்க.

இதனால்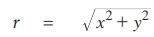

பின்வருமாறு θ -ன் ஆறு முக்கோணவியல் சார்புகள் வரையறுக்கப்பட்டுள்ளன.

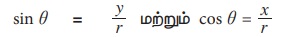
இதைப் பயன்படுத்தி மற்ற சார்புகளையும் காணலாம்.                   

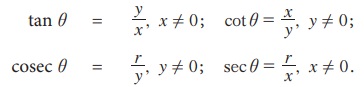
குறிப்பு: (i) | x | < r, | y | < r எனவே | cos θ | ≤ 1 மற்றும் | sin θ | ≤ 1. 

(ii) கோணம் குறுங்கோணமாக இருப்பின், மேலே குறிப்பிட்ட வரையறைகள் செங்கோண முக்கோணத்தை அடிப்படையாகக் கொண்ட வரையறைகளுக்குச் சமமாகும். 

(iii) P (x, y) ஐ தன்னகத்தே கொண்ட (கோணத்தை உருவாக்கும் முனைய பக்கம் எந்தக் காற்பகுதியில் இருக்கும் என்பதைப் பொறுத்து முக்கோணவியல் சார்புகளின் குறி (மிகை அல்லது குறை) அமையும். 

(iv) மேலே கொடுக்கப்பட்ட முக்கோணவியல் சார்புகளின் வரையறைகள் கோணத்தின் முனையப் பக்கத்தின் மீது உள்ள புள்ளியைச் சார்ந்திருக்காது (சரிபார்க்க!)

காற்பகுதிக் கோணங்களின் முக்கோணவியல் விகிதங்கள் (Trigonometric ratios of Quadrantal angles)

திட்ட நிலையில் கோணத்தின் முனையப்பக்கம் ஏதேனும் ஒரு அச்சோடு இணைந்திருந்தால் அக்கோணத்தைக்காற்பகுதிக் கோணங்கள் என்போம். காற்பகுதிக் கோணங்களின் முக்கோணவியல் விகிதங்களைக் காண்போம். 

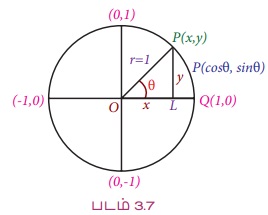
x2 + y2 = 1 என்ற சமன்பாட்டை உடைய ஓரலகு வட்டத்தைக் கருத்தில் கொள்க. θ-ன் முனைய பக்கம் ஓர் அலகு வட்டத்தின் மீது எங்குச் சந்திக்கிறதோ அப்புள்ளியை P (x, y) எனக் கொள்க.

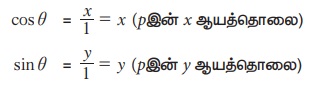
எனவே, ஓரலகு வட்டத்தில் ஏதேனுமொரு புள்ளி P (x, y) இன் ஆயத்தொலைவுகள் P(cos θ, sin θ) ஆகும். இவ்வகையில் கோண அளவை θ-ஆனது ஓரலகு வட்டத்தின் மீது உள்ள புள்ளியுடன் தொடர்புடையது.

மேலே உள்ள விளக்கத்தைப் பயன்படுத்தி எவ்வாறு காற்பகுதிக்கோணங்களில் முக்கோணவியல் சார்புகளின் மதிப்புகள் தீர்மானிக்கப்படுகிறது என்பதை பின்வரும் அட்டவணை விளக்குகிறது.

காற்பகுதிக் கோணங்களின் முக்கோணவியல் சார்புகளின் மிகச் சரியான மதிப்பு

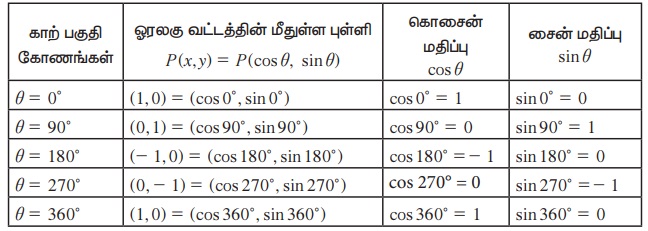
குறிப்பு: (i) ஓரலகு வட்டத்தின் மீதுள்ள எல்லாப் புள்ளிகளில் x மற்றும் y-ன் ஆயத்தொலைகள் - 1 மற்றும் 1-க்கு இடையே இருக்கும் என்பது குறிப்பிடத்தக்கது. எனவே θ - ன் மதிப்பு எதுவாகயிருந்தாலும் – 1 ≤ cos θ ≤ 1, - 1 ≤ sin θ ≤ 1 ஆகும்.

(ii) θ = 360° எனில் அது ஒரு முழு வட்டச் சுழற்சியாகும். அப்போது முனையப் பக்கம் மிகை x அச்சோடு இணைந்திருக்கும். எனவே, 0° மற்றும் 360° இல் சைனானது ஒரே மதிப்பைப் பெறும். இதனைப்போன்றே கொசைன் மற்றும் மற்றைய முக்கோணவியல் சார்புகளும் பின்பற்றுகிறது. 

(iii) இரண்டு கோணங்களின் வித்தியாசம் 360° அல்லது 2π - இன் முழு எண் மடங்காக இருப்பின் ஒவ்வொரு முக்கோணவியல் சார்பும் இரண்டு கோணங்களில் சம் மதிப்புகளைக் கொண்டிருக்கும்.

(iv) காற்பகுதிக்கோணத்தின் சைன் மற்றும் கொசைன்மதிப்புகளைக் பயன்படுத்தி வடிவக் கணித ரீதியில் பொதுமைப்படுத்திக் கீழே கொடுக்கப்பட்டுள்ளது.

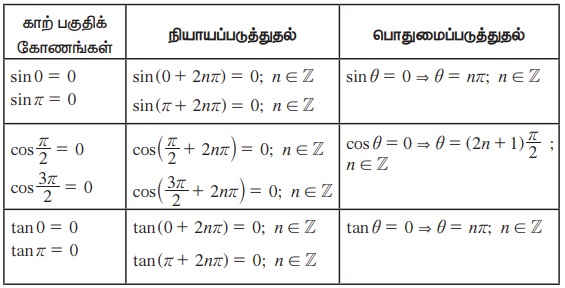
(v) cos θ = 0 எனும்போது tan θ ஐ வரையறுக்க இயலாது. எனவே, θ = 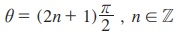என்னும்போது tan θ ஐ வரையறுக்க இயலாது.

2. மெய்யெண்களின் முக்கோணவியல் சார்புகள் (Trigonometric functions of real numbers)

நுண்கணிதம் உட்பட உயர் கணிதவியல் கணக்குகள், இயற்பியல் மற்றும் வேதியியல் கணக்குகள் ஆகியவற்றிற்கு முக்கோணவியலைப் பயன்படுத்த விஞ்ஞானிகளுக்கு மெய்யெண்களின் முக்கோணவியல் சார்புகள் தேவைப்பட்டது. இதற்காக ஓரலகு வட்டத்தின் மையக் கோணத்தை வில்லின் நீளத்தோடு தொடர்புபடுத்தப்பட்டது.

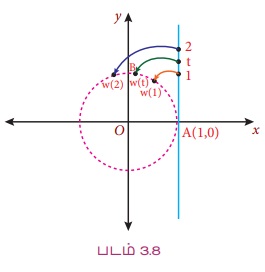
ஆதியை மையமாகக் கொண்ட ஓரலகு வட்டத்தைக் கருத்தில் கொள்க. ஓரலகு வட்டத்தின் மீதுள்ள புள்ளி A(1,0) என்பது பூச்சியக் கோணத்தை (ஆரையன் அளவில்) கொண்டது. A(1,0) இல் ஓரலகு வட்டத்திற்கு ஒரு தொடுகோடு வரைக. t ஒரு மெய்யெண் என்றிருக்கும்படி தொடுகோட்டின் மீதுள்ள ஒரு புள்ளியின் y அச்சுத் தூரம் t என்க.

ஒவ்வொரு மெய்யெண் t இக்கும் ஓரலகு வட்டத்தின் மீது வில் AB இன் நீளம் t என அமையும்படி B (x, y) என்ற புள்ளியைக் காண்க. t ஒரு மிகை எண் எனில் இடஞ்சுழி சுற்றில் B (x, y) ஐ தேர்வு செய்யவேண்டும். இல்லையெனில், வலஞ்சுழி சுற்றுத் திசையில் தேர்வு செய்ய வேண்டும். வில் AB மையத்தில் தாங்கும் கோணம் θ என்க. இம்முறையில் ஓரலகு வட்டத்தின் மீதுள்ள புள்ளிக்கு மெய்யெண் t -வுடன் தொடர்புடைய w(t) என்ற சார்பு பெறப்படுகிறது. இதைப் போர்த்தும் சார்பு (Wrapping Function) என்போம். மேலும் s = r θ எனும் போது வில்லின் நீளம் t = θ என பெறப்படுகிறது.

இங்கு, sin t = sin θ மற்றும் cos t = cos θ என்றும் வரையறுப்போம்.

sin t = sin θ = y மற்றும் cos t = cos θ = x, என்பது தெளிவாகிறது. 

மற்ற முக்கோணவியல் சார்புகளை sin t மற்றும் cos t ஆகியவற்றைப் பயன்படுத்தி மெய்யெண்களின் சார்புகளாக வரையறுக்க முடியும்.

குறிப்பு: (i) B (x, y) = B (cos t, sin t) என்ற புள்ளி ஓரலகு வட்டத்தின் மீதுள்ளது. எனவே, ஏதேனுமொரு t -க்கு – 1 ≤ cos t ≤ 1 மற்றும் – 1 ≤ sin t ≤ 1.  

(ii) ஒரு வட்டத்தை ஒரு கோட்டைக்கொண்டு போர்த்தும் போது கிடைக்கும் சார்பு போர்த்தும் சார்பு w(t) (Wrapping function) ஆகும். 

(iii) மெய்யெண் t -ஆல் ஆன முக்கோணவியல் சார்பின் மதிப்பு கோண t ஆரையன்களிடத்து முக்கோணவியல் சார்பின் மதிப்பாகும்.

(iv) சீரான இடைவெளியில் இயங்கும் அலைவு மற்றும் அலைகளின் மாதிரி நிகழ்வுகளைப் பற்றி படிப்பதற்கு மெய்யெண்களின் முக்கோணவியல் சார்புகள் பயன்படுகிறது.

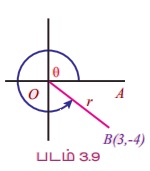
எடுத்துக்காட்டு 3.8 திட்டநிலையில் உள்ள θ -ன் முனையப் பக்கம் (3, -4) என்ற புள்ளி வழியாகச் செல்கிறது எனில் θ -ன் ஆறு முக்கோணவியல் சார்பின் மதிப்புகளைக் காண்க.

தீர்வு:

B (x, y) = B (3, - 4) என்க . 

திட்ட நிலையில் θ கோணத்தின் ஆரம்பப் பக்கம் OA எனவும் முனையப் பக்கம் OB எனவும் கொள்க. ∠AOB = θ மேலும் முனையம் நான்காவது காற்பகுதியில் இருக்கும்.

முக்கோணவியல் சார்புகளின் குறியீடுகள் (Signs of Trigonometric functions)

மையம் ஆதியில் உள்ளவாறு ஓரலகு வட்டத்தை கருதுவோம். திட்டநிலையில் θ - வை கொள்க, கோணம் θ -க்கு ஒத்ததாக P (x, y) ஓரலகு வட்டத்தின்மீது ஏதேனும் ஒரு புள்ளி எனில் cos θ = x, sin θ = y மற்றும் tan θ = y/x ஆகும். P-எக் காற்பகுதியில் இருக்கிறதோ அதைப்பொறுத்து x மற்றும் y-ன் மதிப்புகள் மிகை அல்லது குறையாக இருக்கும்.

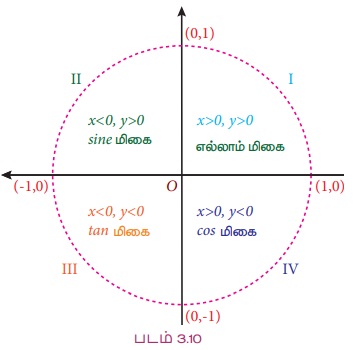
முதல் காற்பகுதியில்

cos θ = x > 0 (மிகை ) 

sin θ = y > 0 (மிகை )

எனவே, sin θ, cos θ மற்றும் அனைத்து முக்கோணவியல் சார்புகளும் முதல் காற்பகுதியில் மிகை மதிப்புடையவை. 

இரண்டாம் காற்பகுதியில்

cos θ = x < 0 (குறை )

sin θ = y > 0 (மிகை ) 

இவ்வாறாக sin θ மற்றும் cosec θ ஆகியவை மிகை மதிப்புடையது மற்றைய சார்புகள் குறை மதிப்புடையது.

இதேபோல் மற்றைய காற்பகுதிகளில் முக்கோணவியல் சார்புகளின் குறியீடுகளை நாம் கண்டறியலாம் என்பதை படம் 3.10 இல் காணலாம். 

குறிப்பு: வெவ்வேறு காற்பகுதியில் முக்கோணவியல் சார்புகளின் குறியீடுகளை கீழ்க்கண்டவாறு நினைவில் கொள்ளலாம்

எடுத்துக்காட்டு 3.9 sin θ = 3/5 மற்றும் θ இரண்டாம் காற்பகுதியில் அமைந்தால் மற்ற ஐந்து முக்கோணவியல் சார்புகளைக் காண்க.

தீர்வு:

sin2 θ + cos2 θ = 1 

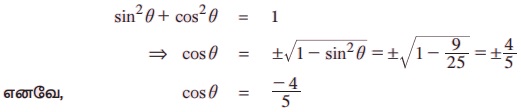
ஏனெனில், இரண்டாம் காற்பகுதியில் cos θ ஒரு குறை மதிப்புடையது.

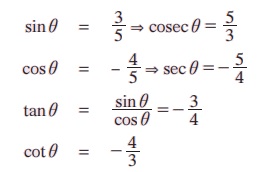
குறிப்பு: sin θ மற்றும் cos θ ஆகியவை தெரியும் எனில், தலைகீழ் முற்றொருமை மற்றும் வகுத்தல் முற்றொருமைகளை பயன்படுத்தி மற்றைய நான்கு சார்புகளின் முக்கோணவியல் மதிப்புகளைக் காணலாம். ஒரு முக்கோணவியல் சார்பின் மதிப்பும் மற்றும் கோணம் அமையும் காற்பகுதியும் தெரிந்தால் பித்தாகரஸ் முற்றொருமையைப் பயன்படுத்தி மற்றைய சார்புகளின் முக்கோணவியல் மதிப்புகளைக் காணலாம்.

3. தொடர்புடைய கோணங்கள் (Allied Angles)

இரண்டு கோணங்களின் கூடுதல் அல்லது வித்தியாசம் - ஆரையன்கள் மடங்காக இருப்பின் அவை தொடர்புடைய கோணங்கள் எனப்படும். 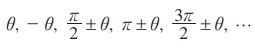ஆகியவற்றில் எந்த இரு θ கோணங்களும் தொடர்புடைய கோணங்களாகும்.

θ மற்றும் - θ ஆகிய தொடர்புடைய கோணங்களைக் கொண்ட முக்கோணவியல் விகிதங்களைக் காண்போம்.

θ வின் வாயிலாக (-θ) இன் முக்கோணவியல் விகிதங்கள் (Trigonometric ratio of (-θ) in terms of θ)

∠AOL = θ மற்றும் ∠AOM = – θ என்க. OL மீது உள்ளபுள்ளி P (a, b) என்க.

OP = OP' என்றமையும்படி OM மீது P' எடுத்துக்கொள்க. 

OA-க்கு செங்குத்தாக PN-ஐ வரையவும் அது OM ஐ P'-ல் சந்திக்கட்டும். 

∠AOP = ∠AOP' மற்றும் ∠PON = ∠P'ON

∆PON மற்றும் ∆P'ON ஆகியவை சர்வசமமுடையதாகும்.

எனவே, PN = P’N மற்றும் P'-ன் கூறுகள் P' (a, - b) என ஆகும்.    

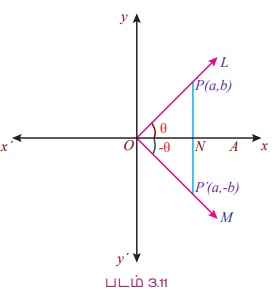
முக்கோணவியல் சார்புகளின் வரையறைப்படி

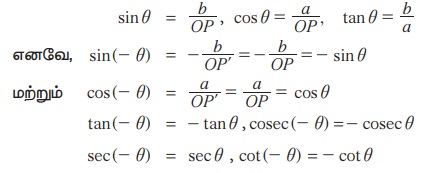
ஆகியவற்றை எளிதில் பெறலாம்.

குறிப்பு: (i) x-அச்சைப் பொறுத்து ஓரலகு வட்டமானது சமச்சீர் என்பதிலிருந்துsin(-θ) = - sin θ மற்றும் cos (-θ) = cos θ என்ப தைப் பெறலாம். θ ஐப் போன்றே - θ இருப்பினும் அது x அச்சின் மற்றொரு பக்கத்தில் அமைந்துள்ளது. சமச்சீர் முறையில் புள்ளி (x, y) ஐ x அச்சைப் பொருத்து பிரதிபலிக்கும்போது (x, - y) கிடைக்கிறது. இங்கு y அச்சுத் தூரம் ஒரு குறை எண்ணாகிறது என்பதால் சைன் ஒரு குறை எண்ணாகும். ஆனால் x அச்சுத் தூரத்தில் மாற்றம் இல்லை என்பதால் கொசைனில் மாற்றம் இல்லை. 

(ii) குறை கோண முற்றொருமைகளைப் பயன்படுத்தி முக்கோணவியல் சார்புகள் ஒற்றைச் சார்புகளா அல்லது இரட்டைச் சார்புகளா என்பதை தீர்மானிக்கலாம்.

எடுத்துக்காட்டு 3.10 மதிப்பைக் காண்க : (i) sin (- 45°) (ii) cos (- 45°) (iii) cot (- 45°)

தீர்வு:

(i) sin (- 45°) = - sin (45°) = -1/√2

(ii) cos (- 45°) =1/√2

(iii) cot (- 45°) = -1

முந்தைய வகுப்பில் (90° - θ), (0 < θ < π/2) என்ற கோணத்தின் முக்கோணவியல் விகிதங்களை பற்றி அறிந்துள்ளோம். இவ்வாறான முக்கோணவியல் விகிதங்களை கீழ்க்கண்டவாறு காணலாம்.

sin(90° - θ) = cosθ,            cos(90° - θ) = sinθ

tan(90° - θ) = cot θ,           cosec(90° - θ) = secθ

sec(90° - θ) = cosecθ,          cot(90° - θ) = tanθ 

மேற்கண்டுள்ள முக்கோணவியல் விகிதங்களுக்கு, (90° + θ) என்ற கோணத்திற்கு தற்போது வரையறுப்போம்.

(90° + θ), (0 < θ < π/2) அமைப்பிலுள்ள கோணங்களின் முக்கோணவியல் விகிதங்கள் (Trigonometric ratios of an angle of the form  (90° + θ), (0 < θ < π/2)in terms of θ).

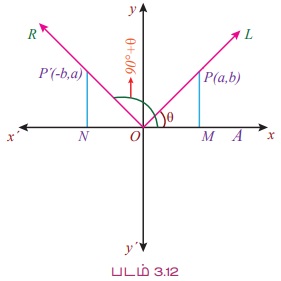
∠AOL = θ மற்றும் ∠AOR = (90° + θ) என்க. இங்கு P (a, b) என்பது OL மீது இருக்கும் ஒரு புள்ளி மற்றும் P' என்னும் ஒரு புள்ளியானது, OP = OP' ஆக இருக்கும்படி OR - இன் மீது தேர்வு செய்க

Ox மற்றும் Ox' மீது P மற்றும் P' இலிருந்து, PM மற்றும் P'N ஆகிய செங்குத்துக் கோடுகளை வரைக.

இங்கு , ∠AOP' = 90° + θ

தெளிவாக, ∆OPM மற்றும் ∆P'ON ஆகியவை சர்வசமமுடையதாகும்.

ON = MP மற்றும் NP' = OM.

எனவே, P மற்றும் P' இன் ஆயத் தொலைகள் முறையே P (a, b) மற்றும் P' (- b, a) ஆகும்.

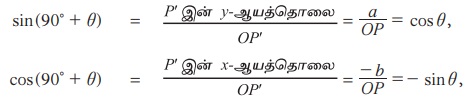
எனவே,     tan(90° + θ)=- cot θ, cosec (90° + θ) = sec θ,

sec(90° + θ)=- cosec θ, cot(90° + θ) = - tan θ

π± θ, 3π/2 ± θ, 2π± θ ஆகிய தொடர்புடைய கோணங்களின் முக்கோணவியல் சார்புகளை இதே முறையில் கண்டறியலாம்.

மேற்கண்ட முடிவுகள் பின்வரும் அட்டவணையில் தொகுக்கப்பட்டுள்ளது. இங்கு (0 < θ < π /2).

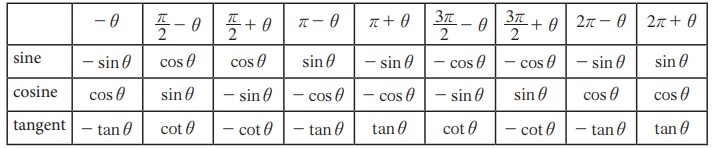
குறிப்பு: (i) மேற்கண்ட அட்டவணையிலிருந்து ஒத்த தலைகீழ்விகிதங்களை எழுதலாம்.

(ii) 2n π/2 ± θ, n ∈ Z என்ற அமைப்பிலுள்ள தொடர்புடைய கோணங்கள் அதாவது ± θ, π ± θ, 2π ± θ ஆகியவைகளுக்கு முக்கோணவியல் விகிதம் மாறாது. (சைன் மாறாமல் சைன் ஆகவும், கொசைன் மாறாமல் கொசைன் இருக்கும்,)

(iii) (2n + 1) π/2 ± θ, n ∈ Z என்ற அமைப்பில் உள்ள தொடர்புடைய கோணங்கள் அதாவது π/2± θ,3π/2 ± θ ஆகியவைகளுக்கு முக்கோணவியல் விகிதங்கள் அவற்றின் நிரப்பி விகிதங்களாக மாறும். 'co' இல்லாதவைகளுக்கு சேர்த்தும் அது இருப்பின் அதை விலக்கியும் எழுத வேண்டும் (சைனை கொசைனாகவும், கொசைனை சைனாகவும் மாற்ற வேண்டும்). 

(iv) விகிதத்தின் குறியீடுகளைக் கண்டறியக் கோணம் அமையும் காற்பகுதிகளை முதலில் கண்டறிய வேண்டும். பின்பு காற்பகுதி விதியான “ASTC” விதியின்படி குறியீடுகளை ( + அல்லது - ஐ) இணைக்க வேண்டும்.

எடுத்துக்காட்டு 3.11 மதிப்புகளைக் காண்க (i) sin 150° (ii) cos 135° (iii) tan 120° .

தீர்வு:

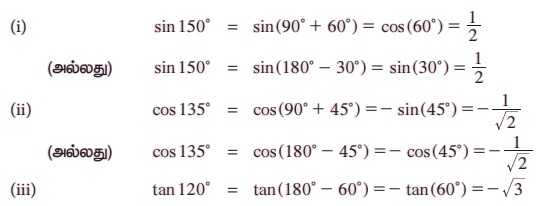
(அல்லது) tan 120° ஐ tan (90° + 30°) என எழுதி மதிப்பைக் காண்க.

எடுத்துக்காட்டு 3.12 மதிப்பு காண்க (i) sin (765°) (ii) cosec (- 1410°) (iii) cot (- 15π/4).

தீர்வு:

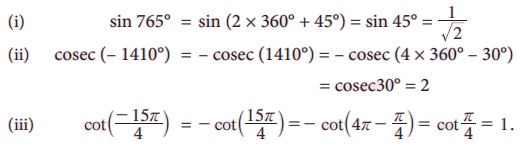
எடுத்துக்காட்டு 3.13 நிறுவுக tan (315°) cot (- 405°) + cot (495°) tan (- 585°) = 2.

தீர்வு:

இடப்பக்கம் = tan (360° - 45°) [- cot (360° + 45°)] + cot (360° + 135°) [-tan (360° 225°)] 

= [- tan 45°] [- cot 45°] + [- tan 45°) [- tan 45°] 

= (- 1) (- 1) + (- 1) (- 1) = 2.

4. முக்கோணவியல் சார்புகளின் சில குணாதிசயங்கள் (Some characteristics of Trigonometricfunctions)

முக்கோணவியல் சார்புகள் சில அருமையான குணாதிசயங்களைப் பெற்றிருக்கின்றன. எடுத்துக்காட்டாக,

(i) சைன் மற்றும் கொசைன் சார்புகள் ஒன்றுக்கொன்று நிரப்பிகள் ஆகும். அதாவது sin(90° - θ) = cos θ மற்றும் cos(90° - θ) = sin θ. 

(ii) ஓரலகு வட்டத்தின் மீதுள்ள ஒரு புள்ளியின் கூறுகளாக cosθ மற்றும் sinθ ஆகியவைபெறப்படுகின்றன, அவை - 1≤ cosθ ≤ 1 மற்றும் -    1≤ sinθ ≤ 1 என்ற சமனிலியை பூர்த்தி செய்கின்றன. எனவே, cosθ, sinθ ∈    [- 1,1]. 

(iii) ஒரு சீரான இடைவெளியில் முக்கோணவியல் சார்புகள் அதன் மதிப்பை மீண்டும் மீண்டும் பெறுகின்றது. 

(iv) சைன் மற்றும் கொசைன் சார்புகள் cos (-θ) = cos θ மற்றும் sin(-θ) = - sin θ என்ற வியக்கத்தக்க பண்புகளை பெற்றிருக்கும்.  இறுதியில் உள்ள இரு பண்புகளை ஆராய்வோம்.

முக்கோணவியல் சார்புகளின் காலமுறைப் பண்புகள் (Periodicity of Trigonometric functions)

ஒரு சிறிய மிகை p-க்கு, சார்பு f ஆனது சார்பகத்தில் உள்ள அனைத்து x-ற்கும், f (x + p) = f (x) என்றவாறு இருந்தால் அச்சார்பு p காலம் உடைய திரும்பு அல்லது காலவட்டச் சார்பு என்பது நமக்கு தெரியும்.

எடுத்துக்காட்டாக,

sin(x + 2nπ) = sinx, n ∈ Z என்பது நமக்குத் தெரியும், 

அதாவது  sin (x + 2 π) = sin (x + 4 π) = sin(x + 6 π) = ... = sinx. 

எனவே sinx 2π காலம் கொண்ட காலவட்டச் சார்பு 2 π ஆகும். 

இதேபோல் 2π காலம் கொண்ட காலவட்டச் சார்புகள் cosx, cosecx மற்றும் secx ஆகும். 

ஆனால் π காலம் கொண்ட காலவட்டச் சார்புகள் tanx மற்றும் cotx ஆகும்.

sinx மற்றும் cosx ஆகியவற்றின் காலமுறைப் பண்பை அதன் வரைபடங்களைக் கொண்டு எளிதில் காணலாம்.

(i) சைன் சார்பின் வரைபடம்

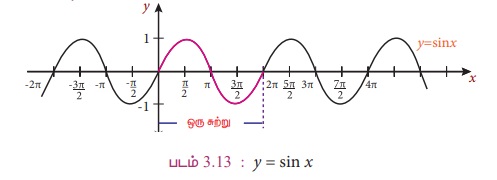
கோணத்தைக் குறிக்கும் மாறியை x என்க. கிடைமட்ட அச்சை x- அச்சாகவும், நேர்குத்து அச்சை y-அச்சாகவும் கொள்க. y = sinx என்ற சார்பின் வரைபடம் படம் 3.13 ஆகும். முதலாவதாக, 2 π இடைவெளி கொண்ட காலமுறைச் சீரமைப்பைக் காணலாம். வடிவகணித ரீதியில் இதன் பொருள் என்னவென்றால் படத்திலுள்ள வளைவரையை 2 π அளவு இடப்பக்கமாகவோ அல்லது வலப்பக்கமாகவோ நகர்த்தினால் மீண்டும் அதே வளைவரை மீது சரியாகப் பொருந்தும். இரண்டாவதாக, வரைபடம் y அச்சில் ஓரலகிற்குள் மட்டும் இருப்பதைக் கவனிக்கவும். வரைபடம் சீர் இடைவெளியில் கூடும் மற்றும் குறையும் சார்பாக உள்ளது. அதாவது - π/2லிருந்து π/2 வரை கூடும் சார்பாகவும், π/2 லிருந்து 3π/2 வரை குறையும் சார்பாகவும் உள்ளது.

(ii) கொசைன் சார்பின் வரைபடம்

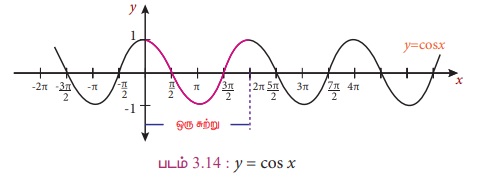
வரைபடம் y = cos x ஆனது y = sin x வரைபடத்தைப் போன்றுள்ளது என்பதைக் கவனிக்கலாம். சைன் சார்பின் வரைபடத்தை இடப்புறமாக π/2 அளவு நகர்த்தும்போது கொசைன் சார்பின் வரைபடம் கிடைக்கிறது. இதற்குக் காரணம் cosx = sin(π/2+x) என்ற முற்றொருமை ஆகும். cosx = cos(- x) = sin(π /2+x) என்பதை வரைபடத்தில் எளிதாகக் காணலாம்.

குறிப்பு: (i) சைன் மற்றும் கொசைன் சார்புகள் காலமுறை பண்பைப் பெற்றிருப்பதால் அவைகள் பெரிதும் பயன்படக் காரணமாகிறது. நம்மைச் சுற்றி நடக்கும் பல நிகழ்வுகள் காலமுறை பண்புடையவை. எடுத்துக்காட்டாக, சூரிய உதயம் மற்றும் மறைதல், சுருளின் (Spring) மேல் மற்றும் கீழ்நோக்கி இயக்கம், கடல் அலைகள் ஆகியவை சம இடைவெளியில் (நேரத்தில்) மீண்டும் மீண்டும் நிகழ்தல், அனைத்துக் காலமுறை நிகழ்வுகளையும் சைன் மற்றும் கொசைன் சார்புகளை இணைத்துப் புரிந்துகொள்ள முடியும். 

(ii) அறிவியல் முழுவதும் சீரான இடைவெளியில் நடக்கும் அலைவுகள், அலைகள் மற்றும் பிற இயல்பான நிகழ்வுகளுக்குக் காலமுறைச் சார்புகள் பயன்படுத்தப்படுகின்றன.

ஒற்றை மற்றும் இரட்டை முக்கோணவியல் சார்புகள் (Odd and even trigonometric functions)

ஒற்றை மற்றும் இரட்டைச் சார்புகள் சில சமச்சீர் பண்புகளை நிறைவுப்படுத்துகிறது. x இன் எல்லா மெய்யெண் மதிப்பிற்கும் f(- x) = f (x) எனில், f (x) ஓர் இரட்டைச் சார்பு மேலும் xஇன் எல்லா மதிப்பிற்கும் f(x) =- f (x) எனில் f (x) ஓர் ஒற்றைச் சார்பு. பல்லுறுப்புக் கோவை அல்லாத இரட்டை மற்றும் ஒற்றைச் சார்புகளுக்கு முக்கோணவியல் சார்புகள் ஒரு சிறந்த எடுத்துக்காட்டாகும்.

x இன் எல்லா மதிப்பிற்கும் cos (- x) = cos x எனவே cos x ஓர் இரட்டைச் சார்பு ஆகும். 

x இன் எல்லா மதிப்பிற்கும் sin (- x) = - sin x எனவே sin (x) ஓர் ஒற்றைச் சார்பு ஆகும்.

அதேபோல் sec x ஓர் இரட்டைச் சார்பு ஆகும். அதேபோல் tan x, cosec x மற்றும் cot x ஆகியவை ஒற்றைச் சார்புகளாகும். f(t) = t - cost என்பது இரட்டைச் சார்பும் அல்ல, ஒற்றைச் சார்பும் அல்ல (ஏன்?)

எடுத்துக்காட்டு 3.14 பின்வரும் சார்புகளை ஒற்றைச்சார்பு, இரட்டைச்சார்பு மற்றும் இரண்டும் இல்லை என வகைப்படுத்துக.

(i) sin2 x - 2 cos2 x - cos x (ii) sin (cos (x)) (iii) cos (sin (x)) (iv) sin x + cos x 

தீர்வு:

(i)  f (x) = sin2 x - 2 cos2 x - cos x என்க,

f (- x) = f (x) [ ஏனெனில், sin (- x) = - sin x மற்றும் cos (-x) = cos x] 

எனவே, f (x) ஓர் இரட்டைச் சார்பு. 

(ii) f (x) = sin (cos (x)) என்க, 

f(- x) = f (x), f (x) ஓர் இரட்டைச் சார்பு. 

(iii) f (x) = cos (sin (x)), f (- x) = f (x), எனவே, f (x) ஓர் இரட்டைச் சார்பு.

(iv) f (x) = sin x + cos x

f (- x) ≠ f (x) மற்றும் f (- x) ≠ - f (x) 

எனவே, f (x) = sin x + cos x என்பது இரட்டைச் சார்பும் அல்ல, ஒற்றைச் சார்பும் அல்ல.

குறிப்பு: (i) பொதுவாக ஒரு சார்பின் வரைபடத்தில் y-அச்சை பிரதிப்பலிப்பதில் மாறாமல் இருந்தால் அச்சார்பு இரட்டைச்சார்பாகும். ஆதியைப் பொறுத்து மாறாமல் வரைபடம் சமச்சீராக இருந்தால் அது ஒற்றைப்படை சார்பாகும். 

(ii) முக்கோணவியல் சார்புகளைப் பகுப்பாய்வு செய்வதற்குக் குறிப்பாகக் கூட்டல் மற்றும் கழித்தல் சூத்திரத்தில், ஒற்றை மற்றும் இரட்டைச் சார்புகளின் பண்புகள் பயனுள்ளதாக இருக்கும். 

(iii) சில வரையறுக்கப்பட்ட தொகையிடலை மதிப்பீடு செய்வதற்கு இரட்டை மற்றும் ஒற்றைச் சார்புகளின் பண்புகள் பயனுள்ளதாக இருக்கும். இதை நாம் நுண்கணிதத்தில் பார்ப்போம்.

பயிற்சி 3.3

1. மதிப்புக்களைக் காண்க.

(i) sin (480°) 

(ii) sin (- 1110°) 

(iii) cos (300°) 

(iv) tan (1050°)

(v) cot (660°)

(vi) tan(19π/3)

(vii) sin( -11π/3 ) 

2. திட்டநிலையில் உள்ள θ-ன் முனையப் பக்கம் (5/7, 2√6/7 என்ற புள்ளி செல்கிறது எனில் θ-ன் ஆறு முக்கோணவியல் சார்பின் மதிப்புகளைக் காண்க.

3. பின்வரும் சார்பின் மதிப்பிற்கு மற்ற ஐந்து முக்கோணவியல் சார்புகளைக் காண்க.

(i) cosθ = -1/2,   θ மூன்றாம் காற்பகுதியில் உள்ளது.

(ii) cos θ = 2/3,  θ முதல் காற்பகுதியில் உள்ளது.  

(iii) sin θ = -2 ,   θ நான்காம் காற்பகுதியில் உள்ளது.

(iv) tan θ = - 2 ,  θ இரண்டாம் காற்பகுதியில் உள்ளது.

(v) sec θ = 13/5,   θ நான்காம் காற்பகுதியில் உள்ளது.

4. நிருபிக்க : 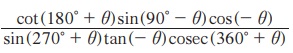= cos2 θ cot θ. 

5. sin2 θ = 3/4 என்ற சமன்பாட்டை நிறைவு செய்யும் 0° இக்கும் 360° இக்கும் இடைப்பட்ட அனைத்துக் கோணங்களைக் காண்க.

6. 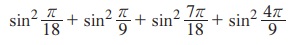= 2 எனக் காண்பி .