முக்கோணவியல் சமன்பாடுகள்

முக்கோணவியல் சமன்பாடுகள் (Trigonometric Equations)

அறியப்படாத கோணங்களினாலான, முக்கோணவியல் சார்புகளை உள்ளடக்கிய சமன்பாட்டை முக்கோணவியல் சமன்பாடுகள் என்று அழைக்கலாம். அறியப்படாத கோணங்களின் மதிப்பு, சமன்பாட்டைப் பூர்த்தி செய்தால் அதுவே முக்கோணவியல் சமன்பாட்டின் தீர்வு ஆகும்.

சார்பகத்தை கட்டுபடுத்தவில்லை என்றால், முக்கோணவியல் சார்பின் கால வட்ட பண்பின் காரணத்தால் முக்கோணவியல் சமன்பாட்டிற்கு எண்ணற்ற தீர்வுகள் இருக்கும். சில சமன்பாடுகளுக்குத் தீர்வு இல்லாமல் இருக்கும்.

எடுத்துக்காட்டாக, sinθ = 3/2 என்ற சமன்பாட்டிற்கு தீர்வு இல்லை காரணம்  - 1 ≤ sinθ ≤ 1. 

sinθ = 0 என்ற சமன்பாட்டிற்கு எண்ண ற்ற பல தீர்வுகள் உள்ளன அதாவது θ = ±π ± 2π, ± 3π,.. இவ்வாறு முக்கோணவியல் சமன்பாட்டின் தீர்வு எண்ணற்றவை மற்றும் அத்தீர்வுகள் கால வட்டங்களில் காணப்படும்.

பொதுத் தீர்வு (General Solution)

ஒரு முக்கோணவியல் சார்பின் காலவட்டத்தின் உதவியுடன் பெறப்படும் ஒரு முக்கோணவியல் சமன் பாட்டின் அனைத்து மதிப்புகள் அச்சமன்பாட்டின் பொதுத் தீர்வு என்று அழைக்கப்படும்.

முதன்மைத் தீர்வு (Principal Solution)

[0,2π] அல்லது [-π, π] இடைவெளிகளில் சமன்பாட்டைப் பூர்த்தி செய்யும் அறியப்படாத கோணத்தின் எண்ணளவில் சிறிய எண் மதிப்பை முதன்மை தீர்வு என்று அழைக்கலாம். இங்கு நாம் முதன்மை தீர்வு வரையறுக்க     [-π, π) என்ற இடைவெளியை எடுத்துக் கொள்வோம். மேலும் இந்த இடைவெளியில் இரண்டு தீர்வுகள் இருக்கலாம். இரண்டு தீர்வுகள் சரியாக இருந்தாலும் நாம் எண்ணளவில் மிகச்சிறியதை எடுத்துக்கொள்வோம். இது நமக்கு முக்கோணவியல் சார்புகளுக்கு ஒத்த முதன்மை சார்பகத்தை வரையறுக்க உதவுகிறது.

[-π / 2, π / 2] என்ற இடைவெளியில் சைன் சார்பின் முதன்மை மதிப்பு இருக்கிறது. அதாவது முதல் அல்லது நான்காம் காற்பகுதியில் இருக்கிறது.

[0, π] என்ற இடைவெளியில் கொசைன் சார்பின் முதன்மை மதிப்பு இருக்கிறது. அதாவது முதல் அல்லது இரண்டாம் காற்பகுதியில் இருக்கிறது.

(-π/2, π/2) என்ற இடைவெளியில் தொடுசார்பின் முதன்மை மதிப்பு இருக்கிறது. அதாவது முதல் அல்லது நான்காம் காற்பகுதியில் இருக்கிறது.

குறிப்பு: (i) முக்கோணவியல் சமன்பாடுகள் முக்கோணவியல் முற்றொருமையிலிருந்து வேறுபடுகின்றன. ஏனென்றால் கோணம் θ-வின் அனுமதிக்கப்பட்ட அனைத்து மதிப்புகளுக்கு முக்கோணவியல் முற்றொருமைகள் உண்மையாகும். ஆனால் அறியப்படாத சில குறிப்பிட்ட கோணங்களுக்கு மட்டும் முக்கோணவியல் சமன்பாடுகள் செல்லுபடியாகும்.

(ii) முக்கோணவியல் சமன்பாடுகளுக்குத் தீர்வுகாணப் பொதுவான முறை ஏதும் இல்லை. ஆனாலும் சில சமன்பாடுகளைக் காரணிப்படுத்தியும்; சில சமன்பாடுகளைத் தனித் தனிச் சார்புகளாக மாற்றியும்; சில சார்புகளை வர்க்கப்படுத்தியும் தீர்வு காணலாம் என்பதைக் கவனிக்கவும்.

(iii) முக்கோணவியல் சமன்பாடுகளைச் சில நேரங்களில் இருபுறமும் வர்க்கப்படுத்தும் யுக்தியைப் பயன்படுத்தலாம். அச்சமயத்தில் தவறான தீர்வுகளும் கிடைக்க வாய்ப்புள்ளது (வெளிப்புறத் தீர்வு - Extraneous solution). எடுத்துக்காட்டாக, 0 ≤ x < 360° எனும் போது sinx - cosx = 1 என்ற சமன்பாட்டின் தீர்வுகாண இருபுறமும் வர்க்கப்படுத்தக் கிடைப்பது (sinx - 1)2 - = cos2 x ⇒ 2 sinx(sinx - 1) = 0 அதாவது x = 0, π /2+, π என்ற தீர்வு கிடைக்கிறது. ஆகவே, x = 0 ஒரு தவறான தீர்வு. எனவே, வர்க்கப்படுத்தும் முறையில் சரியான தீர்வு காணச் சரிபார்த்தல் செய்தல் வேண்டும்.

(iv) முக்கோணவியல் சமன்பாடுகளின் தீர்வுகளை எழுதும்போது ஆரையன் அளவுஅதிகம் பயன்படுத்தப்படுகிறது. இப்போது நாம் வெவ்வேறு வடிவில் உள்ள முக்கோணவியல் சமன்பாடுகளின் தீர்வை காண்போம்.

(i) sin θ = k(- 1<k < 1) என்ற அமைப்பிலுள்ள சமன்பாட்டின் தீர்வு :

sin α = k என்றவாறு எண்ணளவில் சிறிய கோணம் α என எடுத்துக்கொள்வோம்.

எனவே, sinθ = sinα 

sin θ – sin α = 0

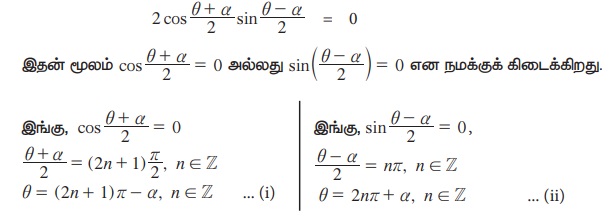
(i) மற்றும் (ii)-லிருந்து நமக்குக் கிடைப்பது.

sin θ =sin α     ⇒ θ = n π + (- 1)n a, n∈ Z                                                       (3.13)

(ii) cos θ = k (- 1≤ k ≤ 1) என்ற அமைப்பிலுள்ள சமன்பாட்டின் தீர்வு : 

cos a = k என்றவாறு எண்ணளவில் சிறிய கோணம் α என எடுத்துக்கொள்வோம்.

இவ்வாறாக,

cos θ = cos α 

cos θ - cos α = 0 

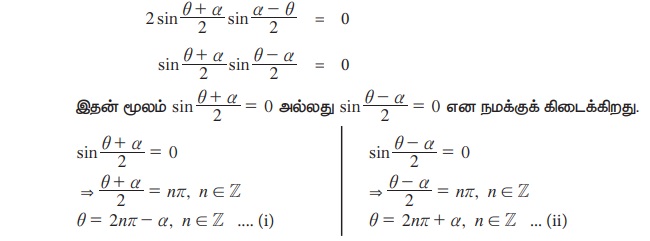
(i) மற்றும் (ii)-லிருந்து நமக்கு கிடைப்பது.

cos θ = cos α       θ = 2n π ± a, n ∈ Z           (3.14)

(iii) tan θ = k (-∞ < k < ∞) என்ற அமைப்பிலுள்ள சமன்பாட்டின் தீர்வு: 

tan α = k என்றவாறு Q எண்ண ளவில் சிறிய கோணம் என எடுத்துக்கொள்வோம்.

tan θ = tan α 

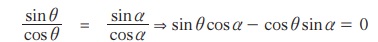
sin (θ – α ) = 0 ⇒ θ – α = n π

θ = n π + α, n ∈ Z

எனவே,

tan θ = tan α       θ = n π + α , n ∈ Z                                            (3.15)

(iv) a cos θ + b sin θ = c என்ற அமைப்பிலுள்ள சமன்பாட்டின் தீர்வு : 

a = rcos α, b = rsin α என எடுத்துக்கொள்வோம்.

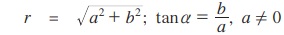
acos θ + bsin θ = c = rcos α cos θ + rsin α sin θ = c

rcos (θ – α) = c

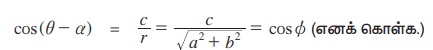
θ - α = 2n π ± ϕ, n ∈ Z

θ = 2n π + a ± ϕ , n ∈ Z

குறிப்பு: 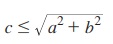எனும் போது மட்டுமே மேலே குறிப்பிட்ட முறையைப் பயன்படுத்தலாம். 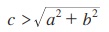எனில், acos θ + b sin θ = c என்ற சமன்பாட்டிற்கு எந்த தீர்வும் இல்லை.

நாம் இப்போது முக்கோணவியலின் சமன்பாடுகளின் பொதுத் தீர்வை சுருக்கமாகக் கூறுவோம்.

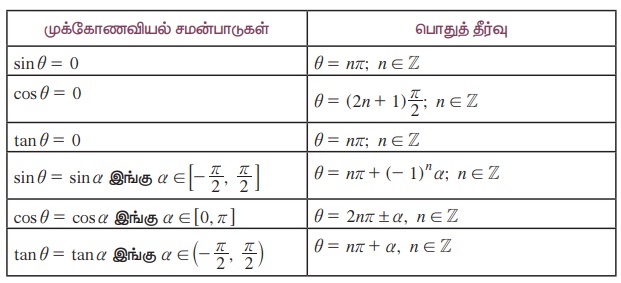
எடுத்துக்காட்டு 3.42 முதன்மை தீர்வை காண்க 

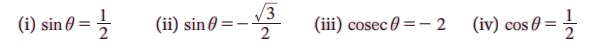
தீர்வு: 

எடுத்துக்காட்டு 3.43 sin θ = -√3/2 - ன் பொதுத் தீர்வை காண்க.

தீர்வு:

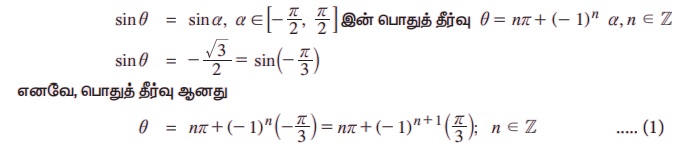
குறிப்பு: மேலே கிடைக்கப் பெற்ற பொதுத் தீர்வில் -(π/3)-ஐ முதன்மை மதிப்பாக எடுக்கிறோம் அது வழக்கமாக (-π, π) என்ற இடைவெளியில் எண்ண ளவில் சிறியதை முதன்மை மதிப்பு என்கிறோம். இந்த எடுத்துகாட்டின் மூலம் முதன்மை தீர்வு வரையறையில் குறிப்பிட்டதுபோல் [0, 2π] என்ற இடைவெளியிலும் முதன்மை மதிப்பை எடுக்கலாம் என்பதை நியாயப்படுத்தலாம். 

[0, 2π] என்ற இடைவெளியில் முதன்மை தீர்வு எடுத்துக்கொண்டால், பிறகு முதன்மை தீர்வு θ = 4 π/3 மற்றும் பொதுத்தீர்வு 

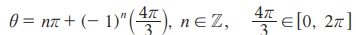... (ii) என்றாகிறது 

(ii)-இல் n = 0, - 1, 1, - 2, 2,... எனக் கொண்டால் அதற்கொத்த தீர்வுகள் 

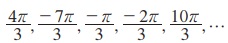ஆகும்.

(i) -இல் n = 0, - 1, 1, - 2, 2, … எனக் கொண்டால் அதற்கொத்த தீர்வுகள்

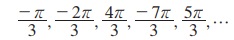ஆகும் 

இரண்டு வழிகளிலும் நமக்கு ஒரே தீர்வுகள் கிடைக்கின்றன, ஆனால் வெவ்வேறு வரிசை கொண்டவை. இந்த விவாதத்திலிருந்து [0, 2π) அல்லது [-π, π) என்ற இடைவெளியில் எண்ணளவில் சிறியதை முதன்மை தீர்வாக எடுக்கலாம் என்பது நியாயப்படுத்தப்படுகிறது.

எடுத்துக்காட்டு 3.44 பொதுத் தீர்வை காண்க . (i) sec θ =-2 (ii) tan θ = √3

தீர்வு:

(i)  sec θ =- 2

 sec θ = - 2 = cos θ = -1/2 

 cos θ = cos α, α ∈ [0, π] இன் பொதுத் தீர்வு

 θ = 2nr ± α, n ∈ Z என நமக்குத் தெரியும். 

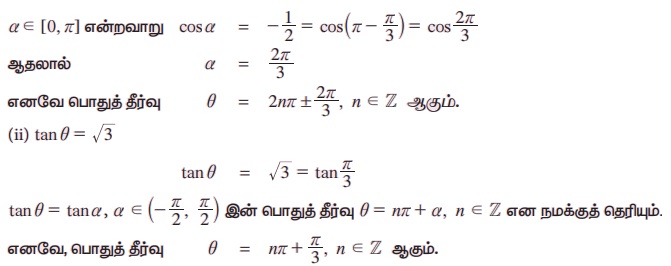
எடுத்துக்காட்டு 3.45 தீர்க்க 3 cos2 θ = sin2θ. 

தீர்வு:

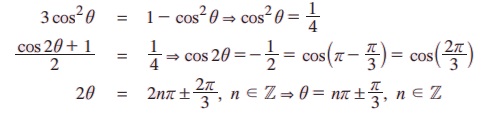
குறிப்பு: tan2 θ = 3 என எழுதித் தீர்வுகாண முயற்சி செய்க.

எடுத்துக்காட்டு 3.46 தீர்வு காண் sinx + sin 5x = sin 3x.

தீர்வு:

sinx + sin 5x = sin 3x = 2 sin 3x cos 2x = sin 3x 

sin 3x(2 cos 2x – 1) = 0

எனவே, sin 3x = 0 அல்லது cos 2x =1/2

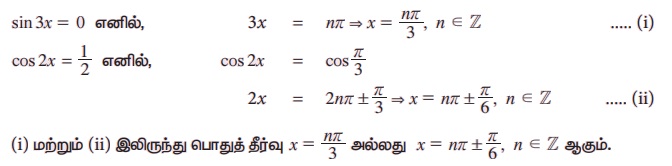
எடுத்துக்காட்டு 3.47 தீர்வு காண்க cosx + sinx = cos 2x + sin 2x. 

தீர்வு:

cos x + sin x = cos 2x + sin 2x

cos x - cos 2x = sin 2x - sin x 

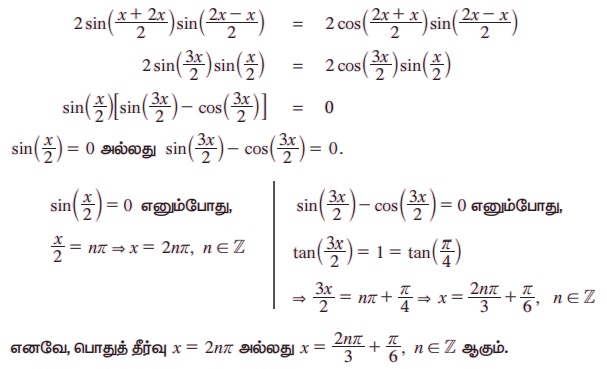
குறிப்பு: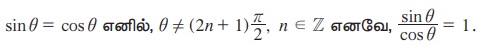

எடுத்துக்காட்டு 3.48 sin 9 θ = sin θ என்ற சமன்பாட்டைத் தீர்க்க.

தீர்வு:

 sin9θ  = sinθ = sin9θ – sinθ = 0

 2cos 5θ sin 4θ = 0 ⇒ cos 5θ = 0 அல்லது sin 4θ = 0

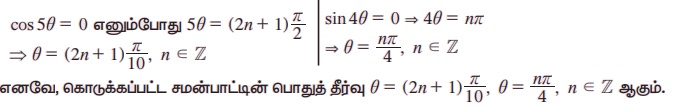
எடுத்துக்காட்டு 3.49 தீர்க்க tan 2x = - cot(x + π/3).

தீர்வு:

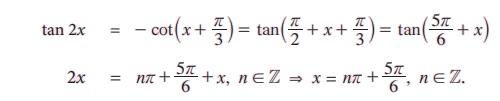
எடுத்துக்காட்டு 3.50 தீர்க்க sin x – 3 sin 2x + sin 3x = COS x - 3 cos 2x + cos 3x.

தீர்வு:

 sin x – 3 sin 2x + sin 3x= cos x – 3 cos 2x + cos 3x

  sin 3x + sin x - 3 sin 2x = cos 3x + cos x – 3 cos 2x

  2 sin 2x cos x - 3 sin 2x = 2 cos 2x cos x - 3 cos 2x 

 (sin 2x - cos 2x) (2cos x - 3) = 0 

எனவே , sin 2x - cos 2x = 0 ஏனெனில், 2 cos x - 3 ≠ 0

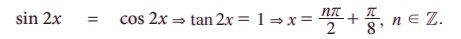
எடுத்துக்காட்டு 3.51 தீர்க்க sin x + cos x = 1 + sin x cos x.

தீர்வு:

sin x + cos x = t என்க

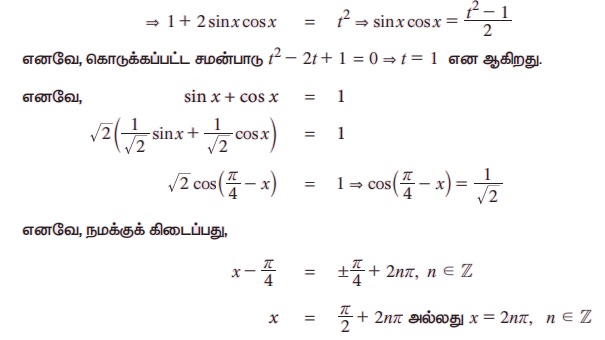
எடுத்துக்காட்டு 3.52 தீர்க்க 2 sin2 x+ sin2x = 2.

தீர்வு:

2 sin2x+ sin22x = 2 = 2 sin2 x + (2 sin x cos x)2 = 2

cos2 x(2 sin2 x – 1) = 0 

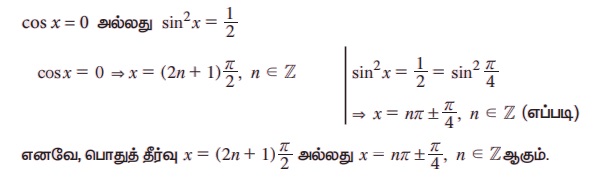
எடுத்துக்காட்டு 3.53 a மற்றும் b என்ற எந்த ஒரு மதிப்பிற்கும் 

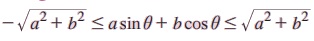என நிறுவுக.

தீர்வு:

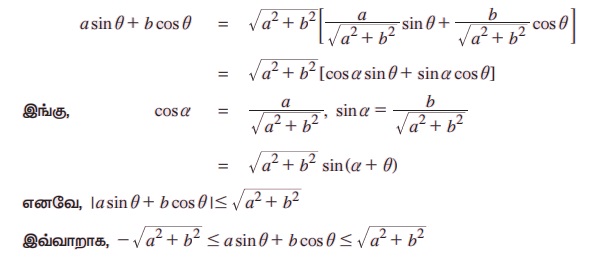
எடுத்துக்காட்டு 3.54 தீர்க்க √3 sinθ – cosθ = √2. 

தீர்வு:

√3 sinθ – cos θ = √2 

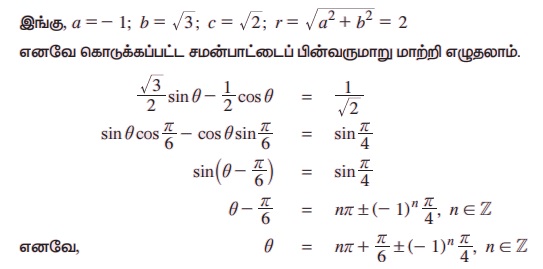
எடுத்துக்காட்டு 3.55 தீர்க்க √3 tanθ + (√3 - 1) tanθ - 1 = 0.

தீர்வு:

√3 tan2θ + (√3 - 1) tan θ - 1 = 0 

√3 tan2 θ+ √3 tanθ – tanθ - 1 = 0

( √3 tan θ – 1)(tan θ + 1) = 0 

எனவே, √3 tan θ - 1 = 0 அல்லது tan θ + 1 = 0

(i) மற்றும் (ii) இலிருந்து நமக்குப் பொதுத் தீர்வு கிடைக்கிறது.

பயிற்சி 3.8

1. பின்வருவனவற்றுக்கு முதன்மை தீர்வு மற்றும் பொதுத் தீர்வுகளைக் காண்க 

(i) sinθ = -1/√2 

(ii) cotθ = √3 

(i) tanθ = -1/√3

2. 0° < θ < 360° என்ற இடைவெளியில் இருக்கும் கீழ்கண்ட சமன்பாடுகளுக்கு சரியானதீர்வுகளைக் காண்க. 

(i) sin4 x = sin2x 

(ii) 2cos2x+ 1 = - 3 cosx 

(iii) 2 sin2 x+ 1 = 3sinx 

(iv) cos 2x = 1 – 3 sinx

3. பின்வரும் சமன்பாடுகளைத் தீர்க்கவும் 

(i) sin 5x - sinx = cos 3x

(ii) 2 cos2 θ + 3sinθ - 3 = 0

(iii) cosθ+ cos 3θ = 2 cos 2θ

(iv) sinθ+ sin3θ + sin 5θ = 0

(v) sin 2θ – cos 2θ – sinθ + cosθ = 0 

(vi) sinθ + cosθ = √2 

(vii) sinθ+ √3cosθ = 1 

(viii) cotθ + cosecθ =√3

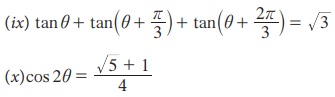
(xi) 2 cos2x- 7 cosx+ 3 = 0