வகைக்கெழுச் சமன்பாடுகளை வகைப்படுத்துதல் (Classification of Differential Equations)

வகைக்கெழுச் சமன்பாடுகளை வகைப்படுத்துதல் (Classification of Differential Equations) 

வரையறை 10.4: (சாதாரண வகைக்கெழுச் சமன்பாடு)

ஒரு வகைக்கெழுச்சமன்பாடு ஒரேயொருசாரா மாறியைப் பொருத்து ஒன்று அல்லது அதற்கு மேற்பட்ட சார்புகளின் சாதாரண வகைக்கெழுக்களைக் கொண்டுள்ளது எனில், அச்சமன்பாடு சாதாரண வகைக்கெழுச் சமன்பாடு எனப்படும்.

வரையறை 10.5: (பகுதி வகைக்கெழுச் சமன்பாடு)

ஒரு வகைக்கெழுச் சமன்பாடு ஒன்று அல்லது அதற்கு மேற்பட்ட சார்புகளின் பகுதி வகைக்கெழுக்களை மட்டும் கொண்டிருக்கும் எனில், அச்சமன்பாடு பகுதி வகைக்கெழுச் சமன்பாடு எனப்படும்.

எடுத்துக்காட்டாக, அறியாத சார்பு y எனவும் சாராமாறி x எனவும் கொள்க. பின்னர் 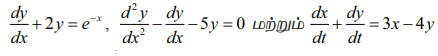என்பவை சாதாரணவகைக்கெழுச்  சமன்பாடுகளுக்கு சில உதாரணங்களாகும்.

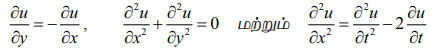என்பவை பகுதி வகைக்கெழுச் சமன்பாடுகளுக்கு சில உதாரணங்களாகும்.

இந்த அத்தியாயத்தில் சாதாரண வகைக்கெழுச் சமன்பாடுகளைப் பற்றி மட்டும் காண்போம்.

சாதாரண வகைக்கெழுச் சமன்பாடுகளை நேரியலான சாதாரண வகைகெழுச் சமன்பாடுகள் மற்றும் நேரியலற்ற சாதாரண வகைக்கெழுச் சமன்பாடுகள் என இரு வேறுபட்ட பிரிவுகளாக வகைப்படுத்தலாம்.

வரையறை 10.6:

வரிசை n உடைய நேரியலான சாதாரண வகைக்கெழுச் சமன்பாட்டின் பொது வடிவம் 

an ( x) y( n) + an−1 ( x) y( n−1) + . . .  + a1 ( x) y' + a0 y = g ( x)         ... (1)

ஆகும். இங்கு, கெழுக்கள் an ( x ) ≠ 0, a0 ( x ) , a1 ( x ), . . . , an−1 (x) மற்றும் g (x) என்பன சாரா மாறி x ஐப் பொருத்த சார்புகளாகும் (பூச்சிய சார்பையும் உள்ளடக்கியது) 

குறிப்பு 

(1) நேரியலான வகைக்கெழுச் சமன்பாடுகளில், ஒரு சார்பு y (x) உடன் அதன் வகைக்கெழுக்கள்பெருக்கலாக இருக்காது. மற்றும் ஒரு சார்பு அல்லது அதன் வகைக்கெழுக்களின் அடுக்கு 1 ஐ விட அதிகமாக இருக்காது என்பது கவனத்தில் கொள்ள வேண்டிய முக்கியமான குறிப்புகளாகும். 

(2) நேரியல் வகைக்கெழுச் சமன்பாடுகளில் yஐப் பொருத்த விஞ்சிய சார்புகள் (முக்கோணவியல், மடக்கை போன்றவை) அல்லது அதனுடைய வகைக்கெழுக்கள் காணப்படாது. 

(3) ஒரு சார்போ அல்லது அதனுடைய வகைக்கெழுக்களோ மற்றொரு சார்பினுள் மாறியாக உள்ளடங்கி இருக்காது. உதாரணமாக, √y' அல்லது ey போன்றவை. 

(4) கெழுக்கள் a0 ( x ) , a1 ( x ), . . . , an−1 ( x ) மற்றும் g(x) ஆகியவை பூச்சிய அல்லது பூச்சியமற்றசார்புகளாகவோ, மாறிலி அல்லது மாறிலிகளற்ற சார்புகளாகவோ, நேரியலான அல்லது நேரியலற்ற சார்புகளாகவோ இருக்கலாம். ஒரு வகைக்கெழுச் சமன்பாடு நேரியலானதா என்பதை உறுதிப்படுத்த, ஒரு சார்பு y(x) மற்றும் அதனுடைய வகைக்கெழுக்கள் மட்டுமே பயன்படுத்தப்படுகின்றன. 

வரையறை 10.7:

நேரியல் அல்லாத ஒரு வகைக்கெழுச் சமன்பாடு நேரியலற்ற வகைக்கெழுச் சமன்பாடு எனப்படும்.

ஒரு வகைக்கெழுச் சமன்பாட்டில், y,y',y",..., yn) கெழுக்களில் சார்ந்த மாறி y அல்லது அதனுடைய வகைக்கெழுக்கள் அல்லது y,y',y",...,y(n), (y')2 போன்ற அடுக்குகள் இடம்பெற்றிருந்தால் அவ்வகைக்கெழுச் சமன்பாடு நேரியலற்ற வகைக்கெழுச் சமன்பாடாகும்.

எடுத்துக்காட்டாக

(1) dy/dx = ax3 , d2y/dx2 + 2dy/dx + y = 0 மற்றும் dy/dx + p(x)y = q(x) என்பன நேரியலான சாதாரணவகைக்கெழுச் சமன்பாடுகளாகும். ஆனால் y (dy/dx) + sin x = 0 என்பது நேரியல்பற்றவகைக்கெழுச் சமன்பாடாகும்.

(2) y ′′ + 2x3y ′ = 7xy + x2 என்பது இரண்டாம் வரிசை நேரியலான சாதாரண இருபடி வகைக்கெழுச் சமன்பாடாகும்.

 (3) y ′′ + y′ = √x என்பது இரண்டாம் வரிசை நேரியலான சாதாரண வகைக்கெழுச் சமன்பாடாகும்.

 (4) y 2 + y′ = √x என்பது முதல் வரிசை நேரியல்பற்ற சாதாரண வகைக்கெழுச் சமன்பாடாகும். 

(5) y ′ = x sin( y) என்பது முதல் வரிசை நேரியல்பற்ற சாதாரண வகைக்கெழுச் சமன்பாடாகும். 

(6) y ′′ = y sin( x) என்பது இரண்டாம் வரிசை நேரியலான சாதாரண வகைக்கெழுச்சமன்பாடாகும். 

 வரையறை 10.8:

சமன்பாடு (1)இல் g(x) = 0 எனில், அச்சமன்பாடு சமப்படித்தான சமன்பாடு எனப்படும். அவ்வாறில்லையெனில் அச்சமன்பாடு சமபடியற்ற சமன்பாடு எனப்படும்.

 குறிப்புரை 

an (x) y (n) (x) + an −1 (x) y (n−1) (x) +. . . + a1 (x) y '(x) + a0 (x) y ( x) = 0       …(2)

எனும் சமன்பாட்டின் இரண்டு தீர்வுகள் yi,(x), i =1,2 எனில்,

an (x) yi( n) (x) + an −1 (x) yi( n−1) (x) + . . . + a1 (x) yi (x) + a0 (x) yi (x) = 0, i = 1, 2 . ஆகும்.

u ( x) = c1 y1 (x ) + c2 y2 (x) இங்கு c1, c2 என்பன ஏதேனும் இரு மாறிலிகள் என்க. பின்னர், u(x) என்பதும் சமன்பாடு (2)-ன் தீர்வாகும் என்பதை எளிதில் சரிபார்க்கலாம்.

ஆகவே, முதல் வரிசை நேரியலான வகைக்கெழுச் சமன்பாட்டை y’ + p(x)y = f (x) என எழுதலாம். அவ்வாறு எழுத முடியாத முதல் வரிசை வகைக்கெழுச் சமன்பாடு நேரியலற்றதாகும். y = 0 என்பது y' + p(x)y = 0 எனும் சமபடித்தான சமன்பாட்டின் தீர்வு எனத் தெளிவாக தெரிவதால், இத்தீர்வினை வெளிப்படைத் தீர்வு என அழைக்கிறோம். இச்சமன்பாட்டின் மற்ற தீர்வுகளை வெளிப்படையற்ற தீர்வுகள் என்போம். இது பொதுவான நேரியல் வகைக்கெழுச் சமன்பாடுகளுக்கும் உண்மையாகும்.