முதல் வரிசை நேரியல் வகைக்கெழுச் சமன்பாடுகள் (First Order Linear Differential Equations)

முதல் வரிசை நேரியல் வகைக்கெழுச் சமன்பாடுகள் (First Order Linear Differential Equations) 

முதல் வரிசை நேரியல் வகைக்கெழுச் சமன்பாட்டின் வடிவம் 

dy/dx + py = Q…… (1)

ஆகும். இங்கு P மற்றும் Q என்பன x-ல் மட்டுமே உள்ள சார்புகளாகும். இச்சமன்பாட்டில் y மற்றும் அதன் வகைக்கெழு dy/dx இவ்விரண்டின் பெருக்கல் பலன் இருக்காது. மேலும் சார்ந்த மாறி y மற்றும் சாராமாறி x ஐப் பொருத்த அதனுடைய வகைக்கெழு ஆகியவை முதலாம் படியாக மட்டுமே காணப்படும். 

சமன்பாடு (1)-ன் தீர்வு காண்பதற்கு முதலில் dy/dx + Py = 0       ----- (2)

எனும் சமபடித்தான சமன்பாட்டை எடுத்துக் கொள்வோம். 

சமன்பாடு (2)-ன் தீர்வினை பின்வருமாறு காணலாம்:

மாறிலிகளைப் பிரித்து எழுத, dy/y = -Pdx .

தொகையிட, நமக்குக் கிடைப்பது 

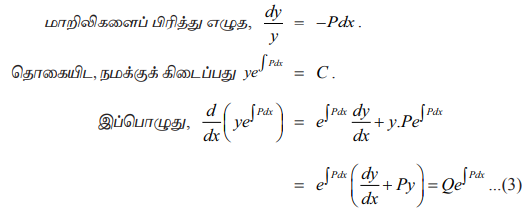
(சமன்பாடு (1)ஐப் பயன்படுத்த) 

சமன்பாடு (3)-ன் இருபக்கமும் xஐப் பொருத்து தொகையிட, கொடுக்கப்பட்ட வகைக்கெழுச் சமன்பாட்டின் தீர்வு

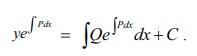எனக் கிடைக்கிறது.

இங்கு e∫Pdx  என்பது சமன்பாடு (1)-ன் தொகையீட்டுக் காரணி (தொ.கா) எனப்படும்.

குறிப்புரை

 1. நேரியல் வகைக்கெழுச் சமன்பாட்டின் தீர்வு

y × (தொ.கா) = ∫Q(தொ.கா)dx + C ஆகும். இங்கு C என்பது எதேச்சை மாறிலி. 

2. கொடுக்கப்பட்ட வகைக்கெழுச் சமன்பாட்டில் காணப்படும் dy/dx-ன் கெழு 1 என இருக்கும்போது, தொகையீட்டுக் காரணி e∫ Pdx-ல் உள்ள P என்பது y-ன் கெழுவாகும்.

3. dx/dy + Px = Q என்ற முதல் வரிசை நேரியல் சமன்பாட்டில் P மற்றும் Q என்பன y-ல் மட்டுமே உள்ள சார்புகளாகும். இச்சமன்பாட்டில் x  மற்றும் dx/dy இவ்விரண்டும் பெருக்கலாக இருக்காது. மேலும் சார்ந்த மாறி x மற்றும் சாராமாறி y ஐப் பொருத்த அதன் வகைக் கெழு ஆகியவற்றின் படி 1 ஆக மட்டுமே காணப்படும்.

இவ்வகையில், வகைக்கெழுச் சமன்பாட்டின் தீர்வு  xe∫ Pdy = ∫Qe∫ Pdy dy + C . ஆகும்.