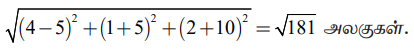வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் - ஒரு புள்ளியிலிருந்து தளத்திற்குள்ள தொலைவு (Distance of a point from a plane) | 12th Maths : UNIT 6 : Applications of Vector Algebra

12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்

ஒரு புள்ளியிலிருந்து தளத்திற்குள்ள தொலைவு (Distance of a point from a plane)

ஒரு புள்ளியிலிருந்து தளத்திற்குள்ள தொலைவு (Distance of a point from a plane) (a) தளத்தின் வெக்டர் சமன்பாடு (Vector form of equation) (b) தளத்தின் கார்டீசியன் சமன்பாடு (Cartesian form of equation)

12. ஒரு புள்ளியிலிருந்து தளத்திற்குள்ள தொலைவு (Distance of a point from a plane)

(a) தளத்தின் வெக்டர் சமன்பாடு (Vector form of equation)

தேற்றம் 6.20

என்ற நிலைவெக்டர் கொண்ட புள்ளியிலிருந்து 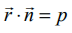என்ற தளத்திற்கு உள்ள செங்குத்துத் தொலைவு

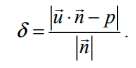
நிரூபணம்

A என்ற புள்ளியின் நிலை வெக்டர் என்க.

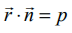என்ற தளத்திற்கு A என்ற புள்ளியிலிருந்து வரையப்பட்ட செங்குத்தின் அடி F என்க. F மற்றும் A ஆகியவற்றை இணைக்கும் கோடானது தளத்தின் செங்கோடு –க்கு இணையாகும். எனவே, FA−ன் சமன்பாடு 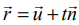ஆகும்.

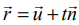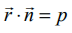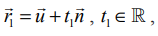ஆனால், F என்பது என்ற கோடும் என்ற தளமும் வெட்டிக்கொள்ளும் புள்ளியாகும். என்பது F−ன் நிலைவெக்டர் எனில், மற்றும் 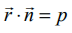ஆகும். இச்சமன்பாடுகளிலிருந்து −ஐ நீக்க, நாம் பெறுவது

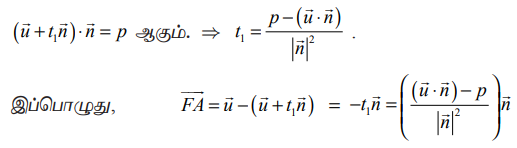
எனவே, A என்ற புள்ளியிலிருந்து கொடுக்கப்பட்ட தளத்திற்குள்ள செங்குத்துத் தொலைவு

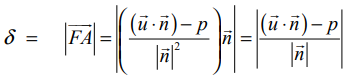
AF என்ற செங்குத்தின் அடி F –ன் நிலைவெக்டர்

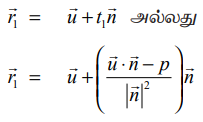
(b) தளத்தின் கார்டீசியன் சமன்பாடு (Cartesian form of equation)

என்ற கொடுக்கப்பட்ட நிலைவெக்டரைக் கொண்ட புள்ளி A (x1,y1,z1) மற்றும் கொடுக்கப்பட்ட தளத்தின் கார்டீசியன் சமன்பாடு ax+by+cz = p எனில், 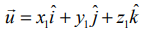மற்றும் 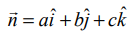ஆகும்.

இவ்வெக்டர்களை 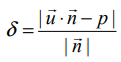–ல் பிரதியிட, கொடுக்கப்பட்ட தளத்திற்குள்ள செங்குத்துத் தொலைவு

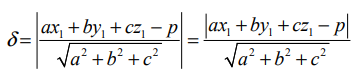எனப் பெறுகிறோம்.

குறிப்புரை

ஆதிப்புள்ளியிலிருந்து ax + by + cz + d = 0 என்ற தளத்திற்குள்ள செங்குத்துத் தொலைவு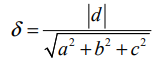

எடுத்துக்காட்டு 6.49

(2,5,−3) என்ற புள்ளியிலிருந்து 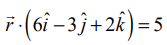என்ற தளத்திற்குள்ள தொலைவுக் காண்க.

தீர்வு

எடுத்துக்காட்டு 6.50

A (4,1,2) மற்றும் B (7,5,4) ஆகிய புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோடும் x – y + z = 5 என்ற தளமும் வெட்டிக் கொள்ளும் புள்ளிக்கும் (5,−5,−10) என்ற புள்ளிக்கும் உள்ள தொலைவைக் காண்க.

தீர்வு

A (4,1,2) மற்றும் B (7,5,4) ஆகிய புள்ளிகளை இணைக்கும் கோட்டின் சமன்பாடு

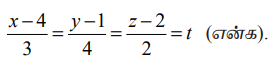
இக்கோட்டின் மீதுள்ள ஏதேனும் ஒரு புள்ளி (3t+4,4t+1,2t+2) ஆகும். கோடும் தளமும் வெட்டிக் கொள்ளும் புள்ளியைக் காண, x = 3t + 4, y = 4t + 1, z = 2t + 2 என x−y+z=5−ல் பிரதியிட்டு t =0 எனப் பெறுகிறோம். எனவே, நேர்க்கோடும் தளமும் வெட்டிக்கொள்ளும் புள்ளி (4, 1, 2) ஆகும். ஆகவே, (4, 1, 2) மற்றும் (5,−5,−10) ஆகிய புள்ளிகளுக்கு இடைப்பட்ட தொலைவு

Tags : Definition, Theorem, Proof, Solved Example Problems, Solution வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள்.

12th Maths : UNIT 6 : Applications of Vector Algebra : Distance of a point from a plane Definition, Theorem, Proof, Solved Example Problems, Solution in Tamil : 12th Standard TN Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் : ஒரு புள்ளியிலிருந்து தளத்திற்குள்ள தொலைவு (Distance of a point from a plane) - வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் : 12 ஆம் வகுப்பு தமிழ்நாடு பள்ளி சமசீர் புத்தகம் கேள்விகள் மற்றும் பதில்கள்.