சமதள முன்னேறு அலைக்கான சமன்பாடு

சமதள முன்னேறு அலைக்கான சமன்பாடு

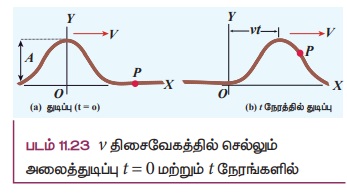
t = 0 S ல் இழுத்துக் கட்டப்பட்ட கம்பியை சட்டென இழுத்துவிடு. படம் 11.23 (a) இல் கொடுக்கப்பட்ட மாறுபாட்டினால் ஏற்பட்ட துடிப்பு நேர்க்குறி x திசையில் நிலையான வேகம் v ல் முன்னேறிச் செல்கிறது. 

அலைத்துடிப்பின் வடிவத்தை கணிதமுறையில் t = 0 வினாடியில் y = y(x, 0) = f(x) என குறிக்கலாம். அலைத்துடிப்பின் வடிவம் அதன் முன்னேறும் பாதையில் மாறாது எனக் கருதுவோம். சிறிதுநேரம் t க்கு பிறகு, வலப்பக்கம் நகர்த்த துடிப்பை x' எனக் குறிப்போம் (x prime என வாசிக்கவும்) படம் 11.23 (b) இல் காட்டியுள்ளவாறு

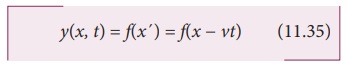
இதேபோல், அலைத்துடிப்பு நிலையான திசைவேகம் v யுடன் இடப்பக்கம் இயங்குவதாகக் கருதினால்,  y = f(x + vt).

இரு அலைகள் y = f(x + vt) யும் y = f(x − vt) கீழ்க்கண்ட ஒரு பரிமாண வகைக்கெழு சமன்பாட்டிற்கு பொருந்தும்; அதுவே அலைச் சமன்பாடு எனப்படுகிறது.

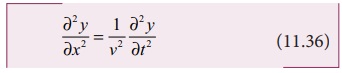
இங்கு குறியீடு ∂ பகுதி வகைக் கெழுவைக் (partial derivative) குறிக்கிறது. மேற்கண்ட சமன்பாட்டின் அனைத்து தீர்வுகளும் அலைக்கு பொருந்தாது; ஏனெனில் எந்த ஒரு ஏற்கக்கூடிய அலையும் நிலையான மதிப்புகளை அனைத்து x மற்றும் t க்கு பெற வேண்டும். ஆனால், ஒரு சார்பு ஒரு அலையை குறித்தால், அது மேற்கண்ட வகைக்கெழு சமன்பாட்டிற்கு பொருந்த வேண்டும். ஒரு பரிமாணத்தில் (ஒரு தனிப்பட்ட மாறி), x - ஐப் பொருத்த மொத்த வகைக்கெழுவும் பகுதி வகைக்கெழுவும் ஒன்றே; அதை

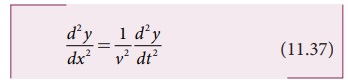
இதை ஒரு பரிமாணத்திற்கு மேலும் (இரண்டு, மூன்று, மேலும் ....) எழுதலாம். எளிமைக்காக ஒரு பரிமாண அலைச்சமன்பாட்டை மட்டும் கருதுவோம்.

எடுத்துக்காட்டு 11.11

வெவ்வேறு a மதிப்புகளுக்கு y = x −a என்ற கோட்டினை வரைக. 

தீர்வு :

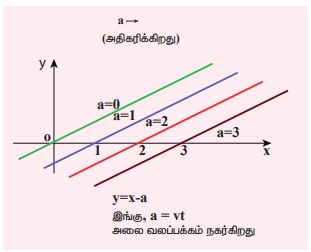
இதிலிருந்து நாம் அறிவது, a மதிப்பை அதிகரிக்கும் போது, கோடானது வலப்பக்கம் நகர்கிறது. a = vt, y = x − vt வகைக்கெழு சமன்பாட்டிற்கு பொருந்துகிறது. இந்த சார்பு, வகைக்கெழு சமன்பாட்டிற்கு பொருந்தினாலும், இது x மற்றும் t க்கான அனைத்து மதிப்புகளுக்கும் நிலையாக இல்லை. எனவே, இது அலையை குறிக்கவில்லை. எனவே, இந்தச் சார்பு ஒரு அலையைக் குறிக்கவில்லை.

எடுத்துக்காட்டு 11.12 

y = sin(x − a) f என்ற அலை a = 0, a = π/4, a = π/2, a = 3π/2, மற்றும் a = π என்ற மதிப்புகளுக்கு எவ்வாறு இருக்கிறது என வரைபடங்கள் மூலம் காட்டுக.

தீர்வு :

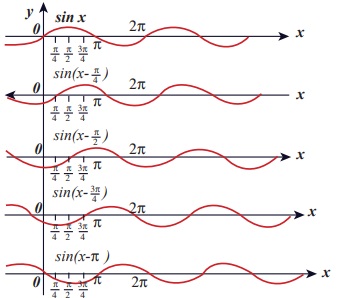
மேற்கண்ட படங்களிலிருந்து நாம் அறிவது y = sin (x−a) ; a = 0, a = π/4, a = π/2, a = 3π/2 , a = π, க்கு வரையப்பட்டுள்ளது. y = sin (x−a) ஆனது வலப்பக்கம் நகர்கிறது. 

மேலும் a = vt மற்றும் v = π/4, என எடுத்துக்கொண்டு t = 0s, t = 1s, t = 2s எனப் பொருத்தி வரைபடம் வரைந்தால், மீண்டும் y = sin(x−vt) வலப்பக்கம் நகர்கிறது. எனவே, y = sin(x−vt) என்பது ஒரு பயணிக்கும் அல்லது முன்னேறு அலை. இது வலப்பக்கம் நகர்கிறது. 

y = sin(x+vt) எனக் கொண்டால் முன்னேறு (பயணிக்கும்) அலை இடப்பக்கம் நகர்கிறது. இதனால் சார்பு y = f(x−vt) என்பது அலை வலப்பக்கம் நகர்வதையும், சார்பு y = f(x+vt) என்பது அலை இடப்பக்கம் நகர்வதையும் குறிக்கிறது.

எடுத்துக்காட்டு 11.13

அலை y = sin(x-vt) யை பரிமாணப் பகுப்பாய்வு மூலம் சரிபார். பரிமாண முறையில் தவறு எனில் மேற்கண்ட சமன்பாட்டை சரியான முறையில் எழுது. 

தீர்வு :

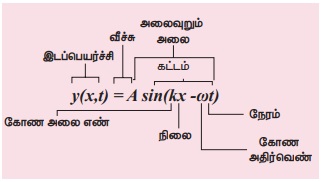
பரிமாண முறையில் தவறு y = sin(x-vt) என்பது பரிமாணமற்ற அளவாக அமைய வேண்டும். ஆனால், x-vt சரியான சமன்பாடு y = sin (kx-wt), இங்கு k ன் பரிமாணம், நீளத்தின் பரிமாணத்தின் தலைகீழாக இருக்கும்; ω வின் பரிமாணங்கள் நேரத்தின் பரிமாணம் தலைகீழாக இருக்கும். சைன் சார்பும், கொசைன் சார்பும் சீரான நேர முறையில் மாறும் சார்பு. இங்கு நேரம் 2π யாக உள்ளது. எனவே சரியான தொடர்பு y = sin ([2π/λ]x, [2π/T]t) இங்கு λ மற்றும் T முறையே அலைநீளம், அலைவுநேரம். பொதுவாக y(x,t)=A sin(k x−ωt).