முன்னேறு அலை அல்லது இயங்கும் அலை

முன்னேறு அலை அல்லது இயங்கும் அலை :

அலை ஒன்று ஊடகத்தில் தொடர்ந்து முன்னேறிச் சென்றால் அந்த அலை முன்னேறு அலை அல்லது இயங்கும் அலை என்று பெயர்.

முன்னேறு அலையின் பண்புகள் :

1. ஊடகத் துகள்கள் அதன் சமநிலைப்புள்ளியை மையமாகக் கொண்டு மாறாத வீச்சில் அதிர்வுறுகின்றன. 

2. ஒவ்வொரு துகளின் கட்டமும் 0 முதல் 2π  வரை மாறுகின்றன. 

3. எந்தவொரு துகளும் தொடர்ந்து ஓய்வில் இருப்பதில்லை. அலை முன்னேறும் போது ஒவ்வொரு கடைநிலை புள்ளிகளில் மட்டும் இருமுறை ஓய்வு நிலைக்கு வருகின்றன. 

4. முன்னேறு குறுக்கலைகள் முகடுகள் அகடுகளாகவும், முன்னேறு நெட்டலைகள் இறுக்கங்கள், தளர்ச்சிகளாகவும் பரவுகின்றன.

5. துகள்கள் சமநிலைப்புள்ளியை கடக்கும் போது சமஅளவு பெரும திசைவேகத்தில் செல்கின்றன. 

6. nλ தொலைவில் (n - ஒரு முழு எண்)பிரிக்கப்பட்ட துகள்களின் இடப்பெயர்ச்சி, திசைவேகம், முடுக்கம் சமமாகும்.

சமதள முன்னேறு அலைக்கான சமன்பாடு

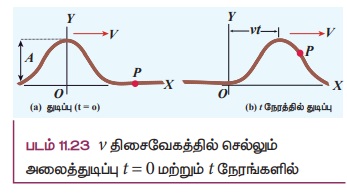
t = 0 S ல் இழுத்துக் கட்டப்பட்ட கம்பியை சட்டென இழுத்துவிடு. படம் 11.23 (a) இல் கொடுக்கப்பட்ட மாறுபாட்டினால் ஏற்பட்ட துடிப்பு நேர்க்குறி x திசையில் நிலையான வேகம் v ல் முன்னேறிச் செல்கிறது. 

அலைத்துடிப்பின் வடிவத்தை கணிதமுறையில் t = 0 வினாடியில் y = y(x, 0) = f(x) என குறிக்கலாம். அலைத்துடிப்பின் வடிவம் அதன் முன்னேறும் பாதையில் மாறாது எனக் கருதுவோம். சிறிதுநேரம் t க்கு பிறகு, வலப்பக்கம் நகர்த்த துடிப்பை x' எனக் குறிப்போம் (x prime என வாசிக்கவும்) படம் 11.23 (b) இல் காட்டியுள்ளவாறு

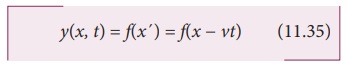
இதேபோல், அலைத்துடிப்பு நிலையான திசைவேகம் v யுடன் இடப்பக்கம் இயங்குவதாகக் கருதினால்,  y = f(x + vt).

இரு அலைகள் y = f(x + vt) யும் y = f(x − vt) கீழ்க்கண்ட ஒரு பரிமாண வகைக்கெழு சமன்பாட்டிற்கு பொருந்தும்; அதுவே அலைச் சமன்பாடு எனப்படுகிறது.

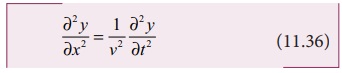
இங்கு குறியீடு ∂ பகுதி வகைக் கெழுவைக் (partial derivative) குறிக்கிறது. மேற்கண்ட சமன்பாட்டின் அனைத்து தீர்வுகளும் அலைக்கு பொருந்தாது; ஏனெனில் எந்த ஒரு ஏற்கக்கூடிய அலையும் நிலையான மதிப்புகளை அனைத்து x மற்றும் t க்கு பெற வேண்டும். ஆனால், ஒரு சார்பு ஒரு அலையை குறித்தால், அது மேற்கண்ட வகைக்கெழு சமன்பாட்டிற்கு பொருந்த வேண்டும். ஒரு பரிமாணத்தில் (ஒரு தனிப்பட்ட மாறி), x - ஐப் பொருத்த மொத்த வகைக்கெழுவும் பகுதி வகைக்கெழுவும் ஒன்றே; அதை

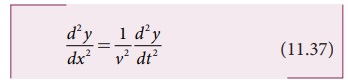
இதை ஒரு பரிமாணத்திற்கு மேலும் (இரண்டு, மூன்று, மேலும் ....) எழுதலாம். எளிமைக்காக ஒரு பரிமாண அலைச்சமன்பாட்டை மட்டும் கருதுவோம்.

எடுத்துக்காட்டு 11.11

வெவ்வேறு a மதிப்புகளுக்கு y = x −a என்ற கோட்டினை வரைக. 

தீர்வு :

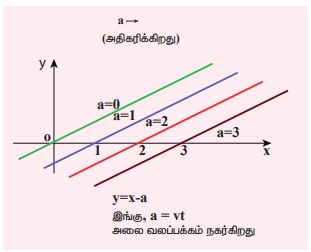
இதிலிருந்து நாம் அறிவது, a மதிப்பை அதிகரிக்கும் போது, கோடானது வலப்பக்கம் நகர்கிறது. a = vt, y = x − vt வகைக்கெழு சமன்பாட்டிற்கு பொருந்துகிறது. இந்த சார்பு, வகைக்கெழு சமன்பாட்டிற்கு பொருந்தினாலும், இது x மற்றும் t க்கான அனைத்து மதிப்புகளுக்கும் நிலையாக இல்லை. எனவே, இது அலையை குறிக்கவில்லை. எனவே, இந்தச் சார்பு ஒரு அலையைக் குறிக்கவில்லை.

எடுத்துக்காட்டு 11.12 

y = sin(x − a) f என்ற அலை a = 0, a = π/4, a = π/2, a = 3π/2, மற்றும் a = π என்ற மதிப்புகளுக்கு எவ்வாறு இருக்கிறது என வரைபடங்கள் மூலம் காட்டுக.

தீர்வு :

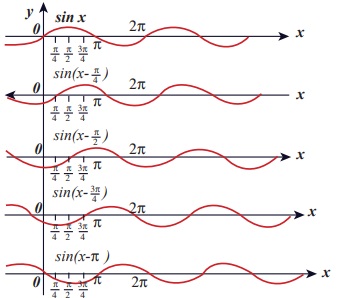
மேற்கண்ட படங்களிலிருந்து நாம் அறிவது y = sin (x−a) ; a = 0, a = π/4, a = π/2, a = 3π/2 , a = π, க்கு வரையப்பட்டுள்ளது. y = sin (x−a) ஆனது வலப்பக்கம் நகர்கிறது. 

மேலும் a = vt மற்றும் v = π/4, என எடுத்துக்கொண்டு t = 0s, t = 1s, t = 2s எனப் பொருத்தி வரைபடம் வரைந்தால், மீண்டும் y = sin(x−vt) வலப்பக்கம் நகர்கிறது. எனவே, y = sin(x−vt) என்பது ஒரு பயணிக்கும் அல்லது முன்னேறு அலை. இது வலப்பக்கம் நகர்கிறது. 

y = sin(x+vt) எனக் கொண்டால் முன்னேறு (பயணிக்கும்) அலை இடப்பக்கம் நகர்கிறது. இதனால் சார்பு y = f(x−vt) என்பது அலை வலப்பக்கம் நகர்வதையும், சார்பு y = f(x+vt) என்பது அலை இடப்பக்கம் நகர்வதையும் குறிக்கிறது.

எடுத்துக்காட்டு 11.13

அலை y = sin(x-vt) யை பரிமாணப் பகுப்பாய்வு மூலம் சரிபார். பரிமாண முறையில் தவறு எனில் மேற்கண்ட சமன்பாட்டை சரியான முறையில் எழுது. 

தீர்வு :

பரிமாண முறையில் தவறு y = sin(x-vt) என்பது பரிமாணமற்ற அளவாக அமைய வேண்டும். ஆனால், x-vt சரியான சமன்பாடு y = sin (kx-wt), இங்கு k ன் பரிமாணம், நீளத்தின் பரிமாணத்தின் தலைகீழாக இருக்கும்; ω வின் பரிமாணங்கள் நேரத்தின் பரிமாணம் தலைகீழாக இருக்கும். சைன் சார்பும், கொசைன் சார்பும் சீரான நேர முறையில் மாறும் சார்பு. இங்கு நேரம் 2π யாக உள்ளது. எனவே சரியான தொடர்பு y = sin ([2π/λ]x, [2π/T]t) இங்கு λ மற்றும் T முறையே அலைநீளம், அலைவுநேரம். பொதுவாக y(x,t)=A sin(k x−ωt).

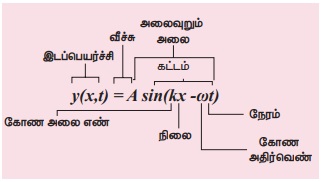
அலை ஒன்றின் வரைபட வடிவம் 

கீழ்க்கண்ட இரு வடிவ அலைமாறுபாடுகளை வரைப்படமாக காட்டுவோம். 

(அ) வெளி (அல்லது இடஞ்சார்ந்த) மாறுபாடு வரைபடம் (space variation graph) 

(ஆ) காலம் (அல்லது நேரம் சார்ந்த) மாறுபாடு வரைபடம் (time variation graph)

(அ) வெளி மாறுபாடு வரைபடம் :

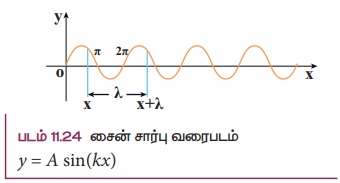
படம் 11.24 சைன் சார்பு வரைபடம் y = A sin(kx) நேரத்தை நிலையாகக் கொண்டு x யைப் பொறுத்து இடப்பெயர்ச்சி மாறுபாடு வரையப்பட்டுள்ளது. y = A sin(kx) என்ற சைன் சார்பு வரைகோடு படம் 11.24 ல் காட்டப்பட்டுள்ளதை கருதுவோம். இங்கு k ஒரு மாறிலி λ அலைநீளம் என்பது ஒரே அதிர்வு நிலையில் உள்ள இரு அடுத்தடுத்த புள்ளிகளுக்கிடையேயானத் தொலைவு. y=x மற்றும் y = x + λ, என்ற இரு முனைகளிலும் இடப்பெயர்ச்சி y ஆனது ஒரே அளவு. அதாவது, 

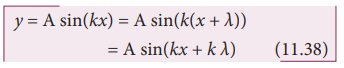
சைன் சார்பு ஒரு சீரான நேர முறையில் மாறும் (இங்கு நேரம் 2 π) எனவே,

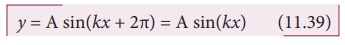
சமன்பாடு (11.38), (11.39)யை ஒப்பிட,

kx + k λ = kx + 2π 

இது காட்டுகிறது 

இங்கு k என்பது அலை எண். இது 2π ரேடியனில் எத்தனை அலைகள் உள்ளன எனக் காணவும் அல்லது எவ்வளவு வேகமாக அலை, வெளியில் அலைவுறுகிறது எனக் காணவும் பயன்படுகிறது. அலையின் வெளிச்சார்ந்த முறையான அதிர்வு (Periodicity)

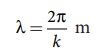
t = 0 s  ல்   y(x, 0) = y(x + λ, 0)

ஏதேனும் ஒரு நேரம் t யில் y(x, t) = y(x + λ, t) 

எடுத்துக்காட்டு 11.14

இரு அலைகளின் அலைநீளங்கள் முறையே λ1 = 1m, λ2 = 6m எனில் அவற்றின் அலை எண்களைக் காண்க. 

தீர்வு :

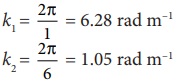
(ஆ) நேர மாறுபாடு வரைபடம் (time variation graph)

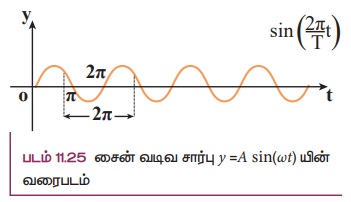
நிலை மாறாமல் உள்ள போது, நேரத்தைப் பொருத்து , இடப்பெயர்ச்சியில் ஏற்படும் மாறுபாடு வரைபடமாக வரையப்பட்டுள்ளது. படம் 11.25 ல் காட்டியவாறு y = A sin(ωt) என்ற சைன் சார்பு வரைப்படத்தைக் கருதுவோம். இங்கு ω கோண அதிர்வெண். இது நேரத்தைப் பொறுத்து எவ்வளவு விரைவாக அலை அலைவுறுகிறது அல்லது ஒரு வினாடிக்கு எத்தனை சுழற்சிகள் ஏற்படுகிறது என்பதைக் காட்டுகிறது. நேரஞ்சார்ந்த இடைவெளி விரைவதிர்வு (Periodicity)

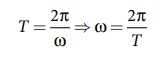
கோண அதிர்வெண், அதிர்வெண்ணுடன் கீழ்க்கண்டவாறு தொடர்புபடுத்தப்பட்டுள்ளது. ω = 2 πf, இங்கு f அதிர்வெண் ஊடகத்துகள் ஒரு விநாடியில்  ஏற்படுத்தும் அலைவுகளின் எண்ணிக்கை என வரையறுக்கப்படுகிறது. அதிர்வெண்ணின் தலைகீழி அலைவுநேரமாதலால்,

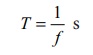
T ஊடகத்துக்கள் ஒரு அலைவை (அதிர்வை ) முடிப்பதற்கான நேரம். எனவே, அலையின் வேகத்தை, அலை 1 விநாடியில் கடக்கும் தொலைவு என வரையறுக்கலாம்.

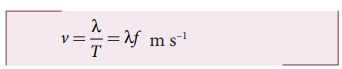
இது சமன்பாடு (11.4)ல் கிடைத்த அதே தொடர்பு.

துகள் திசைவேகம் மற்றும் அலை திசைவேகம்:

சமதள முன்னேறு அலையில் (சீரிசை) ஊடகத்தின் துகள்கள் அவற்றின் சமநிலைப்புள்ளியை மையமாகக் கொண்டு தனிச்சீரிசையில் அலைவுறுகின்றன. துகள் ஒன்று இயக்கத்திலுள்ள போது, எந்த ஒரு கணத்திலும் அதன் இடப்பெயர்ச்சி மாறும் வீதம் திசைவேகம் என வரையறுக்கப்படுகிறது. இதுவே துகளின் திசைவேகம்

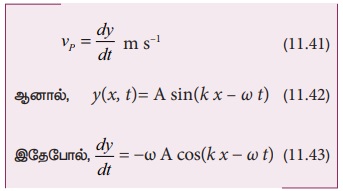
இதேபோல் முன்னேறு (இயங்கும்) அலையின் திசைவேகத்தை (இங்கு வேகம்) வரையறுக்கலாம். படம் 11.23 இல் காட்டியவாறு ஒரு முன்னேறு அலையைக் கருதுவோம். இது வலப்பக்கம் நோக்கி இயங்குகிறது என்க. கணித வடிவில் ஒரு சைன் அலையாகக் காட்டலாம். P என்பது அதன் கட்டத்தில் ஓர்புள்ளிஎன்க. yp என்பது சமநிலையிலிருந்து அதன் இடப்பெயர்ச்சி என்க. எந்தவொரு கணத்திலும் (t) இடப்பெயர்ச்சியானது

y = y(x,t) = A sin(k x− ω t)

அடுத்த கணம்  tʹ = t + ∆t யில் P ன் நிலை xʹ = x + ∆x  என்க. இந்தப் புதிய கணத்தில் (t) இடப்பெயர்ச்சி

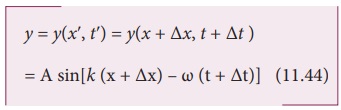
அலையின் வடிவம் மாறாதது; அதாவது அலையின் கட்டம் மாறாது (எனவே y இடப்பெயர்ச்சி ஒரு மாறிலி) எனவே (11.42) யும் (11.44) யும் சமப்படுத்த,

இங்கு vp அலையின் திசைவேகம் (wave velocity) அல்லது கட்ட திசைவேகம் (phase velocity).

கோண அதிர்வெண், அலை எண்களை அதிர்வெண் மற்றும் அலைநீளம் மூலம் எழுத, சமன்பாடு (11:46) மூலம் சமன்பாடு (11.43) யை பெறலாம். இதன் மூலம் கோண அதிர்வெண், அலை எண் மற்றும் திசைவேகங்களை கீழ்க்கண்டவாறு எழுதலாம்.

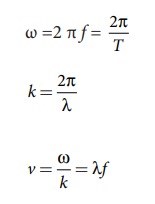
எடுத்துக்காட்டு 11.15

ஒரு கைபேசி 900MHz அதிர்வெண் உடைய சைகைகளை வெளிவிடுகிறது. கை பேசி கோபுரம் மூலம் வெளிவிடும் அலையின் அலை நீளம் காண்.

தீர்வு:

அதிர்வெண், f = 900 MHz = 900 ×106 Hz

அலையின் வேகம் c = 3 × 108m s-1