11வது இயற்பியல் : அலகு 11 : அலைகள்
அலை ஒன்றின் வரைபட வடிவம்
அலை ஒன்றின் வரைபட வடிவம்
கீழ்க்கண்ட இரு வடிவ அலைமாறுபாடுகளை வரைப்படமாக காட்டுவோம்.
(அ) வெளி (அல்லது இடஞ்சார்ந்த) மாறுபாடு வரைபடம் (space variation graph)
(ஆ) காலம் (அல்லது நேரம் சார்ந்த) மாறுபாடு வரைபடம் (time variation graph)
(அ) வெளி மாறுபாடு வரைபடம் :
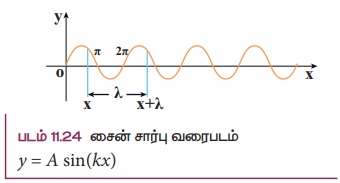
படம் 11.24 சைன் சார்பு வரைபடம் y = A sin(kx) நேரத்தை நிலையாகக் கொண்டு x யைப் பொறுத்து இடப்பெயர்ச்சி மாறுபாடு வரையப்பட்டுள்ளது. y = A sin(kx) என்ற சைன் சார்பு வரைகோடு படம் 11.24 ல் காட்டப்பட்டுள்ளதை கருதுவோம். இங்கு k ஒரு மாறிலி λ அலைநீளம் என்பது ஒரே அதிர்வு நிலையில் உள்ள இரு அடுத்தடுத்த புள்ளிகளுக்கிடையேயானத் தொலைவு. y=x மற்றும் y = x + λ, என்ற இரு முனைகளிலும் இடப்பெயர்ச்சி y ஆனது ஒரே அளவு. அதாவது,
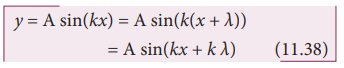
சைன் சார்பு ஒரு சீரான நேர முறையில் மாறும் (இங்கு நேரம் 2 π) எனவே,
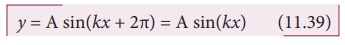
சமன்பாடு (11.38), (11.39)யை ஒப்பிட,
kx + k λ = kx + 2π
இது காட்டுகிறது

இங்கு k என்பது அலை எண். இது 2π ரேடியனில் எத்தனை அலைகள் உள்ளன எனக் காணவும் அல்லது எவ்வளவு வேகமாக அலை, வெளியில் அலைவுறுகிறது எனக் காணவும் பயன்படுகிறது. அலையின் வெளிச்சார்ந்த முறையான அதிர்வு (Periodicity)
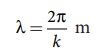
t = 0 s ல் y(x, 0) = y(x + λ, 0)
ஏதேனும் ஒரு நேரம் t யில் y(x, t) = y(x + λ, t)
எடுத்துக்காட்டு 11.14
இரு அலைகளின் அலைநீளங்கள் முறையே λ1 = 1m, λ2 = 6m எனில் அவற்றின் அலை எண்களைக் காண்க.
தீர்வு :
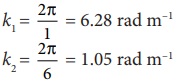
(ஆ) நேர மாறுபாடு வரைபடம் (time variation graph)
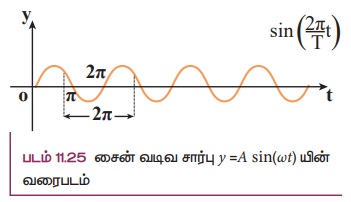
நிலை மாறாமல் உள்ள போது, நேரத்தைப் பொருத்து , இடப்பெயர்ச்சியில் ஏற்படும் மாறுபாடு வரைபடமாக வரையப்பட்டுள்ளது. படம் 11.25 ல் காட்டியவாறு y = A sin(ωt) என்ற சைன் சார்பு வரைப்படத்தைக் கருதுவோம். இங்கு ω கோண அதிர்வெண். இது நேரத்தைப் பொறுத்து எவ்வளவு விரைவாக அலை அலைவுறுகிறது அல்லது ஒரு வினாடிக்கு எத்தனை சுழற்சிகள் ஏற்படுகிறது என்பதைக் காட்டுகிறது. நேரஞ்சார்ந்த இடைவெளி விரைவதிர்வு (Periodicity)
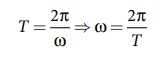
கோண அதிர்வெண், அதிர்வெண்ணுடன் கீழ்க்கண்டவாறு தொடர்புபடுத்தப்பட்டுள்ளது. ω = 2 πf, இங்கு f அதிர்வெண் ஊடகத்துகள் ஒரு விநாடியில் ஏற்படுத்தும் அலைவுகளின் எண்ணிக்கை என வரையறுக்கப்படுகிறது. அதிர்வெண்ணின் தலைகீழி அலைவுநேரமாதலால்,
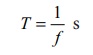
T ஊடகத்துக்கள் ஒரு அலைவை (அதிர்வை ) முடிப்பதற்கான நேரம். எனவே, அலையின் வேகத்தை, அலை 1 விநாடியில் கடக்கும் தொலைவு என வரையறுக்கலாம்.
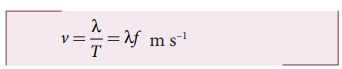
இது சமன்பாடு (11.4)ல் கிடைத்த அதே தொடர்பு.