நீட்டப்பட்ட கம்பியில் ஏற்படும் குறுக்கலையின் திசைவேகம்

இந்த பகுதியில், அலைகளின் திசைவேகத்தை இரு வேறு நிலைகளில் வருவிப்போம்: 

1. நீட்டப்பட்ட கம்பியில் ஏற்படும் குறுக்கலைகளின் திசைவேகம் 

2. மீட்சித்தன்மை கொண்ட ஊடகத்தில் நெட்டலைகளின் திசைவேகம்

1. நீட்டப்பட்ட கம்பியில் ஏற்படும் குறுக்கலையின் திசைவேகம்

கம்பி ஒன்றில் இயங்கும் குறுக்கலையின் திசைவேகத்தை கணக்கிடுவோம். கம்பியின் இடது முனையை மேல்நோக்கி சொடுக்கினால், அந்த துடிப்பு வலது முனை நோக்கி v என்ற திசைவேகத்தில் பொருள் ஓய்வு நிலையில் உள்ள குறிப்பாயத்தில் உள்ள பார்வையாளரைப் பொருத்து, நகர்கிறது. 

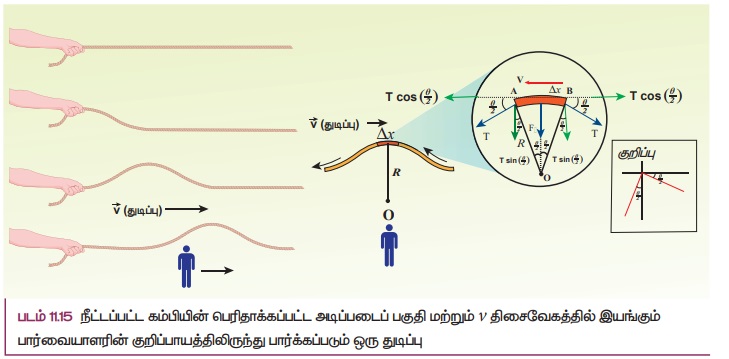
படம் 11.15 ல் காட்டியவாறு கம்பியில் ஒரு அடிப்படைப் பகுதியைக் கருதுவோம். கம்பியில் A, B என்ற புள்ளிகளை இக்கணத்தில் கருதுவோம். dI, dm என்பது கம்பியின் சிறுபகுதி நீளம் மற்றும் நிறை என்போம். வரையறையின்படி நீள் நிறை அடர்த்தி (μ) ஆனது பின்வருமாறு எழுதப்படுகிறது.

படத்தில் காட்டியவாறு அடிப்படை பகுதி AB ஆனது வட்டத்தின் ஒரு பகுதி போல், O வை மையமாக கொண்டு R ஆரத்துடன் வளைந்து கோணம்  θ வை வளைகோடு மையம் O வில் ஏற்படுத்துகிறது. θ வை வளைகோடு AB ன் நீளம் dl மற்றும் ஆரம் R யைப் பயன்படுத்தி பின்வருமாறு எழுதலாம்.

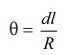
கம்பியின் இழுவிசை தரும் மையநோக்கு முடுக்கம் (எண்மதிப்பு)

மைய நோக்கு விசை

சமன்பாடு (11.6) லிருந்து,

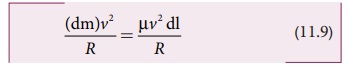
இழுவிசை T ஆனது, கம்பியின் சிறுபகுதி நீளம் AB யின் தொடுகோட்டின் வழியே செயல்படுகிறது. வளைகோடு AB யின் நீளம் மிகச்சிறியது. எனவே இழுவிசை T யில் ஏற்படும் மாறுபாடு புறக்கணிக்கத்தக்கது.

இழுவிசையை T யை கிடைமட்டக்கூறு Tcos(θ/2) மற்றும் செங்குத்துக்கூறு T sin(θ/2) என இரு கூறுகளாகப் பகுக்கலாம். A, B யில் கிடைமட்டக் கூறுகள் சம எண்மதிப்பில் எதிர்திசையில் செயல்படுகின்றன. எனவே, அவை ஒன்றை ஒன்று சமன் செய்கின்றன. நீளம் AB யை மிகச்சிறியதாக கருதுவதால், செங்குத்துக்கூறுகள் A, B யில் செங்குத்து திசையில் வளைவின் மையம் நோக்கி இருப்பதால் அவற்றைக் கூட்ட வேண்டும். தொகுபயன் ஆர விசை Fr ஆனது

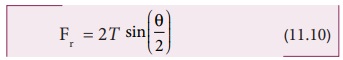
கம்பியின் நீளத்துடன் ஒப்பிட, அலையின் வீச்சு மிகச்சிறியது. எனவே,  sin(θ/2)≈ θ/2. எனவே,

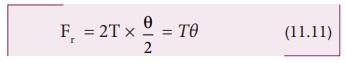
ஆனால், θ =  dl/R, எனவே நாம் பெறுவது

நியூட்டனின் இரண்டாவது விதியை கம்பியின் சிறுபகுதி நீளத்திற்கு ஆர வழியே செயல்படுத்த, சமநிலையில் விசையின் ஆரத்திசை கூறு (radial), மைய நோக்கு விசைக்கு சமமாகும். சமன்பாடு (11.9) மற்றும் (11.12) ஐ சமப்படுத்த, கிடைப்பது

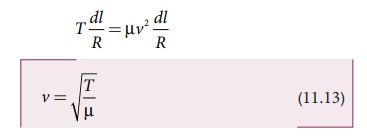
காட்சிப்பதிவுகள் :

• கம்பியில் ஏற்படும் அலையின் திசைவேகம் 

அ இழுவிசையின் இருமடி மூலத்திற்கு நேர்த்தகவிலும்

ஆ நீள் நிறை அடர்த்தி (linear mass density) யின் இருமடி மூலத்திற்கு எதிர்த்தகவிலும் 

இ அலை வடிவத்தைச் சாராமலும் அமையும்

எடுத்துக்காட்டு 11.6

படத்தில் காட்டியபடி நீள் நிறை அடர்த்தி 0.25 kg m-1 கொண்ட கம்பியில் இயக்கத்தில் உள்ள துடிப்பின் திசைவேகம் காண்க. மேலும் துடிப்பு 30 cm யைக் கம்பியில் கடக்க எடுத்துக்கொள்ளும் நேரத்தையும் காண்க.

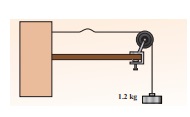
தீர்வு : 

கம்பியின் இழுவிசை 

T = m g = 1.2 × 9.8 = 11.76 N 

ஓரலகு நீளத்திற்கான நிறை μ = 0.25 kg m-1

எனவே, அலைத்துடிப்பின் திசைவேகம் 

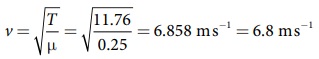
30 செ.மீ தொலைவைக் கடக்க துடிப்பு எடுத்துக் கொள்ளும் நேரம் 

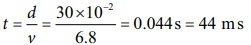
இங்கு, 

ms = மில்லி வினாடி