மீட்சித்தன்மை கொண்ட ஊடகத்தில் நெட்டலையின் திசைவேகம்

இந்த பகுதியில், அலைகளின் திசைவேகத்தை இரு வேறு நிலைகளில் வருவிப்போம்: 

1. நீட்டப்பட்ட கம்பியில் ஏற்படும் குறுக்கலைகளின் திசைவேகம் 

2. மீட்சித்தன்மை கொண்ட ஊடகத்தில் நெட்டலைகளின் திசைவேகம்

மீட்சித்தன்மை கொண்ட ஊடகத்தில் நெட்டலையின் திசைவேகம் 

நீண்ட உருளை வடிவக் குழாயில் குறுக்குவெட்டுப்பரப்பு A, நிலையான நிறை கொண்ட மீட்சித் தன்மை ஊடகம் (இங்கு காற்றைக் கருதுக) P அழுத்தத்தில் உள்ளது என்க. இந்தக் குழாயில் நெட்டலைகளை ஓர் இசைக்கவையை அதிர வைத்தோ, பிஸ்டன் ஒன்றைக் கொண்டு காற்றை அழுத்தியோ ஏற்படுத்தலாம். உருளையின் அச்சுக்கு Δ இணையாக அலை முன்னேறுவதாகக் கொள்க.

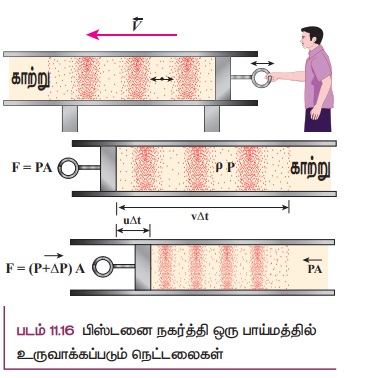
ஆரம்பத்தில் ஓய்வில் உள்ள ஊடகத்தின் அடர்த்தி ρ என்க. t = 0  நேரத்தில் பிஸ்டன் இடது முனையிலிருந்து, u திசைவேகத்துடன் வலது முனைநோக்கி நகர்கிறது.

v என்பது மீட்சி அலையின் திசைவேகம் u மற்றும் பிஸ்டனின் திசைவேகம் என்க. Δt நேர இடைவெளியில் பிஸ்டன் நகரும் தூரம் ∆d = u∆t.  மீட்சித் தன்மை கொண்ட மாறுபாடு நகர்ந்த தொலைவு  ∆x = v∆t. 

Δt நேர இடைவெளியில் v திசைவேகத்தை அடைந்த காற்றின் நிறை ∆m என்க.

∆m = ρ A∆x = ρ A (v ∆t) 

பிஸ்டன் u என்ற திசைவேகத்தில் இயங்குவதால் ஏற்படும் உந்தம்

∆p = [ρ A (v  t)]u.

கணத்தாக்கு என்பது உந்தமாறுபாடு என்பதால், நிகர கணத்தாக்கு

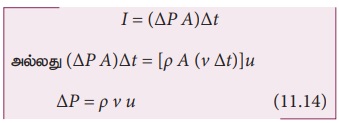
காற்றின் வழியாக, ஒலி அலை செல்லும்போது, சிறிய பருமன் உடைய காற்றுப்பகுதி, தொடர்ந்து இறுக்கங்களுக்கும், தளர்ச்சிகளுக்கும் உட்படுகிறது.

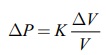
இங்கு, V என்பது காற்றின் தொடக்க பருமன் மற்றும் K என்பது மீட்சி ஊடகத்தின் பருமக்குணகம் (Bulk modulus).

ஆனால் V = A ∆x = A v ∆t and

மேலும் ∆V = A ∆d =A u ∆t

எனவே,

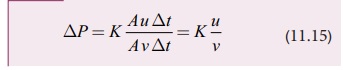
சமன்பாடு (11.14) யும் சமன்பாடு (11.15) யும் ஒப்பிட கிடைப்பது, 

அல்லது

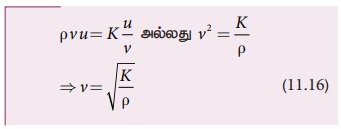
பொதுவாக, மீட்சி ஊடகத்தில் நெட்டலையின் திசைவேகம் v = √E/√P,

இங்கு, E ஊடகத்தின் மீட்சிக்குணகம் (Modulus of elasticity). 

நேர்வுகள்: திண்மத்திற்கு : 

i. ஒரு பரிமாண தண்டு (1 dimensional rod):

இங்கு, Y என்பது தண்டுச் செய்யப்பட்ட பொருளின் யங்குணகம், ρ தண்டின் அடர்த்தி. ஒரு பரிமாண தண்டு யங் குணகத்தை மட்டுமே பெற்றிருக்கும்.

ii. முப்பரிமாண தண்டு (3 dimensional rod): 

திண்மம் ஒன்றின் வழியே நெட்டலையின் வேகம்

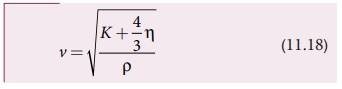
இங்கு, η விறைப்புக்குணகம், B பருமக் குணகம் மற்றும் ρ தண்டின் அடர்த்தி.

நேர்வுகள் : திரவத்திற்கு :

இங்கு K பருமக் குணகம் மற்றும் ρ திரவத்தின் அடர்த்தி. பருமக் குணகம் B அல்லது k என்ற எழுத்தால் குறிப்பிடலாம்.

எடுத்துக்காட்டு 11.7 

எஃகு கம்பி ஒன்றில் ஒலியின் திசைவேகத்தைக் கணக்கிடுக. எஃகின் யங்குணகம் 

Y = 2 × 1011 N m-2 மற்றும் அடர்த்தி ρ = 7800 kg m-3.

தீர்வு: 

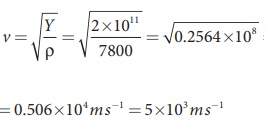
எனவே நெட்டலைகள் திண்மத்தில், திரவம் அல்லது வாயுவை விட வேகமாக செல்கின்றன. ஆடு மேய்ப்பவன் ஆடுகளுடன் தொடர்வண்டி பாதையை கடக்கும் போது, தண்டவாளத்தில் காதை வைத்து கேட்பதன் காரணத்தை தற்போது புரிந்திருப்பீர்கள்.

எடுத்துக்காட்டு 11.8

ஒரு குறிப்பிட்ட பருமன் கொண்ட நீரின் அழுத்தத்தை 100kPa ஆக அதிகரிக்கும்போது பருமன் 0.005% குறைகிறது. 

(a) நீரின் பருமக்குணகம் காண்க? 

(b) நீரில் ஒலியின் (இறுக்கப்பட்ட அலைகள்) திசைவேகத்தைக் காண்க?

தீர்வு

(a) பருமக்குணகம்