யூக்ளிடின் வகுத்தல் துணைத் தேற்றம்

யூக்ளிடின் வகுத்தல் துணைத் தேற்றம் (Euclid's Division Lemma) 

முக்கியக் கணித மேதைகளில் ஒருவராகத் திகழ்ந்த யூக்ளிட் எழுதிய புத்தகமான "எலிமண்ட்ஸ்" 13 தொகுதிகளைக் கொண்டது. முதல் ஆறு தொகுதிகள் வடிவியல் சார்ந்தவை. இதனாலேயே யூக்ளிடை "வடிவியலின் தந்தை" என அழைக்கிறோம். ஆனால், அவர் அடுத்த சில தொகுதிகளில் எண்களின் பண்புகளை அறிந்து கொள்ளப் பல அடிப்படைத் தகவல்களை வழங்கியுள்ளார். அதில் ஒன்றுதான் யூக்ளிடின் வகுத்தல் துணைத் தேற்றம். இது நீங்கள் முந்தைய வகுப்புகளில் செய்த எண்களின் நீள் வகுத்தல் முறையின் சுருக்கமே ஆகும். 

இங்கு நாம் யூக்ளிடின் வகுத்தல் துணைத் தேற்றத்தையும் மற்றும் அதன் பயன்பாடான யூக்ளிடின் வகுத்தல் வழிமுறையையும் கற்க உள்ளோம்.

லெம்மா (lemma) என்பது ஒரு முக்கியத் தேற்றத்தை நிரூபிக்க உதவும் ஒரு துணைத் தேற்றம் ஆகும். இது வழக்கமாக ஒரு சிறு தேற்றம் எனக் கருதப்படும். 

தேற்றம் 1: யூக்ளிடின் வகுத்தல் துணைத் தேற்றம்

a மற்றும் b என்பன ஏதேனும் இரு மிகை முழுக்கள் எனில், a = bq + r, 0 ≤ r < b. என்றவாறு q, r எனும் தனித்த மிகை முழுக்கள் கிடைக்கும்.

குறிப்பு

· வகுத்தலில் கிடைக்கும் மீதியானது வகுக்கும் எண்ணைவிட எப்போதும் சிறியதாகவே அமையும். 

· r = 0 எனில் a = bq. எனவே b ஆனது a ஐ வகுக்கும்.  

· மறுதலையாக b ஆனது a ஐ வகுக்கும் எனில், a = bq

எடுத்துக்காட்டு 2.1 

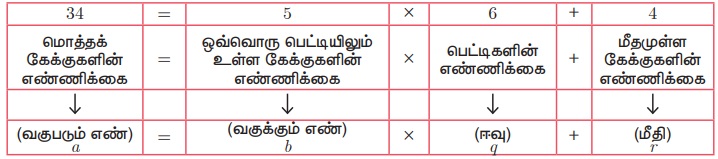
நம்மிடம் 34 கேக் துண்டுகள் உள்ளன. ஒவ்வொரு பெட்டியிலும் 5 கேக்குகள் மட்டுமே வைக்க இயலுமெனில் கேக்குகளை வைக்க எத்தனை பெட்டிகள் தேவை மற்றும் எத்தனை கேக்குகள் மீதமிருக்கும் எனக் காண்க.

தீர்வு 

30 கேக்குகளை வைக்க 6 பெட்டிகள் தேவைப்படுகின்றன. அதில் 4 கேக்குகள் மீதமிருக்கும். கேக்குகளைப் பெட்டிகளில் வைக்கும் இம்முறையைப் பின்வருமாறு புரிந்து கொள்ளலாம். 

குறிப்பு 

· மேற்கண்ட துணைத் தேற்றமானது நீள் வகுத்தல் முறையின் மறுவடிவமே ஆகும். இங்கு q மற்றும் r என்பவை முறையே ஈவு மற்றும் மீதி ஆகும்.

· எந்தவொரு மிகை முழுவையும் 2 ஆல் வகுக்கும் போது 0 அல்லது 1 மட்டுமே மீதியாகக் கிடைக்கும். எனவே, எந்தவொரு மிகை முழுவையும் 2k அல்லது 2k + 1 என்ற வடிவில் எழுதலாம். இங்கு k என்பது ஒரு மிகை முழு.

யூக்ளிடின் வகுத்தல் துணைத் தேற்றத்தை எந்த இரு முழுக்களுக்கும் பொதுமைப்படுத்த இயலும். 

பொதுமைப்படுத்தப்பட்ட யூக்ளிடின் வகுத்தல் துணைத் தேற்றம்

a மற்றும் b (b ≠ 0) என்பன ஏதேனும் இரு முழுக்கள் எனில், a = bq + r, 0 ≤ r < |b| என்றவாறு q, r எனும் முழுக்கள் கிடைக்கும்.

எடுத்துக்காட்டு 2.2 

பின்வரும் ஒவ்வொன்றிலும் a - யை b ஆல் வகுக்கும் போது கிடைக்கும் ஈவு மற்றும் மீதியைக் காண்க. 

(i) a = −12, b = 5 

(ii) a = 17, b = −3 

(iii) a = −19, b = −4 

தீர்வு 

(i) a = −12, b = 5 

யூக்ளிடின் வகுத்தல் துணைத் தேற்றத்தின்படி,

a = bq + r, இங்கு 0 ≤ r < |b|

−12 = 5 × (−3) + 3   0 ≤ r < |5|

எனவே, ஈவு q = -3, மீதி r = 3 

(ii) a = 17, b = −3 

யூக்ளிடின் வகுத்தல் துணைத் தேற்றத்தின்படி,

a = bq + r, இங்கு 0 ≤ r < |b|

17 = (−3) × (−5) + 2 , 0 ≤ r < |-3|

எனவே, ஈவு q  = −5, மீதி r = 2

(iii) a = −19, b = −4 

யூக்ளிடின் வகுத்தல் துணைத் தேற்றத்தின்படி, 

a = bq + r, 0 ≤ r < |b|

−19 = (−4) × (5) + 1, 0 ≤ r < |-4|

எனவே, ஈவு q = 5, மீதி r = 1.

சிந்தனைக் களம் 

ஒரு மிகை முழுவை 3 ஆல் வகுக்கும்போது 

1. கிடைக்கும் மீதிகள் எவை? 

2. அவற்றை எந்த வடிவில் எழுத இயலும்?

முன்னேற்றச் சோதனை

பின்வரும் முழுக்கள் a, b ஆகியவற்றிற்கு a = bq + r என்பதை நிறைவு செய்யும்படி q மற்றும் r காண்க. 

1. a = 13, b = 3 

2. a = 18, b = 4 

3. a = 21, b = -4

4. a = -32, b = -12

5. a = -31, b = 7

எடுத்துக்காட்டு 2.3 

ஒற்றை முழுக்களின் வர்க்கமானது 4q + 1, (இங்கு q ஆனது முழுக்கள்) என்ற வடிவில் அமையும் எனக் காட்டுக. 

தீர்வு 

x என்பது ஓர் ஒற்றை முழுக்கள் என்க. எந்தவொரு ஒற்றை முழுக்களுக்கும் ஏதேனும் ஓர் இரட்டை முழுக்களை விட ஒன்று அதிகமாக இருக்கும் என்பதால், x = 2k + 1, இங்கு k என்பது ஏதேனும் ஒரு முழுக்கள்.

x2 = (2k + 1)2

= 4k2 + 4k + 1

= 4k (k + 1) + 1

= 4q + 1, இங்கு, q = k (k + 1) என்பது முழுக்கள்