தேற்றம், எடுத்துக்காட்டு, தீர்வு | கணக்கு - பெருக்குத்தொடர் வரிசையின் முதல் n உறுப்புகளின் கூடுதல். (பெருக்குத்தொடர் வரிசை) | 10th Mathematics : UNIT 2 : Numbers and Sequences
10வது கணக்கு : அலகு 2 : எண்களும் தொடர்வரிசைகளும்
பெருக்குத்தொடர் வரிசையின் முதல் n உறுப்புகளின் கூடுதல். (பெருக்குத்தொடர் வரிசை)
பெருக்குத்தொடர் வரிசையின் முதல் n உறுப்புகளின் கூடுதல். (Sum to n terms of a G.P.)
ஒரு தொடரிலுள்ள உறுப்புகள் அனைத்தும் பெருக்குத் தொடர்வரிசையில் அமைந்தால் அந்தத் தொடர் பெருக்குத் தொடர் எனப்படும்.
a, ar, ar2, ...arn-1 , ... என்பது ஒரு பெருக்குத் தொடர்வரிசை என்க. பெருக்குத் தொடர்வரிசையின் முதல் n உறுப்புகளின் கூடுதல்.
Sn = a +ar + ar 2 + ... + arn −2 + arn−1 ... (1)
இருபுறமும் r ஆல் பெருக்க நாம் பெறுவது,
rSn = ar +ar2 + ar3 + ... + arn −1 +arn … (2)
(2) − (1) ⇒ rSn − Sn = arn –a
Sn (r −1) = a (rn –1)
ஆகவே ஒரு பெருக்குத் தொடர்வரிசையில் முதல் n உறுப்புகளின் கூடுதல் 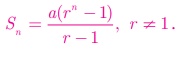
குறிப்பு
r = 1 எனும் போது பெருக்குத் தொடர்வரிசையின் முதல் n உறுப்புகளின் கூடுதலைக் காண மேற்கண்ட சூத்திரத்தைப் பயன்படுத்த முடியாது.
r = 1, எனில்,
Sn = a + a + a + … + a = na
முன்னேற்றச் சோதனை
1. ஒரு தொடரிலுள்ள உறுப்புகள் பெருக்குத் தொடர் வரிசையில் இருக்குமானால் அது ______ எனப்படும்.
2. r = 1 எனும்போது பெருக்குத் தொடர்வரிசையின் முதல் n உறுப்புகளின் கூடுதல் காணும் சூத்திரம் ______.
3. r ≠ 1 எனும்போது பெருக்குத் தொடர்வரிசையின் முதல் n உறுப்புகளின் கூடுதல் காணும் சூத்திரம் ______.
பெருக்குத் தொடர்வரிசையின் முடிவுறா உறுப்புகள் வரை கூடுதல் (Sum to infinite terms of a G.P.)
பெருக்குத் தொடர்வரிசையின் முடிவுறா உறுப்புகள் வரை கூடுதல் S∞ = a + ar +ar 2 + ar 3 +….. = a /(1-r), -1 < r < 1
எடுத்துக்காட்டு 2.46
1, -3, 9, -27... என்ற பெருக்குத் தொடர்வரிசையின் முதல் 8 உறுப்புகளின் கூடுதல் காண்க.
தீர்வு
முதல் உறுப்பு a = 1, பொது விகிதம் r = -3/1 = -3 < 1, n = 8.
பெருக்குத் தொடர்வரிசையின் முதல் n உறுப்புகளின் கூடுதல் 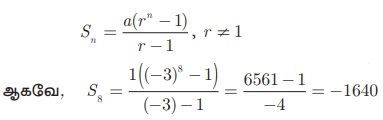
எடுத்துக்காட்டு 2.47
ஒரு பெருக்குத் தொடர்வரிசையில் S6 = 4095 மற்றும் r = 4 எனில், அதன் முதல் உறுப்பைக் காண்க.
தீர்வு
பொது விகிதம் = 4 > 1, முதல் 6 உறுப்புகளின் கூடுதல் S6 = 4095
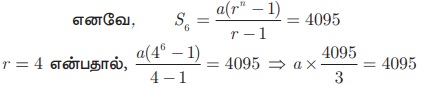
முதல் உறுப்பு a = 3.
எடுத்துக்காட்டு 2.48
1 + 4 + 16 + ... என்ற தொடரின் எத்தனை உறுப்புகளைக் கூட்டினால் கூடுதல் 1365 கிடைக்கும்?
தீர்வு
கூடுதல் 1365 கிடைக்க கூட்ட வேண்டிய உறுப்புகளின் எண்ணிக்கை n என்க.
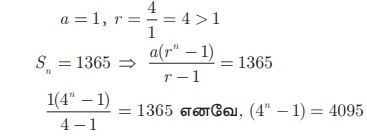
4n = 4096 ⇒ 4n = 46
n = 6
முன்னேற்றச் சோதனை
1. பெருக்குத் தொடர்வரிசையின் முடிவுறா உறுப்புகள் வரை கூடுதல் ______________
2. பெருக்குத் தொடர்வரிசையின் முடிவுறா உறுப்புகள் வரை கூடுதல் காணும் சூத்திரம் r -யின் எம்மதிப்புகளுக்குப் பொருந்தும்?
எடுத்துக்காட்டு 2.49
3 + 1 + 1/3 +..... ∞ என்ற தொடரின் கூடுதல் காண்க.
தீர்வு
இங்கு a = 3, 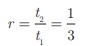
பெருக்குத் தொடர்வரிசையின் முடிவுறா உறுப்புகள் வரை கூடுதல் = 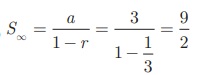
எடுத்துக்காட்டு 2.50
0.6666... என்ற எண்ணின் விகிதமுறு வடிவம் காண்க
தீர்வு
0.6666 ...என்ற எண்ணைப் பின்வருமாறு எழுதலாம்.
0.6666... = 0.6 + 0.06 + 0.006 + 0.0006 + ...
0.6, 0.06, 0.006... என்ற எண்கள் ஒரு பெருக்குத் தொடர்வரிசையை அமைக்கின்றன.
முதல் உறுப்பு a = 0.6, பொது விகிதம் r = 0.06 / 0.6 = 0.1 . மேலும் − 1 < r = 0.1 < 1
பெருக்குத் தொடர்வரிசையின் முடிவுறா உறுப்புகள் வரை கூடுதல் காணும் சூத்திரத்தைப் பயன்படுத்த நாம் பெறுவது,
0.6666... = 0.6 + 0.06 + 0.006 + 0.0006 + ... 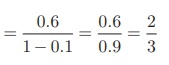
ஆகவே 0.6666... என்ற எண்ணின் விகிதமுறு வடிவம் 2/3 ஆகும்.
செயல்பாடு 5
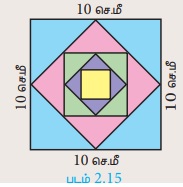
கொடுக்கப்பட்ட சதுரத்தின் பக்கம் 10 செ.மீ. இதன் பக்கங்களின் மையப்புள்ளிகளை இணைத்து ஒரு புதிய சதுரம் உருவாக்கப்படுகிறது. இந்தப் புதிய சதுரத்தின் மையப்புள்ளிகளை இணைத்து மீண்டும் ஒரு சதுரம் உருவாக்கப்படுகிறது. இந்தச் செயல்முறை முடிவில்லாமல் தொடர்கிறது. இந்தச் செயல்முறையில் உருவான சதுரங்களின் பரப்பளவு மற்றும் சுற்றளவுகளின் கூடுதல் காண்க.
எடுத்துக்காட்டு 2.51
5 + 55 + 555 + ... என்ற தொடர்வரிசையின் முதல் n உறுப்புகளின் கூடுதல் காண்க.
தீர்வு
5 + 55 + 555 + ... என்பது ஒரு கூட்டுத் தொடர்வரிசையும் அல்ல, பெருக்குத் தொடர்வரிசையும் அல்ல. எனவே, இந்தத் தொடரை இரு தொடர்களாகப் பிரித்துக் கூடுதல் காண்போம்.
5 + 55 + 555 + ... n உறுப்புகள் வரை = 5 [1 + 11 + 111 + ... n உறுப்புகள் வரை]
= 5/9 [9 + 99 + 999 + ... n உறுப்புகள் வரை]
= 5/9 [(10 – 1) + (100 – 1) + (1000 - 1) + … n உறுப்புகள் வரை]
= 5/9 [(10 + 100 + 1000 + ... n உறுப்புகள் வரை] - n]
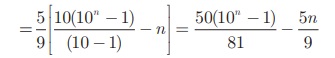
முன்னேற்றச் சோதனை
1. 3 + 33 + 333 + ... என்பது ஒரு பெருக்குத் தொடரா?
2.1 + r + r2 + r3... = 3/4 என்றவாறு அமையும் r-யின் மதிப்பு ___.
எடுத்துக்காட்டு 2.52
1 + 6 + 62 + ... + 6n > 5000 என்றவாறு அமையும் மிகச் சிறிய மிகைமுழு எண் n காண்க.
தீர்வு
எத்தனை குறைவான உறுப்புகளைக் கூட்டினால் கூடுதல் 5000-ஐத் தாண்டும் என நாம் காண வேண்டும்.
அதாவது எந்தக் குறைவான n மதிப்பிற்கு Sn > 5000 வரும் எனக் காண வேண்டும்.
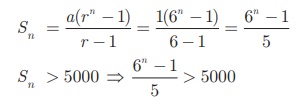
6n -1 > 25000 ⇒ 6n > 25001
65 = 7776 மற்றும் 66 =46656 என்பதால்
1 + 6 + 62 + ... + 6n > 5000 என்றவாறு அமையும் மிகச்சிறிய n -ன் மதிப்பு 6 ஆகும்.
எடுத்துக்காட்டு 2.53
ஒரு நபர் ஒவ்வோர் ஆண்டும் அதற்கு முந்தைய ஆண்டு சேமித்த தொகையில் பாதியைச் சேமிக்கிறார். 6 ஆண்டுகளில் அவர் ₹7875-ஐச் சேமிக்கிறார் எனில், முதல் ஆண்டில் அவர் சேமித்த தொகை எவ்வளவு?
தீர்வு
6 ஆண்டுகளில் அவர் சேமித்த தொகை S6 = 7875
ஒவ்வோர் ஆண்டும் சேமிக்கும் தொகையானது அதற்கு முந்தைய ஆண்டின் சேமிப்புத் தொகையில் பாதி என்பதால், r = 1/2 < 1
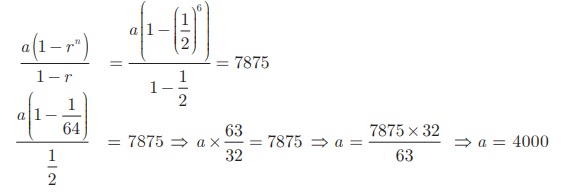
எனவே, அந்த நபர் முதல் ஆண்டில் சேமித்த தொகை ₹ 4000.