மட்டு எண்கணிதம்

மட்டு எண்கணிதம் (Modular Arithmetic)

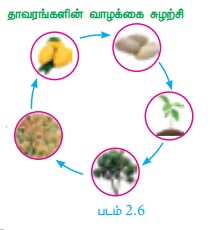
கடிகாரத்தில் 24 மணி நேரத்தைக் குறிக்க நாம் 1 முதல் 12 வரை உள்ள எண்களைப் பயன்படுத்துகிறோம். ஒரு நாளின் 24 மணி நேரத்தை எவ்வாறு ஒரு 12 மணி நேர எண் அமைப்பில் குறிக்க இயலும்? நாம் 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 மற்றும் 12 க்கு பிறகு மீண்டும் 1, 2, 3,... எனத் தொடங்குகிறோம். இந்த அமைப்பில் நேரமானது 1 முதல் 12 வரை சுழன்று கொண்டே உள்ளன. இது போல ஒரு குறிப்பிட்ட மதிப்பை அடைந்தவுடன் மீண்டும் ஒரே எண்களைத் தொடர்ந்து பெறுவது மட்டு எண்கணிதம் ஆகும். 

கணிதத்தில் மட்டு எண்கணிதம் என்பது ஒரு குறிப்பிட்ட எண்ணைச் சுற்றி மீண்டும் இடம் பெறும் முழுக்களின் அமைப்பு ஆகும். இயல்பான எண்கணிதம் போன்றில்லாமல் மட்டு எண் கணிதம் சுழற்சி அடிப்படையில் செயல்படுகிறது. 'மட்டு எண்கணிதம்' என்ற கருத்தை உருவாக்கியவர் மாபெரும் ஜெர்மானியக் கணித மேதை கார்ல் பிரடெரிக் காஸ் ஆவார். இவர் "கணித மேதைகளின் இளவரசர்” என அழைக்கப்படுகிறார். 

உதாரணங்கள் 

1. பகல் மற்றும் இரவு தொடர்ந்து மாறிக்கொண்டே இருக்கும். 

2. ஒரு வாரத்தின் நாட்கள் ஞாயிறு முதல் சனி வரை தொடர்ச்சியாக மாறிக் கொண்டே இருக்கும். 

3. தாவரங்களின் வளர்ச்சி மாற்றம். 

4. ஒரு வருடத்தின் காலநிலை தொடர்ந்து மாறிக்கொண்டே இருக்கும் (கோடைக்காலம், மழைக்காலம், குளிர்காலம், வசந்தகாலம்) 

5. இரயில்வே மற்றும் விமான நேரங்கள் 24 மணி நேரச் சுழற்சி அடிப்படையில் உள்ளன. இரயில்வே நேரம் 00.00-யில் தொடங்குகிறது. 23:59 -ஐ அடைந்தவுடன், அடுத்த நிமிடம் 24:00 என்பதற்குப் பதிலாக 00:00 என மாறுகிறது. 

1. மட்டு ஒருங்கிசைவு (Congruence Modulo)

a மற்றும் b - க்கு இடையே உள்ள வித்தியாசம் n -யின் மடங்கு எனில் மட்டு n -யின் அடிப்படையில் a யும் b யும் ஒருங்கிசைவு உடையதாகும். அதாவது a - b = kn k ∈ ℤ. இதை a ≡ b (மட்டு n) எனவும் எழுதலாம். 

இங்கு n என்பது மட்டு எண் என அழைக்கப்படுகிறது. வேறு விதமாகச் சொல்வோமேயானால் a ≡ b (மட்டு n) என்பதன் பொருள் a - b ஆனது n ஆல் வகுபடும் எனலாம்.

எடுத்துக்காட்டாக, 61 ≡ 5 (மட்டு 7) ஏனெனில், 61 - 5 = 56 என்பது 7 ஆல் வகுபடும்.

குறிப்பு

• ஒரு மிகை முழுவை n ஆல் வகுக்கும்போது கிடைக்கும் மீதிகள் 0, 1, 2, …, n - 1 ஆகும். 

• எனவே மட்டு n ஐ கணக்கிடும் போது, நாம் அனைத்து எண்களையும் n ஆல் வகுத்துக் கிடைக்கும் மீதிகளான 0,1,2,3,..., n - 1 ஆல் பதிலிட வேண்டும்.

மட்டு ஒருங்கிசைவை தெளிவாகப் புரிந்து கொள்வதற்காக மேலும் இரு விளக்கங்களைக் காண்போம். 

விளக்கம் 1

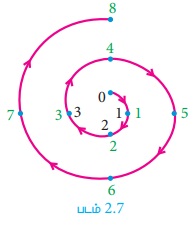
8 (மட்டு 4) காண்க 

மட்டு 4 காண்பதற்கு (சாத்தியமான மீதிகள் 0, 1, 2, 3 என்பதால்) 0,1,2,3 என்ற எண்களைக் கொண்டு கடிகாரம் போன்ற அமைப்பை உருவாக்குவோம். பூச்சியத்தில் தொடங்கிக் கடிகார முள்ளின் திசையில் 8 எண்கள் 1, 2, 3, 0, 1, 2, 3, 0 என்றவாறு நகர வேண்டும். 8 எண்கள் சுழற்சியாக நகர்ந்த பிறகு நாம் 0 என்ற எண்ணில் முடிக்கிறோம். 

எனவே, 8 ≡ 0 (மட்டு 4)

விளக்கம் 2

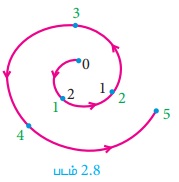
-5 (மட்டு 3) காண்க 

மட்டு 3 காண்பதற்கு (சாத்தியமான மீதிகள் 0, 1, 2 என்பதால்) 0, 1, 2 என்ற எண்களைக் கொண்டு கடிகாரம் போன்ற அமைப்பை உருவாக்குவோம். குறை எண் என்பதால் பூச்சியத்தில் தொடங்கிக் கடிகார முள்ளின் எதிர்திசையில் 5 எண்கள் 2, 1, 0, 2, 1 என்றவாறு நகர வேண்டும். 5 எண்கள் கடிகார முள்ளின் எதிர்திசையில் சுழற்சியாக நகர்ந்த பிறகு நாம் 1 என்ற எண்ணில் முடிக்கிறோம். எனவே, - 5 ≡ 1 (மட்டு 3)

2. யூக்ளிடின் வகுத்தல் துணைத் தேற்றத்தை மட்டு எண் கணிதத்துடன் தொடர்புபடுத்துதல் (Connecting Euclid's Division lemma and Modular Arithmetic)

m மற்றும் n என்பன இரு முழுக்கள் மற்றும் m ஒரு மிகை முழு என்க. யூக்ளிடின் வகுத்தல் துணைத் தேற்றத்தின்படி n = mq + r இங்கு 0 ≤ r  < m மற்றும் q ஒரு முழு என நாம் எழுதலாம். n = mq + r என ஒவ்வொரு முறையும் எழுதுவதற்குப் பதிலாக, நாம் மட்டு ஒருங்கிசைவுக் குறியீட்டைப் பயன்படுத்திப் பின்வருமாறு எழுதலாம். 

n = mq + r q ஒரு முழு எனில் n ஆனது மட்டு m-ஐப் பொறுத்து r உடன் ஒருங்கிசைவாக உள்ளது என நாம் கூறலாம்.

n = mq + r

n–r = mq

n–r ≡ 0 (மட்டு m) 

n ≡ r (மட்டு m)

ஆகவே யூக்ளிடின் வகுத்தல் துணைத் தேற்றத்தின் மூலம் பெறப்பட்ட n = mq + r என்ற சமன்பாட்டை n ≡ r (மட்டு m) என்ற மட்டு ஒருங்கிசைவாக எழுதலாம். 

முன்னேற்றச் சோதனை

1. _________________ எனில் மட்டு n அடிப்படையில் a-யும் b-யும் ஒருங்கிசைவு உடையதாகும். 

2. 7 ஆல் வகுக்கும் போது மீதி 5 தரக்கூடிய அனைத்து மிகை முழுக்களின் கணம் _______________.

குறிப்பு 

a மற்றும் b என்ற இரு முழுக்களும் மட்டு m ஐப் பொறுத்து ஒருங்கிசைவாக அமைய, அதாவது a ≡ b (மட்டு m), என எழுத வேண்டுமானால் அவ்விரு எண்களையும் m ஆல் வகுக்கும் போது ஒரே மீதியைத் தர வேண்டும்.

சிந்தனைக் களம்

3 ஆல் வகுக்கும்போது மீதி 2 கிடைக்கக்கூடிய வகையில் எத்தனை முழுக்கள் இருக்கும்?

3. மட்டு எண்கணிதச் செயல்பாடுகள் (Modulo operations)

எண்கள் மீதான அடிப்படைச் செயல்பாடுகளான கூட்டல், கழித்தல் மற்றும் பெருக்கல் போன்று மட்டு எண்கணிதத்திலும் அதே செயல்பாடுகளை நாம் செய்யலாம். இச்செயல்பாடுகளைச் செய்வதற்குத் தேவையான கருத்துகளைப் பின்வரும் தேற்றம் வழங்குகிறது. 

தேற்றம் 5

a, b, c மற்றும் d என்பன முழுக்கள் மற்றும் m என்பது ஒரு மிகை முழு. a ≡ b (மட்டு m) மற்றும் c ≡ d (மட்டு m) எனில்,

(i) (a + c) ≡ (b + d) (மட்டு m)

(ii) (a − c) ≡ (b − d) (மட்டு m)

(iii) (a ×c) ≡ (b ×d) (மட்டு m)

விளக்கம் 3

17 ≡ 4 (மட்டு 13) மற்றும் 42 ≡ 3 (மட்டு 13) எனில், தேற்றம் 5-ன் படி, (i) 17 + 42 ≡ 4 + 3 (மட்டு 13)

59 ≡ 7 (மட்டு 13)

(ii) 17 - 42 ≡ 4 - 3 (மட்டு 13)

-25 ≡ 1 (மட்டு 13)

(iii) 17 × 42 ≡ 4 × 3 (மட்டு 13)

714 ≡ 12 (மட்டு 13) 

தேற்றம் 6 

a ≡ b (மட்டு m) எனில், 

(i) ac ≡ bc (மட்டு m)

(ii)  a ± c ≡ b ± c (மட்டு m)

இங்கு c என்பது ஏதேனும் ஒரு முழுக்கள் 

முன்னேற்றச் சோதனை

1. (k-3) ≡ 5 (மட்டு11) என்றவாறு அமையும் k என்ற மிகை எண்கள் ____.

2. 59 ≡ 3 (மட்டு 7), 46 ≡ 4 (மட்டு 7) எனில், 105 ≡ ____ (மட்டு 7), 13 ≡ ____ (மட்டு 7), 413 ≡ _____ (மட்டு 7), 368 ≡ ____ (மட்டு 7). 

3. 7 × 13 × 19 × 23 × 29 × 31 என்ற எண்ணை 6 ஆல் வகுக்கக் கிடைக்கும் மீதி ____.

எடுத்துக்காட்டு 2.11 

70004 மற்றும் 778 ஆகிய எண்களை 7 ஆல் வகுக்கக் கிடைக்கும் மீதியைக் காண்க. 

தீர்வு 

70000 ஆனது 7 ஆல் வகுபடும் என்பதால்

70000 ≡ 0 (மட்டு 7) 

70000 + 4 ≡ 0 + 4 (மட்டு 7)

70004 ≡ 4 (மட்டு 7)

எனவே 70004 ஐ 7 ஆல் வகுக்கக் கிடைக்கும் மீதி 4. 

777 ஆனது 7 ஆல் வகுபடும் என்பதால்

777 ≡ 0 (மட்டு 7) 

777 + 1 ≡ 0 + 1 (மட்டு 7)

778 ≡ 1 (மட்டு 7)

எனவே, 778 ஐ 7 ஆல் வகுக்கக் கிடைக்கும் மீதி 1.

எடுத்துக்காட்டு 2.12 

15 ≡ 3 (மட்டு d) என்றவாறு அமையும் d -யின் மதிப்பைத் தீர்மானிக்க. 

தீர்வு 

15 ≡ 3 (மட்டு d) என்பதன் பொருள் 15 – 3 = kd, இங்கு k என்பது ஏதேனும் ஒரு முழுக்கள்.

12 = kd. 

d ஆனது 12 ஐ வகுக்கும்.

12 -யின் வகுத்திகளாவன 1,2,3,4,6,12.

d ஆனது 3 ஐ விட அதிகமாக இருக்க வேண்டும், ஏனெனில் மீதி 3 வந்துள்ளது. எனவே, d - க்கு சாதகமான மதிப்புகள் 4,6,12 ஆகும்.

எடுத்துக்காட்டு 2.13 

பின்வருவனவற்றிற்குப் பொருந்தக்கூடிய குறைந்தபட்ச மிகை x-ஐக் காண்க. 

(i) 67 + x ≡ 1 (மட்டு 4) 

(ii) 98 ≡ (x + 4) (மட்டு 5) 

தீர்வு 

(i) 67 + x ≡ 1 (மட்டு 4)

67 + x – 1 = 4n, இங்கு n என்பது ஏதேனும் ஒரு முழுக்கள்

66 + x = 4n

66 + x என்பது 4 -யின் மடங்கு. 

66 ஐ விட அதிகமான 4 - யின் மடங்கு 68. எனவே x-யின் குறைந்தபட்ச மதிப்பு 2 ஆகும். 

(ii) 98 ≡ (x + 4) (மட்டு 5)

98 − (x + 4) = 5n, n என்பது ஏதேனும் ஒரு முழுக்கள்

94 - x = 5n

94 – x என்பது 5 -யின் மடங்கு 

94 ஐ விடக் குறைவான 5 -யின் மடங்கு 90. எனவே x-யின் குறைந்தபட்ச மதிப்பு 4 ஆகும்.

குறிப்பு 

இயற்கணிதத்தில் பல்லுறுப்புக் கோவைச் சமன்பாடுகளைத் தீர்க்கும் போது பெரும்பாலும் நமக்கு முடிவுறு எண்ணிக்கையிலான தீர்வுகள் கிடைக்கும். ஆனால், மட்டு ஒருங்கிசைவு சமன்பாடுகளைத் தீர்க்கும்போது நமக்கு எண்ணற்றத் தீர்வுகள் கிடைக்கும்.

எடுத்துக்காட்டு 2.14 

தீர்க்க 8x ≡ 1 (மட்டு 11) 

தீர்வு 

8x ≡ 1 (மட்டு 11) என்பதை 8x - 1 = 11k, இங்கு k என்பது ஏதேனும் ஒரு முழுக்கள், என எழுதலாம்.

x = (11k + 1) / 8 

k = 5, 13, 21, 29,.... என நாம் பிரதியிடும் போது 11k + 1 ஆனது 8 ஆல் வகுபடுகிறது.

x = (11 × 5 + 1) /8 =  7

x = (11 × 13 + 1) /8 = 18

⸫ 7,18,29,40, ... என்பது தீர்வாகும்.

எடுத்துக்காட்டு 2.15 

104 ≡ x (மட்டு 19) என்றவாறு அமையும் x மதிப்பைக் கணக்கிடுக. 

தீர்வு 

102 = 100 ≡ 5 (மட்டு 19)

104 = (102)2 ≡ 52 (மட்டு 19)

104 ≡ 25 (மட்டு 19)

104 ≡ 6 (மட்டு 19) (ஏனெனில், 25 ≡ 6 (மட்டு 19)) 

எனவே, x = 6. 

எடுத்துக்காட்டு 2.16 

3x ≡ 1 (மட்டு 15) என்ற சமன்பாட்டிற்கு எத்தனை முழு எண் தீர்வுகள் உள்ளன எனக் காண்க.

தீர்வு 

3x ≡ 1 (மட்டு 15) என்பதை

3x - 1 = 15k, k என்பது ஏதேனும் ஒரு முழு என எழுதலாம். 

3x = 15k + 1

x = [15k + 1] / 3

x = 5k + 1/3

5k என்பது ஒரு முழு எண் என்பதால், 5k + (1/3) என்பது ஒரு முழு எண் அல்ல. எனவே இச்சமன்பாட்டிற்கு முழு எண் தீர்வே இல்லை. 

எடுத்துக்காட்டு 2.17 

ஒருவர் சென்னையிலிருந்து டெல்லிக்குச் செல்ல இரயிலில் புறப்படுகிறார். அவர் தனது பயணத்தைப் புதன்கிழமை 22.30 மணிக்குத் தொடங்குகிறார். எந்தவிதத் தாமதமுமின்றி இரயில் செல்வதாகக் கொண்டால் மொத்தப் பயண நேரம் 32 மணி நேரம் ஆகும். அவர் எப்பொழுது டெல்லியைச் சென்றடைவார்? 

தீர்வு 

பயணம் தொடங்கும் நேரம் 22.30. பயண நேரம் 32 மணி நேரம் இங்கு நாம் மட்டு 24 ஐ பயன்படுத்த உள்ளோம். 

சென்று சேரும் நேரம் 

22.30 + 32 (மட்டு 24) ≡ 54.30 (மட்டு 24) 

≡ 6.30 (மட்டு 24) (அதாவது 32 = (1 × 24) + 8 வியாழன் வெள்ளி) 

ஆகவே அவர் வெள்ளிக்கிழமை காலை 6.30 மணிக்கு டெல்லி சென்றடைவார்.

எடுத்துக்காட்டு 2.18 

கலா மற்றும் வாணி இருவரும் நண்பர்கள். "இன்று எனது பிறந்தநாள்" எனக் கலா கூறினாள். வாணியிடம், "உனது பிறந்தநாளை எப்போது நீ கொண்டாடினாய்?" எனக் கேட்டாள். அதற்கு வாணி இன்று திங்கள்கிழமை, நான் என்னுடைய பிறந்த நாளை 75 நாட்களுக்கு முன் கொண்டாடினேன்", எனப் பதிலளித்தாள். வாணியின் பிறந்தநாள் எந்தக் கிழமையில் வந்திருக்கும் எனக் காண்க.

தீர்வு 

நாம் இங்கு ஒவ்வொரு வார நாளுக்கும் ஓர் எண்ணைப் பின்வருமாறு எடுத்துக் கொள்வோம். 0, 1, 2, 3, 4, 5, 6 என்பன முறையே ஞாயிறு முதல் சனி வரை உள்ள கிழமைகளைக் குறிப்பதாக எடுத்துக் கொள்வோம்.

வாணி இன்று திங்கள் கிழமை என்று கூறியதால், அதற்கான எண் 1. வாணியின் பிறந்தநாள் 75 நாட்களுக்கு முன் வருவதால் நாம் 1 -லிருந்து 75 ஐக் கழித்து மட்டு 7 காண வேண்டும், ஏனெனில் 1 வாரத்திற்கு 7 நாட்கள். 

-74 (மட்டு 7)  ≡ -4 (மட்டு 7) ≡ 7 - 4 (மட்டு 7) ≡ 3 (மட்டு 7)

(ஏனெனில், -74 – 3 = -77 ஆனது 7 ஆல் வகுபடும்) 

எனவே, 1 – 75 ≡ 3 (மட்டு 7) 

3 என்ற எண் புதன்கிழமையைக் குறிக்கும். 

எனவே, வாணி தனது பிறந்தநாளைப் புதன்கிழமை கொண்டாடியிருப்பாள்.