வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் - ஒரு கோடும் ஒரு தளமும் சந்திக்கும் புள்ளி (Meeting Point of a Line and a Plane) | 12th Maths : UNIT 6 : Applications of Vector Algebra

12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்

ஒரு கோடும் ஒரு தளமும் சந்திக்கும் புள்ளி (Meeting Point of a Line and a Plane)

தேற்றம் 6.23

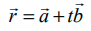என்ற கோடும் 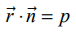என்ற தளமும் சந்திக்கும் புள்ளியின் நிலைவெக்டர்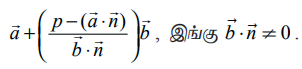

நிரூபணம்

கொடுக்கப்பட்ட 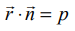என்ற தளத்திற்கு இணையாக இல்லாத கொடுக்கப்பட்ட கோட்டின் சமன்பாடு 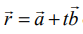என்க. ஆகவே,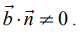

தளத்தை நேர்க்கோடு சந்திக்கும் புள்ளியின் நிலைவெக்டர் என்க. எனவே, t−ன் ஒரு சில மதிப்புகளுக்கு, அதாவது t1 என்ற மதிப்புக்கு 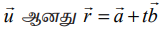என்ற கோட்டின் சமன்பாடு மற்றும் 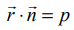என்ற தளத்தின் சமன்பாடு இரண்டையும் நிறைவு செய்யும். ஆதலால்,

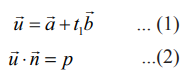
சமன்பாடு (1)−ஐ (2)−ல்பிரதியிட, நாம் பெறுவது

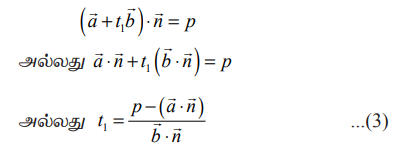
சமன்பாடு (3)−ஐ (1)−ல் பிரதியிட, நாம்பெறுவது

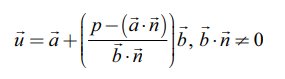
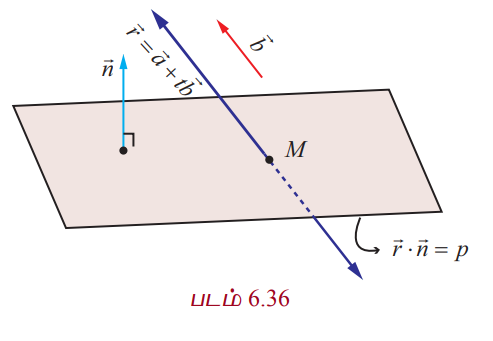
எடுத்துக்காட்டு 6.56

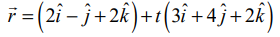என்ற கோடு x−y+z−5=0 என்ற தளத்தை சந்திக்கும் புள்ளியின் ஆய அச்சுத் தூரங்களைக் காண்க.

தீர்வு

அதாவது, கொடுக்கப்பட்ட நேர்க்கோடு தளத்தை சந்திக்கும் புள்ளி (2,−1,2) ஆகும்.

மாற்று முறை

கொடுக்கப்பட்ட நேர்க்கோட்டின் கார்மசியன் சமன்பாடு (x−2)/3 = (y+1)/4 = (z−2)/2 = t (என்க)

இக்கோட்டின் மீதுள்ள ஏதேனும் ஒரு புள்ளியின் அமைப்பு (3t+2,4t−1,2t+2) ஆகும். கொடுக்கப்பட்ட கோடும் தளமும் வெட்டிக்கொள்ளும் எனில், இப்புள்ளி x−y+z−5=0 என்ற தளத்தின் மீது அமையும்.

ஆதலால், (3t+2)−(4t−1)+(2t+2)−5=0=t=0. எனவே, கொடுக்கப்பட்ட கோடு. கொடுக்கப்பட்ட தளத்தை (2,−1,2) என்ற புள்ளியில் சந்திக்கிறது.

Tags : Definition, Theorem, Proof, Solved Example Problems, Solution வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள்.

12th Maths : UNIT 6 : Applications of Vector Algebra : Meeting Point of a Line and a Plane Definition, Theorem, Proof, Solved Example Problems, Solution in Tamil : 12th Standard TN Tamil Medium School Samacheer Book Back Questions and answers, Important Question with Answer. 12 ஆம் வகுப்பு கணிதம் : அத்தியாயம் 6 : வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் : ஒரு கோடும் ஒரு தளமும் சந்திக்கும் புள்ளி (Meeting Point of a Line and a Plane) - வரையறை, தேற்றம், நிரூபணம், எடுத்துக்காட்டு கணக்குகள் : 12 ஆம் வகுப்பு தமிழ்நாடு பள்ளி சமசீர் புத்தகம் கேள்விகள் மற்றும் பதில்கள்.