வெட்டும் கோடுகளால் அமையும் கோண இணைகள்

வெட்டும் கோடுகளால் அமையும் கோண இணைகள்

இப்பகுதியில், அடுத்துள்ள கோணங்கள், நேரிய கோண இணைகள், குத்தெதிர்க் கோணங்கள் போன்ற தொடர்புடைய கோணங்களைப் பற்றி கற்போம். 

1. அடுத்துள்ள கோணங்கள்

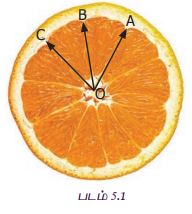
ஆசிரியர், ஒரு ஆரஞ்சுப் பழத்தை வெட்டி அதன்மேல் கோணங்கள் குறித்து காட்டுகிறார். ஆசிரியர் - மாணவர்களுக்கிடையேயான உரையாடலை உற்று நோக்குக. 

ஆசிரியர் : படத்தில் எத்தனை கோணங்கள் குறிக்கப்பட்டுள்ளன? அவற்றின்  பெயர்களைக் கூற இயலுமா? 

கவின் : படத்தில் மூன்று கோணங்கள் குறிக்கப்பட்டுள்ளன. அவை ∠AOC, ∠AOB மற்றும் ∠BOC ஆகும்.

ஆசிரியர் : எந்தெந்தக் கோணங்கள் அடுத்தடுத்து அமைந்துள்ளன? 

தூரிகை : ∠AOB , ∠BOC ஆகிய கோணங்கள் அடுத்தடுத்து  அமைந்துள்ளன. 

ஆசிரியர் : எத்தனை முனைகள் உள்ளன? 

முகில் : ஒரேயொரு பொதுவான முனை உள்ளது. 

ஆசிரியர் : எத்தனை கதிர்கள் உள்ளன? அவற்றிற்குப் பெயரிடுக. 

அமுதன் : மூன்று கதிர்கள் உள்ளன. அவைகள்     மற்றும்   ஆகும். 

ஆசிரியர் : ∠AOB, ∠BOC ஆகிய கோணங்களுக்குப் பொதுவான கதிர் உள்ளதா?

ஓவியா : ஆமாம். என்ற பொதுவான கதிர், ∠AOB, ∠BOC ஆகிய கோணங்களுக்குப் பொதுவாக அமைந்துள்ளது. 

ஆசிரியர் : , ஆகிய கதிர்களைப் பற்றி என்ன கூற இயலும்? 

கவின் : அவை என்ற பொதுவான கதிரின் இருபுறமும் அமைந்துள்ளன. 

ஆசிரியர் : ∠AOB, ∠BOC ஆகிய கோணங்களுக்குப் பொதுவான உட்பகுதிகள் உள்ளதா? 

முகில் : இல்லை . ∠AOB, ∠BOC ஆகியவற்றிற்குப் பொதுவான உட்பகுதிகள் இல்லை . 

ஆசிரியர் : எனவே, ∠AOB மற்றும் ∠BOC ஆகிய இரு கோணங்களுக்கு ஒரு பொதுவான முனை (O), ஒரு பொதுவான கதிர் () உள்ளன. மற்ற இரு கதிர்கள் () மற்றும் ( )  பொதுவான கதிருக்கு இருபுறமும் அமைந்துள்ளன. மேலும் அவற்றிற்குப் பொதுவான உட்பகுதிகள் இல்லை என நாம் கூற இயலும். இவ்வாறு அமைந்த கோணங்கள் ∠AOB மற்றும் ∠BOC ஆகியவை அடுத்தடுத்த கோணங்கள் என்று அழைக்கப்படும்.

எனவே, பொதுவான ஒரு முனை, பொதுவான ஒரு கதிர், மேலும் பொதுவான உட்பகுதி இல்லாத இரு கோணங்கள் அடுத்தடுத்த கோணங்கள் எனப்படும்.

இப்பொழுது அருகிலுள்ள படத்தை (படம் 5.2) உற்று நோக்கவும். அதில் ∠1, ∠2, ∠3 ஆகிய கோணங்கள் குறிக்கப்பட்டு உள்ளன.

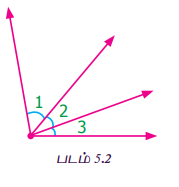
இங்கு ∠1, ∠2 மற்றும் ∠2, ∠3 ஆகிய இரு சோடி அடுத்துள்ள கோணங்கள் அமைந்துள்ளதைக் காணலாம். இப்போது ∠1 மற்றும் ∠3 என்ற சோடிக் கோணங்கள் எந்த வகையைச் சேர்ந்தவை?

அவை அடுத்தமையாக் கோணங்கள் ஏனெனில், இந்தச் சோடி கோணங்களுக்குப், பொதுவாக ஒரு முனை இருந்தாலும், பொதுவாக ஒரு கதிர் இல்லை . மேலும் ∠1 மற்றும் ∠3 ஆகியவற்றிற்குப் பொதுவான உட்பகுதிகளும் இல்லை . மூன்று கட்டுப்பாடுகளையும் நிறைவு செய்யாத காரணத்தால் இந்தக் கோண இணைகள் அடுத்துள்ள கோணங்களாக அமையவில்லை.

சிந்திக்க

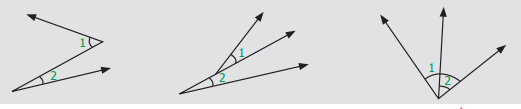
கீழ்வரும் ஒவ்வொரு படத்திலும், ∠1 மற்றும் ∠2 ஆகிய கோணங்கள் குறிக்கப்பட்டுள்ளதைக் காணலாம். அவைகள் அடுத்துள்ள கோணங்களாக அமையுமா? விடைக்குத் தகுந்த காரணம் கூறுக.

இவற்றை முயல்க 

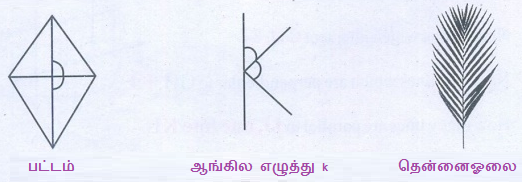
1. அன்றாட வாழ்வில் அடுத்துள்ள கோணங்கள் அமையும் சில எடுத்துக்காட்டுகள் கீழே கொடுக்கப்பட்டுள்ளன.

மேற்குறிப்பிட்டவை தவிர மேலும் மூன்று எடுத்துக்காட்டுகளைக் கூற முடியுமா?

2. படத்தில் குறிக்கப்பட்டுள்ள ஆறு கோணங்களைக் கவனிக்க. ஏதேனும் நான்கு அடுத்துள்ள கோணங்கள் மற்றும் நான்கு அடுத்தமையாக் கோணங்களை எழுதுக.

அடுத்துள்ள கோணங்கள்  ∠A and ∠B, ∠B and ∠C

∠C and ∠D, ∠D and ∠E

∠E and ∠F

அடுத்தமையாக் கோணங்கள் 

∠Aand ∠C

∠B and ∠D

∠C and ∠E

∠Dand ∠F

∠Aand ∠D

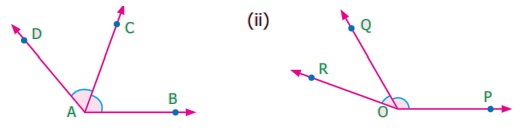
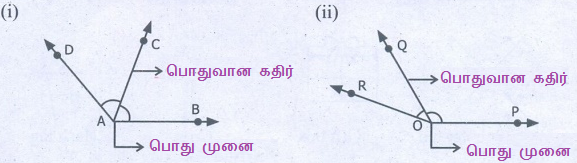
3. கொடுக்கப்பட்டுள்ள ஒவ்வொரு படத்திலும் உள்ள அடுத்துள்ள கோணங்களின் பொதுவான கதிர், பொது முனை ஆகியவற்றைக் கண்டறிக, மேலும் கோண உட்பகுதிகளை இரண்டு வண்ணங்களைப் பயன்படுத்தி நிழலிட்டுக் காட்டுக.

4. 4. கீழ்க்காணும் ஒவ்வொரு படத்திலும் அடுத்துள்ள கோணங்களை எழுதுக.

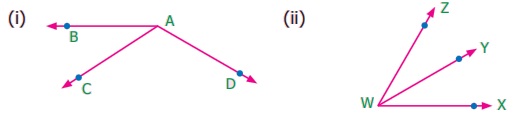
(i) ∠BAC and ∠CAD

(ii) ∠ZWY and ∠YWX

2. நேரிய கோண இணை

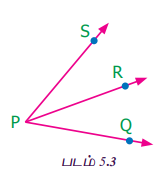
படம் 5.3 இல், ∠QPR மற்றும் ∠RPS ஆகிய அடுத்துள்ள கோணங்களைக் காணலாம்.  ∠QPR-ம் ∠RPS-ம் இணைந்து ∠QPS என்ற குறுங்கோணத்தை உருவாக்குகின்றன என்பது தெளிவு. ∠QPR மற்றும் ∠RPS ஆகியவை அதிகரிக்கும்போது ∠QPS ஆனது (i) செங்கோணம்  (ii) விரிகோணம் (iii) நேர்க்கோணம் மற்றும் (iv) பின்வளைக் கோணம் என மாற்றமடையும் (படம் 5.4 இல் உள்ளவாறு).

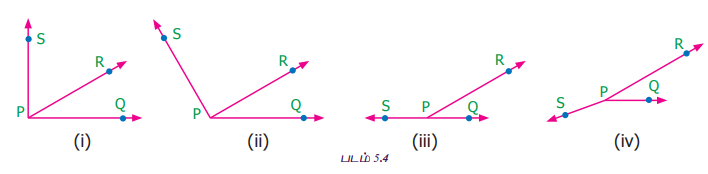
அவ்வாறு உருவான கோணம் ஒரு நேர்கோணமாக அமைந்தால் அவை மிகை நிரப்பு கோணங்கள் என அழைக்கப்படும். மிகை நிரப்பு கோணங்களாக அமையும் அடுத்துள்ள கோணங்கள், நேர்கோட்டின் மீது அமையும் கோண இணைகளை அறிய உதவுகிறது (படம் 5.4 (iii)). இந்தக் கோண இணைகள் நேரிய கோண இணைகள் எனப்படும்.

இவற்றை முயல்க

பின்வரும் படங்களைக் கவனித்து, நேரிய கோண இணையின் மற்றொரு கோணத்தைக் காண்க.

மற்றொரு கோணம்

(i) 96° (ii) 94° (iii) 21o

சிந்திக்க

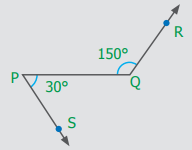
படத்தை நன்கு கவனிக்க. ∠PQR = 150° மற்றும் ∠QPS = 30° ஆகிய இரு கோணங்கள் உள்ளன. அனைத்து மிகை நிரப்பு கோணங்களும் நேரிய கோண இணை ஆகுமா? கலந்துரையாடுக.

எடுத்துக்காட்டு 5.1 

கொடுக்கப்பட்டுள்ள படம் 5.5-ல், ∠AOC -ஐக் காண்க.

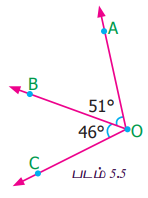
தீர்வு 

∠AOC = ∠AOB + ∠BOC

= 46° + 51o 

= 97°

எடுத்துக்காட்டு 5.2 

∠POQ = 23° மற்றும் ∠POR = 62° எனில், ∠QOR ஐக் காண்க 

தீர்வு

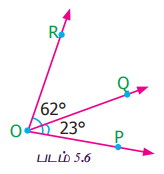
∠POR = ∠POQ + ∠QOR என நமக்குத் தெரியும்

62° = 23° + ∠QOR 

இருபுறமும் 23° ஐ கழிக்க 

62° - 23° = 23° + ∠QOR - 23°

∠QOR = 39°

எடுத்துக்காட்டு 5.3 

பின்வரும் அடுத்துள்ள கோண இணைகளில் எவை நேரிய கோண இணைகளாக அமையும்?

(i) 89°, 91°

(ii) 105°, 65°

(iii) 117°, 62° (iv) 40°, 140° 

தீர்வு 

(i)   89° + 91° = 180° என்பதால், இவை நேரிய கோண இணை ஆகும்.

(ii) 105° + 65° = 170° ≠ 180° என்பதால், இவை நேரிய கோண இணையாக அமையவில்லை . 

(iii) 117° + 62° = 179° ≠ 180° என்பதால், இவை நேரிய கோண இணையாக அமையவில்லை . 

(iv) 40° + 140° = 180° என்பதால் இவை நேரிய கோண இணையாகும்.

எடுத்துக்காட்டு 5.4 

விடுபட்ட கோணத்தைக் காண்க.

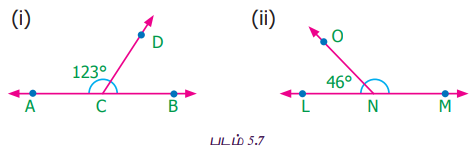
தீர்வு 

(i) கொடுக்கப்பட்ட கோணங்கள் நேரிய கோண இணை என்பதால்,

 ∠ACD +  ∠BCD = 180°

123° + ∠BCD = 180° 

இருபுறமும் 123° ஐக் கழிக்க 

123° + ∠BCD - 123° = 180° - 123°

∠BCD = 57° 

(ii) கொடுக்கப்பட்ட கோணங்கள் நேரிய கோண இணை என்பதால்,

∠LNO + ∠MNO = 180°

46° + ∠MNO = 180° 

இருபுறமும் 46° ஐக் கழிக்க

 46° + ∠MNO – 46° = 180° - 46°

∠MNO = 134° 

எடுத்துக்காட்டு 5.5 

இரண்டு கோணங்கள் 3:2 என்ற விகிதத்தில் உள்ளன. அவை நேரிய கோண இணைகள் எனில் அவற்றைக் காண்க.

தீர்வு 

தேவையான கோணங்கள் 3x மற்றும் 2 x என்க. 

அவை, நேரிய கோண இணை என்பதால், அவற்றின் கூடுதல் 180° ஆகும். 

எனவே,

3x +2x = 180°

5x = 180°

x = 180o / 5

x = 36o

அந்தக் கோணங்கள் 3 x = 3×36 = 108°

2 x = 2×36 = 72° 

நேரிய கோண இணைகள் - மேலும் சில முடிவுகள்

அமுதன் தனது ஆசிரியரிடம், நேரிய கோண இணைகளுக்கு இடையே ஒரு கதிரை வரைந்தால் என்னவாகும் என வினவினார். ஆசிரியர் அவரிடம் அதை வரைந்து காட்டுமாறு கூறினார். அமுதன், படம் 5.8-ல் உள்ளதைப் போன்று வரைந்து காட்டினார்.

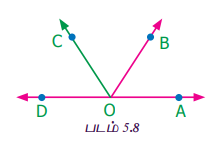
ஆசிரியர் அமுதனிடம், ∠AOB மற்றும் ∠BOC ஆகிய கோணங்களைக் குறித்து என்ன கூறுவாய் என வினவினார். அவை அடுத்துள்ள கோணங்களாகும் எனக் கூறினார். மேலும் ∠AOB + ∠BOC = ∠AOC என்பதும் உண்மையாகும். மேலும் ஆசிரியர்,  ∠AOC மற்றும் ∠COD ஆகிய கோணங்களைக் குறித்தும் வினவினார். அமுதன், அவை நேரிய கோண இணைகள் எனப் பதிலுரைத்தார். எனவே அவற்றின் கூடுதல் 180° ஆகும். அதாவது ∠AOC + ∠COD = 180°.

இரு முடிவுகளையும் இணைக்க நமக்குக் கிடைப்பது ∠AOB + ∠BOC + ∠COD = 180° .

எனவே, ஒரு நேர்கோட்டின் மீதுள்ள ஏதேனும் ஒரு புள்ளியில் அமையும் கோணம் 180° ஆகும்.

சிந்திக்க 

கீழே கொடுக்கப்பட்டுள்ள படத்தில் உள்ளவாறு, ஒரு நேர்க்கோட்டின் மீது 3 அல்லது 4 அல்லது 5 கதிர்கள் அமையும்போது என்ன நிகழும்?

நேரிய கோண இணைகளின் பற்றிய மேலும் ஒரு முடிவை நாம் கற்போம். படம்5.9 ஐ உற்று நோக்குக. AB என்பது ஒரு நேர்கோடு. OC ஆனது AB-ன் மீது O-ல் அமையும் ஒரு கதிர். 

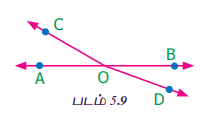
எனவே ∠AOC மற்றும் ∠BOC ஆகியவை நேரிய கோண இணை. 

ஆகவே, ∠AOC +  ∠BOC = 180° 

மேலும் OD ஆனது AB-ன் மீது O -ல் அமையும் மற்றொரு கதிர். மேலும் ∠AOD மற்றும் ∠BOD ஆனது நேரிய கோண இணை. ஆகவே, ∠AOD + ∠BOD = 180° 

இப்போது ∠AOC, ∠BOC, ∠AOD மற்றும் ∠BOD ஆகியவை O என்ற புள்ளியில் அமையும் கோணங்கள். 

(∠AOC + ∠BOC) + (∠AOD + ∠BOD) = 180° + 180° = 360° என்பதை நாம் காணலாம். 

ஆகவே, ஒரு புள்ளியில் அமையும் கோணங்களின் கூடுதல் 360° ஆகும்.

சிந்திக்க

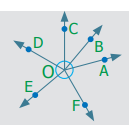
∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOF + ∠FOA = 360° என்ற கூற்றை நிரூபிக்க இயலுமா?

எடுத்துக்காட்டு 5.6

படம் 5.10 இல் ∠ROS இன் மதிப்பைக் காண்க. 

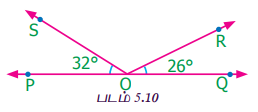
தீர்வு 

∠QOR + ∠ROS + ∠SOP = 180° என்பது நாம் அறிந்ததே 

26° + ∠ROS + 32° = 180°

∠ROS + 58° = 180° 

இரு புறமும் 58° ஐ கழிக்க

∠ROS = 180° - 58° = 122°

எடுத்துக்காட்டு 5.7

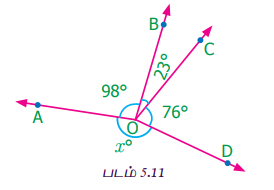
படம் 5.11 இல் இருந்து x o இன் மதிப்பைக் காண்க 

தீர்வு 

98° + 23° + 76° + x° = 360°

197° +x° = 360° 

x ° = 360° - 197° = 163°

3. குத்தெதிர்க் கோணங்கள்

நாம், வெட்டும் கோடுகளைக் குறித்து அறிந்துள்ளோம் படம் 5.12 இல், l மற்றும் m என்ற கோடுகள் O என்ற புள்ளியில் வெட்டிக்கொள்கின்றன. மேலும் வெட்டிக்கொள்ளும் புள்ளியில்  நான்கு கோணங்களை உருவாக்குகின்றன. அவையாவன: ∠1, ∠2, ∠3 மற்றும் ∠4.

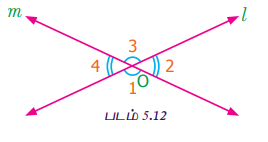
கோணம் ∠1 ஐக் கருதுக. கோணம் ∠1 க்கு ∠2 மற்றும் ∠4 ஆகியவை அடுத்தடுத்துள்ளக் கோணங்கள், ∠3 ஆனது அடுத்தமையாக் கோணம். இதே போன்று மற்ற மூன்று கோணங்களுக்கும் இரண்டு அடுத்தடுத்துள்ள கோணங்களும், ஒரு அடுத்தமையாக் கோணமும் உள்ளன. ஒரு கோணமும் அதன் அடுத்தமையாக் கோணமும், வெட்டிக் கொள்ளும் புள்ளி O (முனை)இல் ஒன்றுக்கொன்று எதிராக அமைந்துள்ளன.

இவ்வாறான கோணங்கள் முனையைப் பொறுத்து ஒன்றுக்கொன்று எதிராக அமையும். எனவே இவை குத்தெதிர்க் கோணங்கள் என்று அழைக்கப்படும்.

இரு கோடுகள் ஒன்றையொன்று வெட்டிக்கொள்ளும்போது உருவாகும் இரு சோடி அடுத்தமையாக் கோணங்கள், குத்தெதிர்க் கோணங்கள் என அழைக்கப்படும்.

இவற்றை முயல்க 

1. அன்றாட வாழ்வில் குத்தெதிர்க் கோணங்களுக்கான நான்கு எடுத்துக்காட்டுகள் கீழே கொடுக்கப்பட்டுள்ளன.

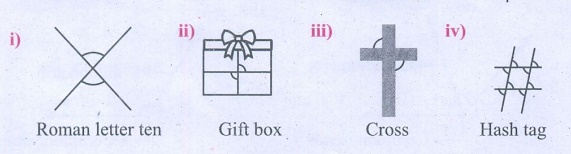
உங்களுடைய சுற்றுப்புறத்தில் காணப்படும், குத்தெதிர்க் கோணங்களுக்கான மேலும் நான்கு எடுத்துக்காட்டுகளைக் குறிப்பிடுக.

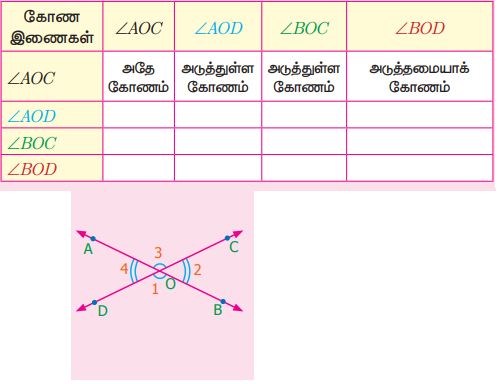
2. கொடுக்கப்பட்டுள்ள படத்தில்,   மற்றும்   என்ற இரு கோடுகள் O-வில் வெட்டிக்கொள்கின்றன. கோண இணைகளைக் கவனித்து அட்டவணையை நிறைவு செய்க. உங்களுக்காக ஒரு கட்டம் நிரப்பப்பட்டுள்ளது.

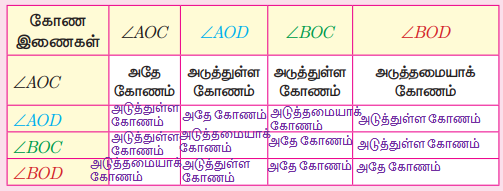
3. இரு சோடி குத்தெதிர்க் கோணங்களின் பெயர்களை எழுதுக.

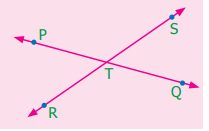
∠ PTS and ∠ RTQ

∠ PTR and ∠ STQ

 4. கீழே கொடுக்கப்பட்டுள்ள படத்தில் x° இன் மதிப்பைக் காண்க. 

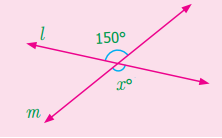
xo = 150o

செயல்பாடு

ஒரு காகிதத்தில்    மற்றும்   என்ற வெட்டும் கோடுகளை வரைக. அவைகள் O-என்ற புள்ளியில் வெட்டிக்கொள்ளட்டும். இரு சோடி குத்தெதிர்க் கோணங்களுக்கு ∠1, ∠2 என்றும் ∠3, ∠4 என்றும் பெயரிடுக. ∠2, ∠3 ஆகியவற்றைப் பிரதியெடுக்க. பிரதியெடுத்த கோணம் ∠2 ஐக் கோணம் ∠1 இன் மீது பொருத்துக. அவை சமமாக உள்ளனவா? அதேபோல், பிரதி எடுத்த கோணம் ∠3 ஐக் கோணம் ∠4 இன் மீது பொருத்துக. அவை சமமாக உள்ளனவா? இதற்கான முடிவுகளைப் பதிவு செய்து கலந்துரையாடுக.

மேற்கண்ட செயல்பாட்டின் மூலம் குத்தெதிர்க் கோணங்கள் சமமானவை என்று அறிகிறோம்.