Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ - Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї | 9th Maths : UNIT 3 : Algebra
9 Я«єЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ«БЯ«ЋЯ»ЇЯ«ЋЯ»Ђ : Я«ЁЯ«▓Я«ЋЯ»Ђ 3 : Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї
Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї
Я«ЁЯ«▓Я«ЋЯ»Ђ 3
Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ««Я»Ї
Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»ІЯ«▓Я»Ї Я«хЯ»ЄЯ«▒Я»єЯ«цЯ»ЂЯ«хЯ»ЂЯ««Я»Ї Я«еЯ«ЪЯ»ѕЯ««Я»ЂЯ«▒Я»ѕ Я«хЯ«ЙЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ»ѕЯ«»Я»ІЯ«ЪЯ»Ђ Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»ЂЯ«ЪЯ»ѕЯ«»Я«цЯ»Ђ Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕ Я«јЯ«Е Я«ЅЯ«▒Я»ЂЯ«цЯ«┐Я«»Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ѓЯ«▒ Я««Я»ЂЯ«ЪЯ«┐Я«»Я»ЂЯ««Я»Ї.
Рѕњ Я«фЯ«┐Я«░Я«ЙЯ«ЕЯ»Ї Я«▓Я»ЄЯ«фЯ»ІЯ«хЯ«┐Я«џЯ»Ї
Я«ЁЯ«▓Я»єЯ«ЋЯ»ЇЯ«ИЯ«ЙЯ«БЯ»ЇЯ«ЪЯ«┐Я«░Я«┐Я«»Я«ЙЯ«хЯ«┐Я«ЕЯ»Ї Я«ЪЯ»ѕЯ«»Я»ІЯ«фЯ«ЙЯ«ЕЯ»ЇЯ«ЪЯ«ИЯ»Ї (Diophantus) 84 Я«єЯ«БЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї Я«хЯ«ЙЯ«┤Я»ЇЯ«еЯ»ЇЯ«ц Я«ЋЯ«БЯ«┐Я«ц Я««Я»ЄЯ«цЯ»ѕЯ«»Я«ЙЯ«хЯ«ЙЯ«░Я»Ї. Я«ЄЯ«хЯ«░Я»Ї Я«ЋЯ«┐.Я«фЯ«┐.(Я«фЯ»і.Я«є) 201 Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЋЯ«┐.Я«фЯ«┐. (Я«фЯ»і.Я«є) 215 Я«ЄЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«фЯ«┐Я«▒Я«еЯ»ЇЯ«цЯ«хЯ«░Я»Ї. Я«ЄЯ«хЯ«░Я»Ї Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«хЯ«┐Я«»Я«▓Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒ Я«цЯ»іЯ«ЪЯ«░Я»Ї Я«фЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЋЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«єЯ«џЯ«┐Я«░Я«┐Я«»Я«░Я»Ї Я«єЯ«хЯ«ЙЯ«░Я»Ї. Я«ЄЯ«хЯ«░Я«цЯ»Ђ Я«фЯ»ЂЯ«цЯ»ЇЯ«цЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«џЯ»Ї Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»ђЯ«░Я»ЇЯ«хЯ»Ђ Я«фЯ«▒Я»ЇЯ«▒Я«┐ Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«цЯ«ЕЯ«хЯ«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«цЯ«еЯ»ЇЯ«цЯ»ѕ Я«јЯ«ЕЯ«хЯ»ЂЯ««Я»Ї Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«▒Я«ЙЯ«░Я»Ї.

Я«ЪЯ»ѕЯ«»Я»ІЯ«фЯ«ЙЯ«ЕЯ»ЇЯ«ЪЯ«ИЯ»Ї
Я«ЋЯ«▒Я»ЇЯ«▒Я«▓Я»Ї Я«хЯ«┐Я«│Я»ѕЯ«хЯ»ЂЯ«ЋЯ«│Я»Ї
Рђб Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ѕ Я«хЯ«ЋЯ»ѕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ«цЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«џЯ»Ї Я«џЯ»єЯ«»Я»ЇЯ«»Я»ЂЯ««Я»Ї Я«цЯ«┐Я«▒Я«ЕЯ«ЪЯ»ѕЯ«цЯ«▓Я»Ї.
Рђб Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ«▓Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»ѓЯ«џЯ»ЇЯ«џЯ«┐Я«»Я«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ«цЯ«▓Я»Ї.
Рђб Я««Я»ђЯ«цЯ«┐Я«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я««Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«цЯ»Ї Я«цЯ»ЄЯ«▒Я»ЇЯ«▒Я«цЯ»ЇЯ«цЯ»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ«цЯ«▓Я»Ї.
Рђб Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«ц Я««Я»ЂЯ«▒Я»ЇЯ«▒Я»іЯ«░Я»ЂЯ««Я»ѕЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«ЋЯ»Ї Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї.
Рђб Я«ЄЯ«░Я»ЂЯ«фЯ«ЪЯ«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я»ЂЯ«фЯ»ЇЯ«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї.
Рђб Я«цЯ»іЯ«ЋЯ»ЂЯ««Я»ЂЯ«▒Я»ѕ Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я«┐Я«▓Я»Ї Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«цЯ«▓Я»Ї.
Рђб Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ђЯ«фЯ»ЇЯ«фЯ»єЯ«░Я»Ђ Я«фЯ»іЯ«цЯ»Ђ Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«ЋЯ«ЙЯ«БЯ»ЂЯ«цЯ«▓Я»Ї.
Рђб Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«│Я»ЇЯ«│ Я«еЯ»ЄЯ«░Я«┐Я«» Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«цЯ«▓Я»Ї.
Рђб Я«ЄЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«ц Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ««Я»ѕЯ«еЯ»ЇЯ«ц Я«еЯ»ЄЯ«░Я«┐Я«» Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕ Я«хЯ«░Я»ѕЯ«фЯ«Ъ Я««Я»ЂЯ«▒Я»ѕ, Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«ц Я««Я»ЂЯ«▒Я»ѕЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я«цЯ»ђЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«▓Я»Ї.
Рђб Я«ЄЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«ЁЯ««Я»ѕЯ«еЯ»ЇЯ«ц Я«еЯ»ЄЯ«░Я«┐Я«» Я«џЯ««Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ««Я»ѕЯ«хЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«њЯ«░Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ««Я»ѕЯ«хЯ«▒Я»ЇЯ«▒ Я«цЯ«ЕЯ»ЇЯ««Я»ѕЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ«цЯ«▓Я»Ї.
Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ««Я»Ї
Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ѕ Я«ЈЯ«ЕЯ»Ї Я«ЋЯ«▒Я»ЇЯ«Ћ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї?
Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«» Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«еЯ»ЇЯ«ц Я«ЄЯ«»Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«ЪЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»Ђ. Я«ЄЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«хЯ»ѕ Я«еЯ»ђЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«ЕЯ»ЇЯ«ЕЯ«░Я»Є Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«цЯ»ЇЯ«ц, Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я««Я»ЂЯ«┤Я»ЂЯ««Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»ЇЯ«фЯ«ЪЯ«ЙЯ«ц Я«еЯ«БЯ»ЇЯ«фЯ«░Я»ЇЯ«ЋЯ«│Я»Є! Я«ЄЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ«┐Я«▒Я«ЋЯ»Ђ Я«хЯ«░Я»ЂЯ««Я»Ї Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ«фЯ»Ї Я«фЯ«»Я«БЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»ЂЯ««Я»Ї, Я«ЄЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»Ї Я«ЅЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«еЯ«БЯ»ЇЯ«фЯ«░Я»ЇЯ«ЋЯ«│Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«»Я«БЯ«┐Я«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ«ЋЯ»ЇЯ«Ћ Я«хЯ«ЋЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЄЯ«хЯ«░Я»ЇЯ«ЋЯ«│Я»ѕ Я«еЯ«ЙЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї, Я«ЅЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я««Я»ЂЯ«┤Я»ЂЯ««Я»ѕЯ«»Я«ЙЯ«Ћ Я«ЁЯ«▒Я«┐Я««Я»ЂЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«ц Я«ЅЯ«│Я»ЇЯ«│Я»ІЯ««Я»Ї.
(a+1)2 = a2 + 2a + 1
Я«ЄЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕ. Я«фЯ«ЙЯ«░Я»ЇЯ«фЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЂЯ«џЯ»Ї Я«џЯ«┐Я«▒Я«фЯ»ЇЯ«фЯ»Ђ Я«хЯ«ЙЯ«»Я»ЇЯ«еЯ»ЇЯ«цЯ«цЯ«ЙЯ«ЋЯ«цЯ»Ї Я«цЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ. Я«ЄЯ«▓Я»ЇЯ«▓Я»ѕЯ«»Я«Й? Я«еЯ«ЙЯ««Я»Ї Я««Я»ЂЯ«ЕЯ»ЇЯ«фЯ»Є Я«еЯ«┐Я«▒Я»ѕЯ«» Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«ЙЯ«░Я»ЇЯ«цЯ»ЇЯ«цЯ«┐Я«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. Я«јЯ«ЕЯ«хЯ»Є, Я«ЈЯ«ЕЯ»Ї Я«ЄЯ«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«фЯ»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«ЋЯ»Ї Я«ЋЯ«хЯ«▓Я»ѕЯ«фЯ»ЇЯ«фЯ«Ъ Я«хЯ»ЄЯ«БЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї? Я«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї, Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»Ї Я«ЈЯ«ЕЯ»Ї Я««Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«»Я«цЯ»ЇЯ«цЯ»ЂЯ«хЯ««Я»Ї Я«хЯ«ЙЯ«»Я»ЇЯ«еЯ»ЇЯ«цЯ«хЯ»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»ЂЯ«фЯ»Ї Я«фЯ«▓ Я«ЋЯ«ЙЯ«░Я«БЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«ЅЯ«│Я»ЇЯ«│Я«Е.
Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕ Я«ЁЯ«▒Я«┐Я«» Я«ЊЯ«░Я»Ї Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ»ІЯ««Я»Ї. Я«еЯ«ЙЯ««Я»Ї Я«јЯ«БЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«еЯ«┐Я«▒Я»ѕЯ«»Я«ЋЯ»Ї Я«ЋЯ«▒Я»ЇЯ«▒Я»Ђ, Я«ЁЯ«цЯ«ЕЯ»ЇЯ«фЯ«┐Я«ЕЯ»Ї Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«цЯ»єЯ«░Я«┐Я«»Я«ЙЯ«ц Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«фЯ«▒Я»ЇЯ«▒Я«┐Я«џЯ»Ї Я«џЯ«┐Я«еЯ»ЇЯ«цЯ«┐Я«цЯ»ЇЯ«цЯ»ІЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ«┐Я«▓Я»Ї Я«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї.
Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї, Я«еЯ«ЙЯ««Я»Ї Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я«┐Я«ЪЯ««Я»Ї Я«цЯ«┐Я«░Я»ЂЯ««Я»ЇЯ«фЯ«џЯ»Ї Я«џЯ»єЯ«ЕЯ»ЇЯ«▒Я»Ђ, Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«ц Я««Я»іЯ«┤Я«┐Я«»Я«┐Я«▓Я»Ї Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«јЯ«┤Я»ЂЯ«ц Я««Я»ЂЯ«»Я«▓Я»ЇЯ«хЯ»ІЯ««Я»Ї.
5418 Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЊЯ«░Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«хЯ«ЕЯ«┐Я«»Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї. Я«ЄЯ«цЯ»Ђ Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї Рђю5РђЮ Я«єЯ«»Я«┐Я«░Я««Я»Ї Рђю4РђЮ Я«еЯ»ѓЯ«▒Я»Ђ Рђю1РђЮ Я«фЯ«цЯ»ЇЯ«цЯ»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Рђю8РђЮ Я«њЯ«ЕЯ»ЇЯ«▒Я»ЂЯ«ЋЯ«│Я»Ї.
Я«ЄЯ«цЯ»ѕЯ«ЋЯ»Ї Я«фЯ«┐Я«ЕЯ»ЇЯ«хЯ«░Я»ЂЯ««Я«ЙЯ«▒Я»Ђ Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї
5 ├Ќ 1000 + 4 ├Ќ 100 + 1 ├Ќ 10 + 8
Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї, Я«ЄЯ«цЯ«ЕЯ»ѕ
5 ├Ќ 103 + 4 ├Ќ 102 + 1 ├Ќ 101 + 8 Я«јЯ«ЕЯ»ЇЯ«▒Я«хЯ«ЙЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ«▓Я«ЙЯ««Я»Ї:
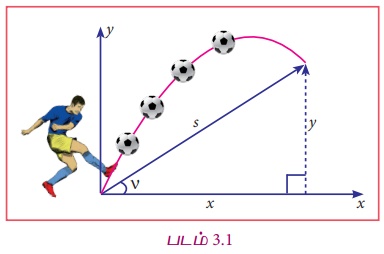
Я«ЄЯ«цЯ»Ђ 5x3 + 4x2 + x + 8 Я«јЯ«ЕЯ»ЇЯ«▒ Я«хЯ«ЪЯ«┐Я«хЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«цЯ»єЯ«│Я«┐Я«хЯ»Ђ. Я«ЄЯ«еЯ»ЇЯ«ц Я«хЯ«ЪЯ«┐Я«хЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«хЯ«цЯ»Ђ Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«фЯ«»Я«ЕЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї? Я«еЯ«ЙЯ««Я»Ї Я«јЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«цЯ»Ї Я«цЯ«џЯ««Я«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»ЇЯ«цЯ«ЙЯ«ЕЯ»Є. Я«єЯ«ЋЯ»ѕЯ«»Я«ЙЯ«▓Я»Ї Я«јЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»ЂЯ««Я»Ї x = 10. Я«фЯ«┐Я«ЕЯ»Ї Я«ЄЯ«цЯ«┐Я«▓Я»Ї Я«јЯ«ЕЯ»ЇЯ«Е Я«хЯ»ЄЯ«ЪЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ѕ? Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«хЯ«┐Я«цЯ«┐Я«ЋЯ«│Я»Ї Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ»ЂЯ«│Я»ЇЯ«│Я«цЯ«Й? Я«ЊЯ«░Я»Ї Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«ЕЯ»Ї Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»Ї 3 Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«▓Я»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Є, Я«ЁЯ«еЯ»ЇЯ«ц Я«јЯ«БЯ»Ї 3 Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«еЯ«┐Я«ЕЯ»ѕЯ«хЯ»Ђ Я«ЋЯ»іЯ«│Я»ЇЯ«│Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї. x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ 3 Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«ц Я«фЯ«┐Я«▒Я«ЋЯ»Ђ Я««Я»ђЯ«цЯ«┐ 1 Я«хЯ«░Я»ЂЯ«ЋЯ«┐Я«▒Я«цЯ»єЯ«ЕЯ«┐Я«▓Я»Ї, x2, x3, Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЄЯ«цЯ»Ђ Я«фЯ»іЯ«░Я»ЂЯ«еЯ»ЇЯ«цЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«хЯ«ЕЯ«┐Я«»Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї. Я«ЄЯ«хЯ»ѕ Я«јЯ«▓Я»ЇЯ«▓Я«ЙЯ««Я»Ї 3 Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«фЯ«┐Я«▒Я«ЋЯ»Ђ, 1 Я«љ Я««Я»ђЯ«цЯ«┐Я«»Я«ЙЯ«ЋЯ«цЯ»Ї Я«цЯ«░Я»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«јЯ«ЕЯ«хЯ»Є Я«њЯ«хЯ»ЇЯ«хЯ»ІЯ«░Я»Ї Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї 1 Я«єЯ«▓Я»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐ Я«ЁЯ«хЯ»ѕ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«ЕЯ«ЙЯ«▓Я»Ї, Я««Я»іЯ«цЯ»ЇЯ«ц Я«ЄЯ«▓Я«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЋЯ»ѓЯ«ЪЯ»ЂЯ«цЯ«▓Я»ѕ Я«еЯ»ђЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«фЯ»єЯ«▒Я»ЂЯ«ЋЯ«┐Я«▒Я»ђЯ«░Я»ЇЯ«ЋЯ«│Я»Ї. Я«ЁЯ«цЯ»Ђ 3 Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«јЯ«ЕЯ«┐Я«▓Я»Ї, Я««Я»іЯ«цЯ»ЇЯ«ц Я«јЯ«БЯ»ЇЯ«БЯ«┐Я«▒Я»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«ЁЯ«цЯ»ЄЯ«цЯ«ЙЯ«ЕЯ»Ї. 9 Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«┐Я«цЯ«┐, 2 Я«ЁЯ«▓Я»ЇЯ«▓Я«цЯ»Ђ 5 Я«єЯ«▓Я»Ї Я«хЯ«ЋЯ»ЂЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«хЯ«┐Я«цЯ«┐ Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЄЯ«цЯ»ЄЯ«фЯ»ІЯ«▓ Я«јЯ«│Я«┐Я«цЯ«ЙЯ«Ћ Я««Я»єЯ«»Я»ЇЯ«фЯ«┐Я«ЋЯ»ЇЯ«Ћ Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї.
Я«еЯ««Я«цЯ»Ђ Я«еЯ»ІЯ«ЋЯ»ЇЯ«ЋЯ««Я»Ї Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«хЯ«┐Я«цЯ«┐Я«ЋЯ«│Я»ѕ Я«еЯ«┐Я«░Я»ѓЯ«фЯ«┐Я«фЯ»ЇЯ«фЯ«цЯ»Ђ Я«ЁЯ«▓Я»ЇЯ«▓. Я«єЯ«ЕЯ«ЙЯ«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«хЯ»ѕ Я«фЯ«▓ Я«фЯ»ЂЯ«цЯ«┐Я«» Я«јЯ«БЯ»Ї Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕ Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я«хЯ»єЯ«│Я«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«хЯ«цЯ»Є Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я«џЯ»іЯ«▓Я»ЇЯ«▓Я«фЯ»Ї Я«фЯ»ІЯ«ЕЯ«ЙЯ«▓Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»Ї Я«фЯ«▓Я«хЯ«ЋЯ»ѕ Я«фЯ»іЯ«░Я»ЂЯ«ЪЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я«ЙЯ«ЋЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«ЁЯ«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я«┐Я«░Я»ЂЯ«еЯ»ЇЯ«цЯ»Ђ Я«еЯ«ЙЯ««Я»Ї Я«фЯ«▓Я«хЯ«▒Я»ЇЯ«▒Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│ Я«ЄЯ«»Я«▓Я»ЂЯ««Я»Ї.
Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»Ї x2, 5x2 Рѕњ 3, 2x+7 Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«▒Я»ЇЯ«▒Я»ѕ x Я«ЄЯ«ЕЯ»Ї Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«ЙЯ«Ћ Я«еЯ«ЙЯ««Я»Ї Я«ЅЯ«БЯ«░Я«▓Я«ЙЯ««Я»Ї. x Я««Я«ЙЯ«▒Я»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я««Я«ЙЯ«▒Я»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«ЙЯ«БЯ»ЇЯ«фЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я«еЯ«ЙЯ««Я»Ї Я«њЯ«░Я»Ђ Я«хЯ«░Я»ѕЯ«фЯ«ЪЯ««Я»Ї Я«хЯ«░Я»ѕЯ«еЯ»ЇЯ«цЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«цЯ»Ђ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ѕЯ«фЯ»Ї Я«фЯ»ЂЯ«░Я«┐Я«еЯ»ЇЯ«цЯ»Ђ Я«ЋЯ»іЯ«│Я»ЇЯ«│ Я««Я«┐Я«ЋЯ«хЯ»ЂЯ««Я»Ї Я«ЅЯ«цЯ«хЯ«┐Я«»Я«ЙЯ«Ћ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«фЯ»ЇЯ«фЯ»ІЯ«цЯ»Ђ Я«ЁЯ«▒Я«┐Я«хЯ«┐Я«»Я«▓Я»Ї, Я«фЯ»іЯ«▒Я«┐Я«»Я«┐Я«»Я«▓Я»Ї, Я«хЯ«БЯ«┐Я«Ћ Я«єЯ«»Я»ЇЯ«хЯ»ЂЯ«ЋЯ«│Я»Ї, Я«фЯ»іЯ«░Я»ЂЯ«│Я«ЙЯ«цЯ«ЙЯ«░Я««Я»Ї Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я«▓Я»ЇЯ«▓Я«ЙЯ««Я«▓Я»Ї Я«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«▓Я»ЂЯ««Я»Ї Я«ЋЯ»ѓЯ«Ъ Я«еЯ«ЙЯ««Я»Ї Я«џЯ«еЯ»ЇЯ«цЯ«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«еЯ«▓Я»ЇЯ«▓ Я«фЯ«▓ Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я»ЂЯ«┤Я»ЂЯ«хЯ«цЯ»ЂЯ««Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я»ѕЯ«фЯ»Ї Я«фЯ«┐Я«░Я«цЯ«┐Я«фЯ«▓Я«┐Я«ЋЯ»ЇЯ«ЋЯ«ЙЯ«хЯ«┐Я«ЪЯ«┐Я«ЕЯ»ЂЯ««Я»Ї, Я«ЁЯ«хЯ»ѕ Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»Ї Я«ЁЯ««Я»ѕЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЅЯ«БЯ»ЇЯ««Я»ѕЯ«»Я«┐Я«▓Я»Ї, Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«цЯ»ІЯ«░Я«ЙЯ«»Я««Я«ЙЯ«Е Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЅЯ«»Я«░Я»Ї Я«ЋЯ«БЯ«┐Я«цЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«░Я»ЂЯ«фЯ»ЇЯ«фЯ»іЯ«░Я»ЂЯ«│Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«ЄЯ«цЯ»Є Я«ЋЯ«░Я»ЂЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«фЯ«▓Я«░Я»Ї Я«цЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«хЯ«ЙЯ«┤Я»ЇЯ«хЯ«┐Я«»Я«▓Я»Ї Я««Я»ЂЯ«▒Я»ѕЯ«»Я»ѕ Я«јЯ«│Я«┐Я«цЯ«ЙЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«ЕЯ«░Я»Ї.

Я«ЅЯ«»Я«┐Я«░Я«┐Я«»Я«▓Я»Ї, Я«ЋЯ«БЯ«┐Я«ЕЯ«┐ Я«ЁЯ«▒Я«┐Я«хЯ«┐Я«»Я«▓Я»Ї, Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«фЯ»Ђ Я«ЁЯ««Я»ѕЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«▒Я»ЇЯ«▒Я«┐Я«▓Я»Ї Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»Ї Я««Я«┐Я«ЋЯ«фЯ»Ї Я«фЯ«░Я«хЯ«▓Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«ЄЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ«┐Я«»Я«▓Я»Ї Я«цЯ»іЯ«ЪЯ«░Я»ЇЯ«еЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»іЯ«БЯ»ЇЯ«ЪЯ»Є Я«џЯ»єЯ«▓Я»ЇЯ«ЋЯ«┐Я«▒Я«цЯ»Ђ. Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«фЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї (Я«фЯ«ЪЯ««Я»Ї 3.1, 3.2, Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї 3.3) Я«ЊЯ«░Я»Ї Я«ЄЯ«░Я»ЂЯ«фЯ«ЪЯ«┐ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї. Я«еЯ«ЙЯ««Я»Ї, Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«Е Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»ѕ Я««Я«ЪЯ»ЇЯ«ЪЯ»ЂЯ««Я»Ї Я«ЋЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│Я«фЯ»Ї Я«фЯ»ІЯ«хЯ«цЯ«┐Я«▓Я»ЇЯ«▓Я»ѕ. Я«ЁЯ«цЯ«▒Я»ЇЯ«ЋЯ»Ђ Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«јЯ«хЯ»ЇЯ«хЯ«ЙЯ«▒Я»Ђ Я«ЋЯ»ѓЯ«ЪЯ»ЇЯ«ЪЯ«▓Я»Ї, Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї, Я«хЯ«ЋЯ»ЂЯ«цЯ»ЇЯ«цЯ«▓Я»Ї Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒Я«хЯ«▒Я»ЇЯ«▒Я»ѕ Я«ЋЯ«▒Я»ЇЯ«▒Я»ЂЯ«│Я»ЇЯ«│Я»ІЯ««Я»І Я«ЁЯ«цЯ»Є Я«фЯ»ІЯ«▓Я»Ї Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я«┐Я«▓Я»ЂЯ««Я»Ї Я«ЋЯ«▒Я»ЇЯ«▒Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»іЯ«│Я»ЇЯ«│ Я«ЄЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
Я«ЋЯ»іЯ«ЪЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«фЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ«хЯ«ЕЯ«┐Я«»Я»ЂЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї
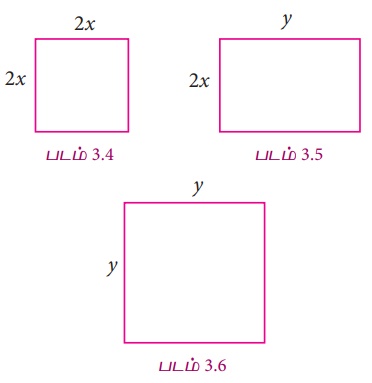
Я««Я»ЄЯ«▓Я»Є Я«ЅЯ«│Я»ЇЯ«│ 3 Я«фЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я»іЯ«цЯ»ЇЯ«цЯ«фЯ»Ї Я«фЯ«░Я«фЯ»ЇЯ«фЯ«│Я«хЯ»Ђ 4x2 + 2xy + y2, Я«ЄЯ«еЯ»ЇЯ«цЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я»ѕ Я«еЯ«ЙЯ««Я»Ї Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕ Я«јЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Є x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y Рѕњ Я«ЋЯ»ЇЯ«ЋЯ»Ђ Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я«ЙЯ«Е Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЁЯ«│Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«фЯ»ІЯ«цЯ»Ђ Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«фЯ«░Я«фЯ»ЇЯ«фЯ«│Я«хЯ»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. x Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї y Я«фЯ«ЋЯ»ЇЯ«ЋЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я«ЙЯ«▒Я«ЋЯ»ЇЯ«ЋЯ»ѓЯ«ЪЯ«┐Я«»Я«цЯ«ЙЯ«Ћ Я«ЅЯ«│Я»ЇЯ«│Я«цЯ«ЙЯ«▓Я»Ї, Я«ЁЯ«хЯ»ѕ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«јЯ«ЕЯ«хЯ»Є Я««Я«ЙЯ«▒Я«┐ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«хЯ»єЯ«хЯ»ЇЯ«хЯ»ЄЯ«▒Я»Ђ Я«јЯ«БЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«хЯ«┤Я«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«Ћ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї x, y, z Я«фЯ»ІЯ«ЕЯ»ЇЯ«▒ Я«јЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«фЯ»ЇЯ«фЯ«┐Я«ЪЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я««Я»ЄЯ«▒Я»ЇЯ«ЋЯ«БЯ»ЇЯ«Ъ Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«ЅЯ«│Я»ЇЯ«│ 4, 2 Я«јЯ«ЕЯ»ЇЯ«фЯ«хЯ»ѕ Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»Ї Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«Е. Я«јЯ«ЕЯ«хЯ»Є Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«еЯ«┐Я«▓Я»ѕЯ«»Я«ЙЯ«Е Я«јЯ«БЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»Ђ Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»Ђ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»Ї (Constants)
Я«јЯ«еЯ»ЇЯ«ц Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«БЯ»ЂЯ««Я»Ї Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«»Я»Є. Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЙЯ«ЪЯ»ЂЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ«┐ Я«јЯ«БЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ѕ Я«ЁЯ««Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«▓Я«ЙЯ««Я»Ї.
Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї 1, 5, Рѕњ32, 3/7, РѕњРѕџ2, 8.432, 1000000 Я«ЄЯ«ЕЯ»ЇЯ«ЕЯ»ЂЯ««Я»Ї Я«фЯ«┐Я«▒.
Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї (Variables)
Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я«┐Я«▓Я»Ї Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я»ѕ Я«ЄЯ«БЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«њЯ«░Я»Ђ Я«хЯ«░Я««Я»ЇЯ«фЯ«┐Я«▒Я»ЇЯ«ЋЯ»Ђ Я«ЅЯ«ЪЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«Ъ Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«хЯ«┤Я«┐Я«ЋЯ«│Я«┐Я«▓Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї Я«њЯ«░Я»Ђ Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. Я«еЯ«ЙЯ««Я»Ї Я«ЁЯ«▒Я«┐Я«еЯ»ЇЯ«ц 2¤ђr Я«єЯ«ЕЯ«цЯ»Ђ Я«єЯ«░Я««Я»Ї r Я«ЅЯ«ЪЯ»ѕЯ«» Я«хЯ«ЪЯ»ЇЯ«ЪЯ«цЯ»ЇЯ«цЯ«┐Я«ЕЯ»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я«│Я«хЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«ЋЯ«┐Я«ЕЯ»ЇЯ«▒Я«цЯ»Ђ. Я«еЯ«ЙЯ««Я»Ї r Я«ЄЯ«ЕЯ»Ї Я««Я«цЯ«┐Я«фЯ»ЇЯ«фЯ»ѕ 1 Я«џЯ»єЯ««Я»ђ, 4 Я«џЯ»єЯ««Я»ђ, 9 Я«џЯ»єЯ««Я»ђ ... Я«јЯ«Е Я««Я«ЙЯ«▒Я»ЇЯ«▒Я«┐Я«ЕЯ«ЙЯ«▓Я»Ї 2¤ђ, 8¤ђ, 18¤ђ .... Я«јЯ«ЕЯ»ЇЯ«▒ Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я«│Я«хЯ»ЂЯ«ЋЯ«│Я»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«фЯ»єЯ«░Я«┐Я«» Я«хЯ«ЪЯ»ЇЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я»Ї Я«еЯ««Я«ЋЯ»ЇЯ«ЋЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ«┐Я«ЪЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«еЯ»ЇЯ«ц 2¤ђr Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я«ЙЯ«ЕЯ«цЯ»Ђ Я«ЁЯ«ЕЯ»ѕЯ«цЯ»ЇЯ«цЯ»Ђ Я«хЯ«ЪЯ»ЇЯ«ЪЯ«ЎЯ»ЇЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«џЯ»ЂЯ«▒Я»ЇЯ«▒Я«│Я«хЯ»ЂЯ«ЋЯ«│Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ»ЂЯ««Я«ЙЯ«Е Я«џЯ«┐Я«▒Я«┐Я«» Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«цЯ»ЂЯ«▓Я»ЇЯ«▓Я«┐Я«»Я««Я«ЙЯ«Е Я«хЯ«┐Я«│Я«ЋЯ»ЇЯ«ЋЯ««Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«еЯ«ЙЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«џЯ»Ї Я«џЯ»єЯ«»Я«▓Я»ЇЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ѕ Я«ЄЯ«БЯ»ѕЯ«цЯ»ЇЯ«цЯ»ЂЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ««Я»ЇЯ«фЯ»ІЯ«цЯ»Ђ, Я«џЯ«ЙЯ«░Я»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»Ї Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«јЯ«БЯ»ЇЯ«ЋЯ«│Я»Ї Я«јЯ«ЕЯ»ЇЯ«▒ Я«ЅЯ«»Я«░Я»ЇЯ«цЯ«░ Я««Я»іЯ«┤Я«┐Я«»Я»ѕЯ«фЯ»Ї Я«фЯ»єЯ«▒Я»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї. Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я»Ї Я«јЯ«Е Я«ЁЯ«┤Я»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї Я«цЯ»єЯ«░Я«┐Я«»Я«ЙЯ«ц Я««Я»єЯ«»Я»ЇЯ«»Я»єЯ«БЯ»ЇЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«ЋЯ»ЇЯ«Ћ x,y,a,b Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я«фЯ«▓ Я«јЯ«┤Я»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»ѕЯ«фЯ»Ї Я«фЯ«»Я«ЕЯ»ЇЯ«фЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ«┐Я«▒Я»ІЯ««Я»Ї.
Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕ (Algebraic Expression)
Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕ Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«еЯ«ЙЯ«ЕЯ»ЇЯ«ЋЯ»Ђ Я«ЁЯ«ЪЯ«┐Я«фЯ»ЇЯ«фЯ«ЪЯ»ѕЯ«ЋЯ»Ї Я«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ЂЯ«▒Я«┐Я«»Я»ђЯ«ЪЯ»ЂЯ«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«ЅЯ«цЯ«хЯ«┐Я«»Я»ЂЯ«ЪЯ«ЕЯ»Ї Я««Я«ЙЯ«▒Я«┐ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я«ЙЯ«▓Я»Ї Я«ЄЯ«БЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЇЯ«ЪЯ»Ђ Я«ЁЯ««Я»ѕЯ«»Я»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«хЯ»ѕ Я«єЯ«ЋЯ»ЂЯ««Я»Ї.
Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ»ЇЯ«ЋЯ»Ђ Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ»ЂЯ«ЋЯ«│Я»Ї
x3 РђЊ 4x2 + 8x РђЊ 1, 4xy2 + 3x2y РђЊ 5/4 xy + 9, 5x2 РђЊ 7x + 6
Я«ЋЯ»єЯ«┤Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«│Я»Ї (Coefficients)
Я«њЯ«░Я»Ђ Я«фЯ«▓Я»ЇЯ«▓Я»ЂЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я«┐Я«▓Я»Ї Я«њЯ«хЯ»ЇЯ«хЯ»іЯ«░Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ«┐Я«▓Я»ЂЯ««Я»Ї Я«ЅЯ«│Я»ЇЯ«│ Я««Я«ЙЯ«▒Я«┐Я«ЋЯ«│Я«┐Я«ЕЯ»Ї Я«фЯ»єЯ«░Я»ЂЯ«ЋЯ»ЇЯ«ЋЯ«▓Я»Ї Я«ЋЯ«ЙЯ«░Я«БЯ«┐Я«»Я»Є Я«ЁЯ«цЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ Я«јЯ«ЕЯ«фЯ»ЇЯ«фЯ«ЪЯ»ЂЯ««Я»Ї.
Я«јЯ«ЪЯ»ЂЯ«цЯ»ЇЯ«цЯ»ЂЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«ЪЯ»ЇЯ«ЪЯ«ЙЯ«Ћ,
x2 + 5x Рѕњ 24 Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я««Я»ѓЯ«ЕЯ»ЇЯ«▒Я»Ђ Я«ЅЯ«▒Я»ЂЯ«фЯ»ЇЯ«фЯ»ЂЯ«ЋЯ«│Я»ѕЯ«ЋЯ»Ї Я«ЋЯ»іЯ«БЯ»ЇЯ«Ъ Я«ЄЯ«»Я«▒Я»ЇЯ«ЋЯ«БЯ«┐Я«цЯ«ЋЯ»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«»Я«ЙЯ«ЋЯ»ЂЯ««Я»Ї. Я«ЄЯ«ЎЯ»ЇЯ«ЋЯ»Ђ x Я«јЯ«ЕЯ»ЇЯ«фЯ«цЯ»Ђ Я«њЯ«░Я»Ђ Я««Я«ЙЯ«▒Я«┐. x2 Я«ЄЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ 1 Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї x Я«ЄЯ«ЕЯ»Ї Я«ЋЯ»єЯ«┤Я»Ђ 5 Я«єЯ«ЋЯ»ЂЯ««Я»Ї. Я««Я»ЄЯ«▓Я»ЂЯ««Я»Ї Рѕњ24 Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐ Я«єЯ«ЋЯ»ЂЯ««Я»Ї (24 Я«ЁЯ«▓Я»ЇЯ«▓).
Я«џЯ»єЯ«»Я«▓Я»ЇЯ«фЯ«ЙЯ«ЪЯ»Ђ 1
Я«ЋЯ»ђЯ«┤Я»ЇЯ«ЋЯ»ЇЯ«ЋЯ«ЙЯ«БЯ»ЂЯ««Я»Ї Я«ЋЯ»ІЯ«хЯ»ѕЯ«ЋЯ«│Я»ѕ Я««Я«ЙЯ«▒Я«┐, Я«ЋЯ»єЯ«┤Я»Ђ Я««Я«▒Я»ЇЯ«▒Я»ЂЯ««Я»Ї Я««Я«ЙЯ«▒Я«┐Я«▓Я«┐Я«ЋЯ«│Я«ЙЯ«ЋЯ«фЯ»Ї Я«фЯ«┐Я«░Я«┐Я«цЯ»ЇЯ«цЯ»Ђ Я«јЯ«┤Я»ЂЯ«цЯ»ЂЯ«Ћ.
