தீர்க்கப்பட்ட எடுத்துக்காட்டு கணக்குகள்: மேற்பொருந்துதல் தத்துவம்

அலைகளின் குறுக்கீட்டு விளைவு

எடுத்துக்காட்டு 11.16

படத்தில் காட்டியபடி A, B என்ற இரு மூலங்களைக் கருதுக. இரு மூலங்களும் ஒத்த அதிர்வெண்ணும், வேறுபட்ட வீச்சுகளும் அடைய இரு சீரிசை அலைகளை ஒத்த கட்டத்தில் வெளிவிடுகின்றன. O என்பது ஏதேனும் ஒரு புள்ளி இது கீழ்க்கண்ட படத்தில் காட்டியவாறு மூலங்கள் A,B யை இணைக்கும் கோட்டை இரு சமக்கூறாக்குகிறது. O,Y,X புள்ளிகளில் செறிவுகளைக் காண்க.

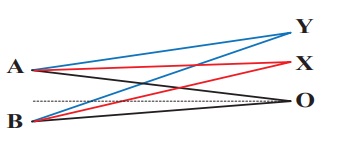
தீர்வு :

OA, OB சமநீளம் உடையது. எனவே A, B யிலிருந்து கிளம்பும் அலைகள் சம் தொலைவைக் (சம பாதை நீளங்கள்) கடந்து O வில் சந்திக்கின்றன. எனவே, O வில் இரு அலைகளுக்கிடையேயான பாதை வேறுபாடு சுழி.

OA - OB = 0

இரு அலைகளும் O வில் ஒத்தக் கட்டத்தில் சந்திப்பால், அவற்றிக்கிடையேயான கட்ட வேறுபாடு சுழியாகிறது. எனவே O வில் இரு அலைகளுக்கிடையேயான பாதை வேறுபாடு சுழியாவதால் செறிவு பெருமமாகும்

Y புள்ளியைக் கருதுக. பாதை வேறுபாடு λ வாக இருந்தால், Y ல் கட்ட வேறுபாடு

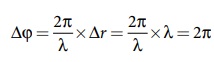
எனவே, Y ல் சந்திக்கும் இரு அலைகளும் ஒத்தக்கட்டத்தில் உள்ளதால், செறிவு பெருமமாக இருக்கும்.

X புள்ளியைக் கருதுக. பாதை வேறுபாடு λ/2 வாக இருந்தால் கட்ட வேறுபாடு

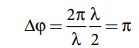
எனவே, X ல் சந்திக்கும் அலைகள் எதிர்க்கட்டத்தில் உள்ளதால், செறிவு சிறுமமாக இருக்கும்.

எடுத்துக்காட்டு 11.17

C, E என்ற இரு ஒலிப்பான்கள் (Speakers) 5 m இடைவெளியில் பிரித்து வைக்கப்பட்டு, ஒரே ஒலி மூலத்துடன் இணைக்கப்பட்டுள்ளன. C, E ன் மையம் O விலிருந்து 10m தொலைவிலுள்ள புள்ளி A ல் மனிதன் ஒருவன் நின்று கொண்டுள்ளான். A யிலிருந்து 1m தொலைவிலுள்ள B என்ற புள்ளிக்கு (OC க்கு இணையாக) நடந்து செல்கிறான் (படத்தில் காட்டியவாறு) B ல் ஒலிகளின் முதல் சிறுமத்தை உணர்கிறான். ஒலி மூலத்தின் அதிர்வெண்ணைக் காண்க. (ஒலியின் திசைவேகம் 343 ms-1 எனக் கொள்க).

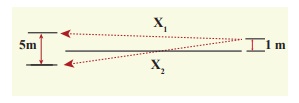
தீர்வு: 

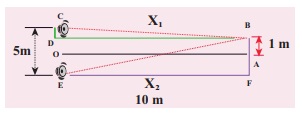
B யில் இரு ஒலி அலைகளும் 180° (எதிர்கட்டம்) ல் சந்தித்தால், முதல் சிறுமம் ஏற்படும்.

பாதை வேறுபாடு ∆x = λ/2.

பாதை வேறுபாட்டைக்காண பாதை நீளங்கள்  x1, x2 வைக் காண வேண்டும். 

செங்கோண முக்கோணம் BDC ல்,

செங்கோண முக்கோணம் EFB ல்,

பாதை வேறுபாடு ∆x = x2 − x1 = 10.6 m−10.1 m = 0.5 m இந்த பாதை வேறுபாடு λ/2 விற்கு சமமாக வேண்டும்.

ஒலி மூலத்தின் அதிர்வெண் காண,

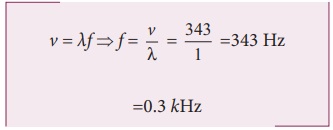
விம்மல்கள் தோன்றும் வீதம்

எடுத்துக்காட்டு 11.18:

5 m, 6 m அலைநீளம் கொண்ட இரண்டு ஒலி மூலங்களைக் கருதுக. இவை இரண்டும் வாயு ஒன்றில் 330 ms-1. திசைவேகத்துடன் செல்கின்றன. ஒரு வினாடியில் ஏற்படும் விம்மல்களின் எண்ணிக்கையை காண்க.

தீர்வு :

கொடுக்கப்பட்டது, λ1 = 5m,  λ2 = 6m v = 330 ms-1 திசை வேகத்திற்கும் அலைநீளத்திற்கு இடையேயானத் தொடர்பு

v = λf => f = v/λ

λ1 அலைநீள ஒலியின் அதிர்வெண்

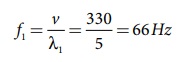
λ2 அலைநீள ஒலியின் அதிர்வெண்

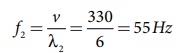
ஒரு வினாடியில் ஏற்படும் விம்மல்கள்

| f1 − f2| = |66 − 55| = 11 விம்மல்கள்/வினாடி (beats/sec)

எடுத்துக்காட்டு 11.19 

அதிர்வுறும் இரு இசைக்கவைகள் தோற்றுவிக்கும் அலைகளின் அலைச் சமன்பாடுகள் y1 = 5 sin(240π t) and y2 = 4 sin(244πt) தோன்றும் விம்மல்களின் எண்ணிக்கையை கணக்கிடுக. 

தீர்வு: 

கொடுக்கப்பட்டது y1 = 5 sin(240π t), y2 = 4 sin(244πt) இச்சமன்பாடுகளை, பொதுச்சமன்பாடு 

y = A sin(2π f1t), உடன் ஒப்பிட

2πf1 = 240π ⇒ f1 = 120Hz

2πf2 = 244π ⇒ f2 = 122Hz

ஒரு வினாடியில் ஏற்படும் விம்மல்களின் எண்ணிக்கை 

| f1 − f2| = |120 − 122| = |− 2| =2 விம்மல்கள்/வினாடி (beats/sec)