தசம எண்கள் மீதான செயல்பாடுகள்

தசம எண்கள் மீதான செயல்பாடுகள்

தசம எண்களைப் பற்றி நாம் ஏற்கனவே கற்றறிந்தோம். மேலும், தசம எண்களைப் பின்னமாக மாற்றவும், அதன் இடமதிப்பு குறித்தும் நாம் கற்றோம். இங்கு, நாம் தசம எண்கள் மீதான நான்கு அடிப்படைச் செயல்பாடுகள் குறித்துக் கற்போம். 

தசம எண்களின் கூட்டலும் கழித்தலும்

இனியா நோட்டுப் புத்தகத்தை ₹46.50 இக்கும், பென்சில் பெட்டியை ₹16.50 இக்கும் வாங்குகிறார். கடைக்காரரிடம் அவள் ₹100 ஐக் கொடுத்தாள் எனில், அவள் பெறும் மீதித் தொகை எவ்வளவு?

இரு பொருள்களின் விலையினைக் கூட்ட, அவள் கடைக்காரருக்குச் செலுத்த வேண்டிய தொகை நமக்குக் கிடைக்கும்.

நோட்டுப் புத்தகத்தின் விலை ₹46.50 மற்றும் பென்சில் பெட்டியின் விலை ₹16.50

இவ்விரு தொகையையும் கூட்டிச் செலுத்த வேண்டிய தொகையினைக் கணக்கிடலாம்.

அவள் பெறும் மீதித் தொகையினைக் கணக்கிட ₹100 இலிருந்து செலுத்திய மொத்தத் தொகையினைக் கழிக்க வேண்டும். மொத்தத் தொகையையும் மீதித் தொகையையும் கணக்கீடு செய்வதன் மூலம் நாம் தசம எண்களின் கூட்டலையும் கழித்தலையும் புரிந்துகொள்ள இயலும்.

மாதிரிகள் மூலம் தசம எண்களின் கூட்டல் மற்றும் கழித்தல்

தசம எண்கள் மீதான கூட்டல் மற்றும் கழித்தலானது தசம அட்டவணை அல்லது பரப்பளவு முறையைப் பயன்படுத்துவதன் மூலம் புரிந்துகொள்ள இயலும்.

i) அட்டவணை முறை:

கீழ்க்காணும் அட்டவணைகள் 1.0, 0.1 மற்றும் 0.01 என்ற தசம எண்களைக் குறிக்கின்றது.

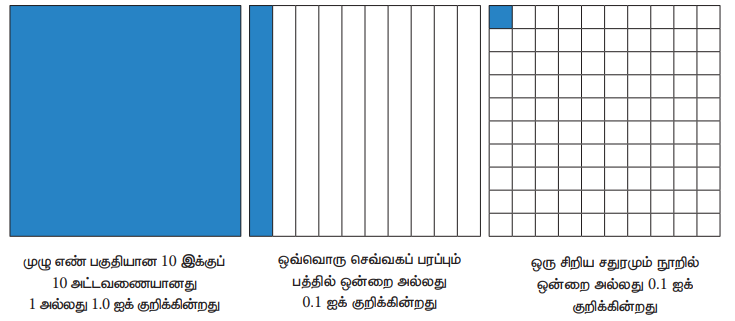
முழு எண் பகுதியான 10 இக்குப் 10 அட்டவணையானது 1 அல்லது 1.0 ஐக் குறிக்கின்றது

ஒவ்வொரு செவ்வகப் பரப்பும் பத்தில் ஒன்றை அல்லது 0.1 ஐக் குறிக்கின்றது

ஒரு சிறிய சதுரமும் நூறில் ஒன்றை அல்லது 0.1 ஐக் குறிக்கின்றது

இந்த அட்டவணைகளைப் பயன்படுத்தித் தசம எண்கள் மீதான கூட்டல் மற்றும் கழித்தல் செயல்பாடுகளை முயல்வோம்.

எடுத்துக்காட்டு 1.5   

0.16 மற்றும் 0.77 ஐக் தசம அட்டவணை முறையைப் பயன்படுத்திக் கூட்டுக.

தீர்வு

இங்கு 0.16=16/100, 0.77=77/100

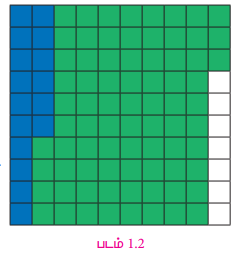
முதலில் 0.16 பகுதியையும், பிறகு 0.77 பகுதியையும் நிழலிடுக.

எனவே,

0.16 + 0.77 = 0.93 ஆகும்.

எடுத்துக்காட்டு 1.6  

0.52 - 0.08 என்பதைத் தசம அட்டவணை முறையைப் பயன்படுத்திக் கண்டறிக.

தீர்வு

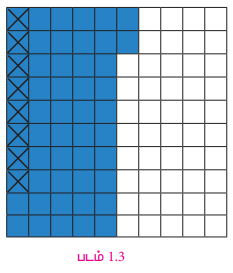
இங்கு , 0.52= 52/100, 0.08=8/100 ஆகும். 0.52 என்ற பகுதியை முதலில் வண்ணத்தால் நிரப்புக. பிறகு 0.08, அதாவது 8/100 என்ற பகுதியை நிரப்பிய பகுதியில் குறுக்குக் கோடு இடுக. குறுக்குக் கோடு இடாத பகுதியே மீதமாகும். அதாவது, 0.52 - 0.08 = 0.44

எடுத்துக்காட்டு 1.7     

தசம அட்டவணை முறையில் 0.72 – 0.51 இன் மதிப்பைக் காண்க.

தீர்வு

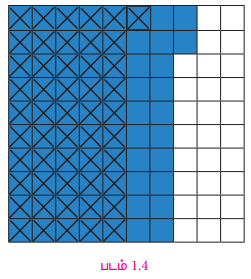
100 கட்டங்கள் உள்ள சதுரத்தைக் கருதுக. அவற்றுள் 72 கட்டங்களை நிழலிடுக. இது 0.72 ஐக் குறிக்கிறது.

பிறகு இந்த 72 நிழலிட்ட கட்டங்களில், 52 கட்டங்களுக்குக் குறுக்குக் கோடு இடுக. இது 0.72 இலிருந்து 0.51 ஐக் கழிப்பதைக் குறிக்கிறது. மீதமுள்ள நிழலிட்டப் பகுதியே தேவையான மதிப்பாகும்.

எனவே , 0.72 – 0.51 = 0.21

இவற்றை முயல்க

கீழ்க்கண்டவற்றினை அட்டவணை முறை மூலம் கண்டறிக:

(i) 0.83 + 0.04 

தீர்வு :

0.83= 83/100 மற்றும்  0.04 = 4/100

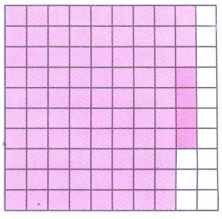
பகுதிகளை நிழலிடுதல் 

0.83 மற்றும்  0.04

நிழலிடப்பட்ட மொத்த பகுதி .

S = 0.83 + 0.04 = 0.87

(ii) 0.35 – 0.09

தீர்வு :

0.35 = 35/100 மற்றும்  0.09 = 9/100

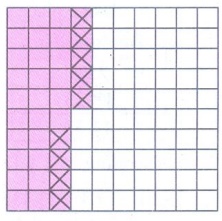
Shading the regions 0.35 by shading 35 boxes out of 100. Striking off 9 boxes out of 35 shaded boxes to subtract 0.09 from 0.35.

The left over shaded boxes represent the required value.

0.35 - 0.09 = 0.26

(ii) பரப்பளவு முறை

தசம எண்களின் முழு எண் பகுதி என்பது ஒரு சதுரப் பரப்பு ஆகும். மேலும், சதுரத்தில் 1/10 ஆவது பாகம் என்பது மெல்லிய செவ்வக வடிவப் பகுதியையும் அதாவது பத்தில் ஒரு தசமப் பகுதி (0.1) யையும், மேலும் செவ்வக வடிவத்தில் 1/100 ஆவது பகுதியானது நூறில் ஒன்றாம் இடத்தையும் (0.01) குறிக்கிறது.  இதேபோன்று மற்ற தசம எண் பகுதிகளையும் குறிக்கலாம்.

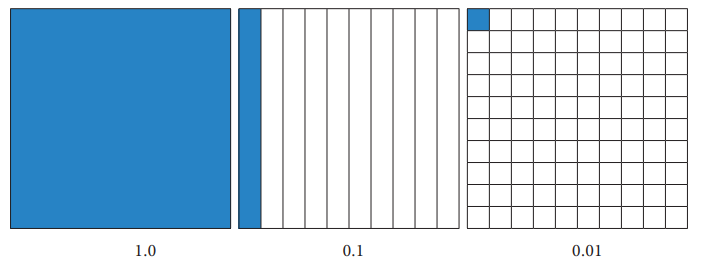
சதுரம் மற்றும் செவ்வகப் பரப்புகளைப் பயன்படுத்தித் தசம எண்களின் கூட்டலையும் கழித்தலையும் செய்வதற்கு முயற்சிக்கலாம்.

எடுத்துக்காட்டு 1.8

3.2 + 6.4 இன் மதிப்பைக் காண்க.

தீர்வு

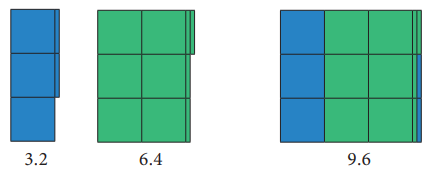
இங்கு 3.2 என்பது நீல வண்ணமாகவும், 6.4 என்பது பச்சை வண்ணமாகவும் குறிப்பிடப்பட்டுள்ளது. எனவே, 3.2 + 6.4 =9.6 ஆகும்.

எடுத்துக்காட்டு 1.9

7.5 – 3.4 இன் மதிப்பைக் காண்க.

தீர்வு

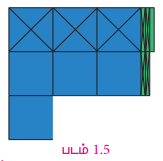
தசம எண் 7.5 என்பது 7 சதுரங்களையும், 5 செவ்வகப் பட்டைகளையும் குறிக்கின்றது. இவற்றில் 7 சதுரங்களிலிருந்து 3 சதுரங்களையும், 5 செவ்வகப் பட்டைகளிலிருந்து 4 செவ்வகப் பட்டைகளையும் குறுக்குக் கோடிட்ட பிறகு மீதம் இருப்பது 4.1 ஆகும்.

இவற்றை முயல்க

பரப்பளவு முறையைப் பயன்படுத்திக் கீழ்க்கண்டவற்றினைத் தீர்க்க.

(i) 1.2 + 3.5 

தீர்வு : 

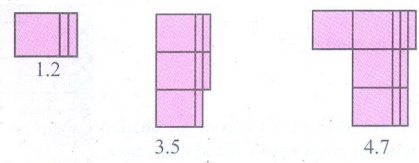
இங்கே 1.2 நீல நிறத்தையும் 3.5 பச்சை நிறத்தையும் குறிக்கின்றது.  எனவே 1.2 மற்றும்  3.5 ஆகியவற்றின் கூட்டுத்தொகை 

 4.7 ஆகும் 

(ii) 3.5 – 2.3

தீர்வு :

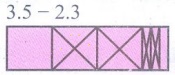
தசம எண் 3.5 என்பது 3 சதுரங்களையும் 5 செவ்வக பட்டைகளையும் குறிக்கின்றது. இவற்றில் 3 சதுரங்களிலிருந்து  

2 சதுரங்களையும் 5 செவ்வக பட்டைகளிலிருந்து 3 செவ்வக பட்டைகளையும் குறுக்கு கோடிட்ட பிறகு மீதம் இருப்பது 1.2 ஆகும் . 

எனவே  3.5 - 2.3 = 1.2.

(iii) இடமதிப்பு அட்டவணை முறை

இதுவரை அட்டவணை மாதிரிகளைப் பயன்படுத்தி, தசம எண்களின் கூட்டலையும் கழித்தலையும் கற்றோம். முன் வகுப்புகளில், தசம எண்களை இடமதிப்பு அட்டவணையில் குறிப்பது பற்றிக் கற்றிருக்கிறோம். அதே இடமதிப்பு அட்டவணையைப் பயன்படுத்தி தசம எண்களின் கூட்டலையும் கழித்தலையும் செய்வது பற்றிப் பார்ப்போம்.

உதாரணமாக, 4.38 மற்றும் 1.67 ஐக் கூட்டப் பின்வருமாறு கிடைக்கிறது.

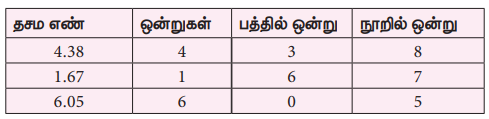
எனவே, 4.38 + 1.67 = 6.05 

எடுத்துக்காட்டு 1.10 

கீழ்க்கண்டவற்றைக் கூட்டுக:

(i) 30.9 + 52.73 (ii) 25.67+33.856 

தீர்வு

(i) 30.9 + 52.73 

இடமதிப்பு அட்டவணையைப் பயன்படுத்துக.

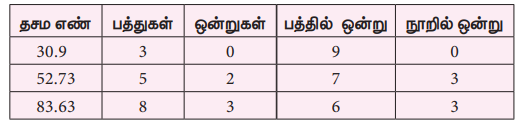
(52.73 இல் உள்ள தசம இலக்கங்களின்  எண்ணிக்கை 2 ஆகும்.  ஆனால், 30.9 இல் உள்ள தசம இலக்கம் 1 மட்டும்தான். எனவே, நூறில் ஒன்றாம் இலக்க மதிப்பாக 0 ஐச் சேர்த்து,  30.9 இன் தசம இலக்கத்தயையும் 2 ஆக எழுத வேண்டும்). 

எனவே , 30.9 + 52.73 = 83.63

(ii) 25.67 + 33.856

இடமதிப்பு அட்டவணையைப் பயன்படுத்துக.

எனவே, 25.67 + 33.856 = 59.526

குறிப்பு 

தசம இலக்கங்களின் வலதுபுறம் 0 ஐச் சேர்ப்பதனால் அந்த எண்ணின் மதிப்பு மாறாது.

எடுத்துக்காட்டு 1.11

தினந்தோறும் மலர் 1.820 கி.மீட்டரை பேருந்திலும், 295 மீட்டரை நடந்தும் பள்ளியை அடைகிறாள். வீட்டிலிருந்து பள்ளியின் தூரத்தினைக் கி.மீட்டரில் கண்டறிக.

தீர்வு

பேருந்தில் கடந்த தொலைவு   = 1.820 கி.மீ

நடந்து கடந்த தொலைவு     = 0.295 கி.மீ

மொத்தத் தொலைவு = 1.820 + 0.295

= 2.115 கி.மீ 

எனவே, வீட்டிலிருந்து பள்ளியானது 2.115 கி.மீ தூரத்திலுள்ளது.

1000 மீ=1 கி.மீ;  1 மீ = 1/1000 கி.மீ

எனவே , 295 மீ = 295/1000 கி.மீ

= 0.295 கி.மீ

எடுத்துக்காட்டு 1.12 

4.97 இலிருந்து 2.85 ஐக் கழிக்கவும்.

தீர்வு

4.97 – 2.85 = ? 

இடமதிப்பு அட்டவணையைப் பயன்படுத்துக.

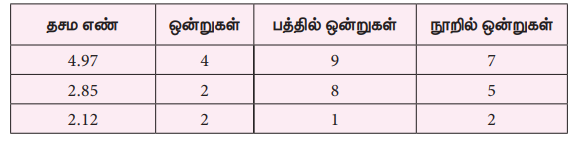
எனவே, 4.97 – 2.85 = 2.12

எடுத்துக்காட்டு 1.13 

12.7 இலிருந்து 3.09 ஐக் கழிக்கவும்.

தீர்வு

12.7 - 3.09 = ? 

இடமதிப்பு அட்டவணையைப் பயன்படுத்துக.

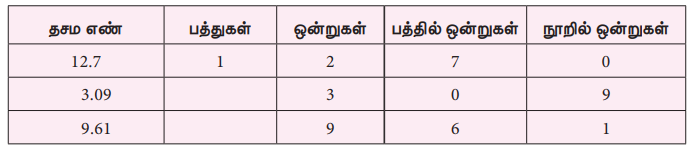
எனவே, 12.7 - 3.09 = 9.61

குறிப்பு 

1. தசம இலக்கங்களைச் சமன்படுத்த இலக்கங்களின் வலதுபுற முடிவில் 0 ஐச் சேர்க்கலாம். 

2. தசம இலக்கங்களின் வலப்புற இறுதியில் சேர்க்கப்படும் பூச்சியம், தசம எண்களைக் கூட்டவோ அல்லது கழிக்கவோ உதவும்.

எடுத்துக்காட்டு 1.14

86.9 இலிருந்து 32.042 ஐக் கழிக்கவும்.

தீர்வு

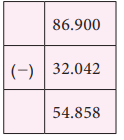
எனவே,     86.9 - 32.042 = 54.858

இவற்றை முயல்க 

நிரல், நிறை மற்றும் மூலை விட்டங்களின் கூடுதல் 1.5 என வருமாறு கீழேயுள்ள மாயச்சதுரத்தினை நிரப்புக.

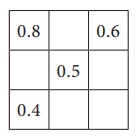
தீர்வு : 

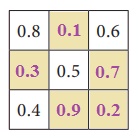
எடுத்துக்காட்டு 1.15 

நரேன் 7.4 கி.கி மாம்பழங்களை வாங்கினார். வீட்டிற்குச் செல்லும் வழியில், 4.650 கி.கி மாம்பழங்களைத் தனது சகோதரிக்கு அளித்துவிட்டார். அவரிடம் மீதமுள்ள மாம்பழங்களின் எடையைக் கண்டறிக.

தீர்வு

நரேன் வாங்கிய மாம்பழங்கள் = 7.4 கி.கி 

நரேன் தனது சகோதரிக்கு வழங்கிய மாம்பழங்கள் = 4.650 கி.கி

நரேன் குடும்பத்திற்காகக் கொண்டு சென்ற மீதமுள்ள மாம்பழங்களின் எடை = 7.400 - 4.650 கி.கி. 

     = 2.750 

எனவே, மீதமுள்ள மாம்பழங்களின் எடை 2.750 கி.கி ஆகும்.

நாம் அன்றாட வாழ்வில் பணப்பரிமாற்றம், எடை, நீளங்களை அளத்தல், முதலானவற்றில் தசம எண்களைப் பயன்படுத்துகிறோம். மிகத் துல்லியமாக அளவீடு தேவைப்படும்போது நாம் தசம எண்களைப் பயன்படுத்துகிறோம்.